Eigen中三维位姿表示方式以及相互转换

89 阅读 0 评论 59 点赞

我是靠谱客的博主花痴指甲油，这篇文章主要介绍Eigen中三维位姿表示方式以及相互转换，现在分享给大家，希望可以做个参考。

目前三维位姿表示方式主要有旋转矩阵、欧拉角、轴角、四元数等，Eigen库中提供了四元数、欧拉角、旋转矩阵的转换方法：

Eigen旋转的表示方式与相互转换

复制代码

#include <iostream>
    #include <Eigen/Core>
    #include <Eigen/Geometry>
    using namespace std;
    #define PI (3.1415926535897932346f)
    int main(int argc, char **argv) 
    {
        /**** 1. 旋转向量 ****/
        cout << endl << "********** AngleAxis **********" << endl;
        //1.0 初始化旋转向量,沿Z轴旋转45度的旋转向量
        Eigen::AngleAxisd rotation_vector1 (M_PI/4, Eigen::Vector3d(0, 0, 1)); 
        //1.1 旋转向量转换为旋转矩阵
        //旋转向量用matrix()转换成旋转矩阵
        Eigen::Matrix3d rotation_matrix1 = Eigen::Matrix3d::Identity();
        rotation_matrix1 = rotation_vector1.matrix();
        cout << "rotation matrix1 =n" << rotation_matrix1 << endl;                
        //或者由罗德里格公式进行转换
        rotation_matrix1 = rotation_vector1.toRotationMatrix();
        cout << "rotation matrix1 =n" << rotation_matrix1 << endl; 
        /*1.2 旋转向量转换为欧拉角*/
        //将旋转向量转换为旋转矩阵,再由旋转矩阵转换为欧拉角,详见旋转矩阵转换为欧拉角
        Eigen::Vector3d eulerAngle1 = rotation_vector1.matrix().eulerAngles(2,1,0);
        cout << "eulerAngle1, z y x: " << eulerAngle1 << endl;
        /*1.3 旋转向量转四元数*/
        Eigen::Quaterniond quaternion1(rotation_vector1);
        //或者
        Eigen::Quaterniond quaternion1_1;
        quaternion1_1 = rotation_vector1;
        cout << "quaternion1 x: " << quaternion1.x() << endl;
        cout << "quaternion1 y: " << quaternion1.y() << endl;
        cout << "quaternion1 z: " << quaternion1.z() << endl;
        cout << "quaternion1 w: " << quaternion1.w() << endl;
        cout << "quaternion1_1 x: " << quaternion1_1.x() << endl;
        cout << "quaternion1_1 y: " << quaternion1_1.y() << endl;
        cout << "quaternion1_1 z: " << quaternion1_1.z() << endl;
        cout << "quaternion1_1 w: " << quaternion1_1.w() << endl;
        /**** 2. 旋转矩阵 *****/
        cout << endl << "********** RotationMatrix **********" << endl;
        //2.0 旋转矩阵初始化
        Eigen::Matrix3d rotation_matrix2;
        rotation_matrix2 << 0.707107, -0.707107, 0, 0.707107, 0.707107, 0, 0, 0, 1;
    ;
        //或直接单位矩阵初始化
        Eigen::Matrix3d rotation_matrix2_1 = Eigen::Matrix3d::Identity();
        //2.1 旋转矩阵转换为欧拉角
        //ZYX顺序，即先绕x轴roll,再绕y轴pitch,最后绕z轴yaw,0表示X轴,1表示Y轴,2表示Z轴
        Eigen::Vector3d euler_angles = rotation_matrix2.eulerAngles(2, 1, 0); 
        cout << "yaw(z) pitch(y) roll(x) = " << euler_angles.transpose() << endl;
        //2.2 旋转矩阵转换为旋转向量
        Eigen::AngleAxisd rotation_vector2;
        rotation_vector2.fromRotationMatrix(rotation_matrix2);
        //或者
        Eigen::AngleAxisd rotation_vector2_1(rotation_matrix2);
        cout << "rotation_vector2 " << "angle is: " << rotation_vector2.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector2.axis().transpose() << endl;
        cout << "rotation_vector2_1 " << "angle is: " << rotation_vector2_1.angle() * (180 / M_PI) 
                                      << " axis is: " << rotation_vector2_1.axis().transpose() << endl;
        //2.3 旋转矩阵转换为四元数
        Eigen::Quaterniond quaternion2(rotation_matrix2);
        //或者
        Eigen::Quaterniond quaternion2_1;
        quaternion2_1 = rotation_matrix2;
        cout << "quaternion2 x: " << quaternion2.x() << endl;
        cout << "quaternion2 y: " << quaternion2.y() << endl;
        cout << "quaternion2 z: " << quaternion2.z() << endl;
        cout << "quaternion2 w: " << quaternion2.w() << endl;
        cout << "quaternion2_1 x: " << quaternion2_1.x() << endl;
        cout << "quaternion2_1 y: " << quaternion2_1.y() << endl;
        cout << "quaternion2_1 z: " << quaternion2_1.z() << endl;
        cout << "quaternion2_1 w: " << quaternion2_1.w() << endl;
        /**** 3. 欧拉角 ****/
        cout << endl << "********** EulerAngle **********" << endl;
        //3.0 初始化欧拉角(Z-Y-X，即RPY, 先绕x轴roll,再绕y轴pitch,最后绕z轴yaw)
        Eigen::Vector3d ea(0.785398, -0, 0);
        //3.1 欧拉角转换为旋转矩阵
        Eigen::Matrix3d rotation_matrix3;
        rotation_matrix3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                           Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                           Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());
        cout << "rotation matrix3 =n" << rotation_matrix3 << endl;   
        //3.2 欧拉角转换为四元数,
        Eigen::Quaterniond quaternion3;
        quaternion3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                      Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                      Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());
        cout << "quaternion3 x: " << quaternion3.x() << endl;
        cout << "quaternion3 y: " << quaternion3.y() << endl;
        cout << "quaternion3 z: " << quaternion3.z() << endl;
        cout << "quaternion3 w: " << quaternion3.w() << endl;
        //3.3 欧拉角转换为旋转向量
        Eigen::AngleAxisd rotation_vector3;
        rotation_vector3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                           Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                           Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());  
        cout << "rotation_vector3 " << "angle is: " << rotation_vector3.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector3.axis().transpose() << endl;
        /**** 4.四元数 ****/
        cout << endl << "********** Quaternion **********" << endl;
        //4.0 初始化四元素,注意eigen Quaterniond类四元数初始化参数顺序为w,x,y,z
        Eigen::Quaterniond quaternion4(0.92388, 0, 0, 0.382683);
        //4.1 四元数转换为旋转向量
        Eigen::AngleAxisd rotation_vector4(quaternion4);
        //或者
        Eigen::AngleAxisd rotation_vector4_1;
        rotation_vector4_1 = quaternion4;
        cout << "rotation_vector4 " << "angle is: " << rotation_vector4.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector4.axis().transpose() << endl;
        cout << "rotation_vector4_1 " << "angle is: " << rotation_vector4_1.angle() * (180 / M_PI) 
                                      << " axis is: " << rotation_vector4_1.axis().transpose() << endl;
        //4.2 四元数转换为旋转矩阵
        Eigen::Matrix3d rotation_matrix4;
        rotation_matrix4 = quaternion4.matrix();
        Eigen::Matrix3d rotation_matrix4_1;
        rotation_matrix4_1 = quaternion4.toRotationMatrix();
        cout << "rotation matrix4 =n" << rotation_matrix4 << endl;
        cout << "rotation matrix4_1 =n" << rotation_matrix4_1 << endl;      
        //4.4 四元数转欧拉角(Z-Y-X，即RPY)
        Eigen::Vector3d eulerAngle4 = quaternion4.matrix().eulerAngles(2,1,0);
        cout << "yaw(z) pitch(y) roll(x) = " << eulerAngle4.transpose() << endl;
        return 0;
    }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
    #include <iostream>
    #include <Eigen/Core>
    #include <Eigen/Geometry>
    using namespace std;
    #define PI (3.1415926535897932346f)
    int main(int argc, char **argv) 
    {
        /**** 1. 旋转向量 ****/
        cout << endl << "********** AngleAxis **********" << endl;
        //1.0 初始化旋转向量,沿Z轴旋转45度的旋转向量
        Eigen::AngleAxisd rotation_vector1 (M_PI/4, Eigen::Vector3d(0, 0, 1)); 
        //1.1 旋转向量转换为旋转矩阵
        //旋转向量用matrix()转换成旋转矩阵
        Eigen::Matrix3d rotation_matrix1 = Eigen::Matrix3d::Identity();
        rotation_matrix1 = rotation_vector1.matrix();
        cout << "rotation matrix1 =n" << rotation_matrix1 << endl;                
        //或者由罗德里格公式进行转换
        rotation_matrix1 = rotation_vector1.toRotationMatrix();
        cout << "rotation matrix1 =n" << rotation_matrix1 << endl; 
        /*1.2 旋转向量转换为欧拉角*/
        //将旋转向量转换为旋转矩阵,再由旋转矩阵转换为欧拉角,详见旋转矩阵转换为欧拉角
        Eigen::Vector3d eulerAngle1 = rotation_vector1.matrix().eulerAngles(2,1,0);
        cout << "eulerAngle1, z y x: " << eulerAngle1 << endl;
        /*1.3 旋转向量转四元数*/
        Eigen::Quaterniond quaternion1(rotation_vector1);
        //或者
        Eigen::Quaterniond quaternion1_1;
        quaternion1_1 = rotation_vector1;
        cout << "quaternion1 x: " << quaternion1.x() << endl;
        cout << "quaternion1 y: " << quaternion1.y() << endl;
        cout << "quaternion1 z: " << quaternion1.z() << endl;
        cout << "quaternion1 w: " << quaternion1.w() << endl;
        cout << "quaternion1_1 x: " << quaternion1_1.x() << endl;
        cout << "quaternion1_1 y: " << quaternion1_1.y() << endl;
        cout << "quaternion1_1 z: " << quaternion1_1.z() << endl;
        cout << "quaternion1_1 w: " << quaternion1_1.w() << endl;
        /**** 2. 旋转矩阵 *****/
        cout << endl << "********** RotationMatrix **********" << endl;
        //2.0 旋转矩阵初始化
        Eigen::Matrix3d rotation_matrix2;
        rotation_matrix2 << 0.707107, -0.707107, 0, 0.707107, 0.707107, 0, 0, 0, 1;
    ;
        //或直接单位矩阵初始化
        Eigen::Matrix3d rotation_matrix2_1 = Eigen::Matrix3d::Identity();
        //2.1 旋转矩阵转换为欧拉角
        //ZYX顺序，即先绕x轴roll,再绕y轴pitch,最后绕z轴yaw,0表示X轴,1表示Y轴,2表示Z轴
        Eigen::Vector3d euler_angles = rotation_matrix2.eulerAngles(2, 1, 0); 
        cout << "yaw(z) pitch(y) roll(x) = " << euler_angles.transpose() << endl;
        //2.2 旋转矩阵转换为旋转向量
        Eigen::AngleAxisd rotation_vector2;
        rotation_vector2.fromRotationMatrix(rotation_matrix2);
        //或者
        Eigen::AngleAxisd rotation_vector2_1(rotation_matrix2);
        cout << "rotation_vector2 " << "angle is: " << rotation_vector2.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector2.axis().transpose() << endl;
        cout << "rotation_vector2_1 " << "angle is: " << rotation_vector2_1.angle() * (180 / M_PI) 
                                      << " axis is: " << rotation_vector2_1.axis().transpose() << endl;
        //2.3 旋转矩阵转换为四元数
        Eigen::Quaterniond quaternion2(rotation_matrix2);
        //或者
        Eigen::Quaterniond quaternion2_1;
        quaternion2_1 = rotation_matrix2;
        cout << "quaternion2 x: " << quaternion2.x() << endl;
        cout << "quaternion2 y: " << quaternion2.y() << endl;
        cout << "quaternion2 z: " << quaternion2.z() << endl;
        cout << "quaternion2 w: " << quaternion2.w() << endl;
        cout << "quaternion2_1 x: " << quaternion2_1.x() << endl;
        cout << "quaternion2_1 y: " << quaternion2_1.y() << endl;
        cout << "quaternion2_1 z: " << quaternion2_1.z() << endl;
        cout << "quaternion2_1 w: " << quaternion2_1.w() << endl;
        /**** 3. 欧拉角 ****/
        cout << endl << "********** EulerAngle **********" << endl;
        //3.0 初始化欧拉角(Z-Y-X，即RPY, 先绕x轴roll,再绕y轴pitch,最后绕z轴yaw)
        Eigen::Vector3d ea(0.785398, -0, 0);
        //3.1 欧拉角转换为旋转矩阵
        Eigen::Matrix3d rotation_matrix3;
        rotation_matrix3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                           Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                           Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());
        cout << "rotation matrix3 =n" << rotation_matrix3 << endl;   
        //3.2 欧拉角转换为四元数,
        Eigen::Quaterniond quaternion3;
        quaternion3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                      Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                      Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());
        cout << "quaternion3 x: " << quaternion3.x() << endl;
        cout << "quaternion3 y: " << quaternion3.y() << endl;
        cout << "quaternion3 z: " << quaternion3.z() << endl;
        cout << "quaternion3 w: " << quaternion3.w() << endl;
        //3.3 欧拉角转换为旋转向量
        Eigen::AngleAxisd rotation_vector3;
        rotation_vector3 = Eigen::AngleAxisd(ea[0], Eigen::Vector3d::UnitZ()) * 
                           Eigen::AngleAxisd(ea[1], Eigen::Vector3d::UnitY()) * 
                           Eigen::AngleAxisd(ea[2], Eigen::Vector3d::UnitX());  
        cout << "rotation_vector3 " << "angle is: " << rotation_vector3.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector3.axis().transpose() << endl;
        /**** 4.四元数 ****/
        cout << endl << "********** Quaternion **********" << endl;
        //4.0 初始化四元素,注意eigen Quaterniond类四元数初始化参数顺序为w,x,y,z
        Eigen::Quaterniond quaternion4(0.92388, 0, 0, 0.382683);
        //4.1 四元数转换为旋转向量
        Eigen::AngleAxisd rotation_vector4(quaternion4);
        //或者
        Eigen::AngleAxisd rotation_vector4_1;
        rotation_vector4_1 = quaternion4;
        cout << "rotation_vector4 " << "angle is: " << rotation_vector4.angle() * (180 / M_PI) 
                                    << " axis is: " << rotation_vector4.axis().transpose() << endl;
        cout << "rotation_vector4_1 " << "angle is: " << rotation_vector4_1.angle() * (180 / M_PI) 
                                      << " axis is: " << rotation_vector4_1.axis().transpose() << endl;
        //4.2 四元数转换为旋转矩阵
        Eigen::Matrix3d rotation_matrix4;
        rotation_matrix4 = quaternion4.matrix();
        Eigen::Matrix3d rotation_matrix4_1;
        rotation_matrix4_1 = quaternion4.toRotationMatrix();
        cout << "rotation matrix4 =n" << rotation_matrix4 << endl;
        cout << "rotation matrix4_1 =n" << rotation_matrix4_1 << endl;      
        //4.4 四元数转欧拉角(Z-Y-X，即RPY)
        Eigen::Vector3d eulerAngle4 = quaternion4.matrix().eulerAngles(2,1,0);
        cout << "yaw(z) pitch(y) roll(x) = " << eulerAngle4.transpose() << endl;
        return 0;
    }

输出：
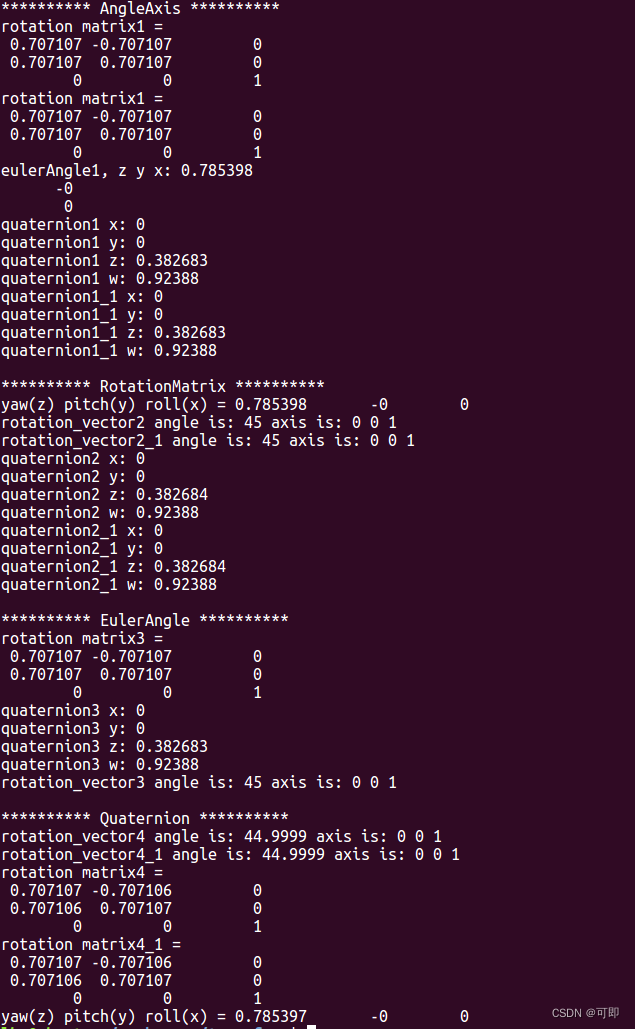
在这里插入图片描述
或

复制代码

#include <iostream>
#include <Eigen/Eigen>
#include <stdlib.h>
#include <Eigen/Geometry>
#include <Eigen/Core>
#include <vector>
#include <math.h>
 
using namespace std;
using namespace Eigen;
 
Eigen::Quaterniond euler2Quaternion(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
 
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    cout << "Euler2Quaternion result is:" <<endl;
    cout << "x = " << q.x() <<endl;
    cout << "y = " << q.y() <<endl;
    cout << "z = " << q.z() <<endl;
    cout << "w = " << q.w() <<endl<<endl;
    return q;
}
Eigen::Vector3d Quaterniond2Euler(const double x,const double y,const double z,const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Vector3d euler = q.toRotationMatrix().eulerAngles(2, 1, 0);
    cout << "Quaterniond2Euler result is:" <<endl;
    cout << "z = "<< euler[2] << endl ;
    cout << "y = "<< euler[1] << endl ;
    cout << "x = "<< euler[0] << endl << endl;
}
Eigen::Matrix3d Quaternion2RotationMatrix(const double x,const double y,const double z,const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Matrix3d R = q.normalized().toRotationMatrix();
    cout << "Quaternion2RotationMatrix result is:" <<endl;
    cout << "R = " << endl << R << endl<< endl;
    return R;
}
Eigen::Quaterniond rotationMatrix2Quaterniond(Eigen::Matrix3d R)
{
    Eigen::Quaterniond q = Eigen::Quaterniond(R);
    q.normalize();
    cout << "RotationMatrix2Quaterniond result is:" <<endl;
    cout << "x = " << q.x() <<endl;
    cout << "y = " << q.y() <<endl;
    cout << "z = " << q.z() <<endl;
    cout << "w = " << q.w() <<endl<<endl;
    return q;
}
Eigen::Matrix3d euler2RotationMatrix(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    Eigen::Matrix3d R = q.matrix();
    cout << "Euler2RotationMatrix result is:" <<endl;
    cout << "R = " << endl << R << endl<<endl;
    return R;
}
Eigen::Vector3d RotationMatrix2euler(Eigen::Matrix3d R)
{
    Eigen::Matrix3d m;
    m = R;
    Eigen::Vector3d euler = m.eulerAngles(0, 1, 2);
    cout << "RotationMatrix2euler result is:" << endl;
    cout << "x = "<< euler[2] << endl ;
    cout << "y = "<< euler[1] << endl ;
    cout << "z = "<< euler[0] << endl << endl;
    return euler;
}
int main(int argc, char **argv)
{
  //example
   Eigen::Vector3d x_axiz,y_axiz,z_axiz;
   x_axiz << 1,0,0;
   y_axiz << 0,1,0;
   z_axiz << 0,0,1;
 
   Eigen::Matrix3d R;
   R << x_axiz,y_axiz,z_axiz;
   rotationMatrix2Quaterniond(R);
   euler2RotationMatrix(0,0,0);
   RotationMatrix2euler(R);
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
#include <iostream>
#include <Eigen/Eigen>
#include <stdlib.h>
#include <Eigen/Geometry>
#include <Eigen/Core>
#include <vector>
#include <math.h>
 
using namespace std;
using namespace Eigen;
 
Eigen::Quaterniond euler2Quaternion(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
 
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    cout << "Euler2Quaternion result is:" <<endl;
    cout << "x = " << q.x() <<endl;
    cout << "y = " << q.y() <<endl;
    cout << "z = " << q.z() <<endl;
    cout << "w = " << q.w() <<endl<<endl;
    return q;
}
Eigen::Vector3d Quaterniond2Euler(const double x,const double y,const double z,const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Vector3d euler = q.toRotationMatrix().eulerAngles(2, 1, 0);
    cout << "Quaterniond2Euler result is:" <<endl;
    cout << "z = "<< euler[2] << endl ;
    cout << "y = "<< euler[1] << endl ;
    cout << "x = "<< euler[0] << endl << endl;
}
Eigen::Matrix3d Quaternion2RotationMatrix(const double x,const double y,const double z,const double w)
{
    Eigen::Quaterniond q;
    q.x() = x;
    q.y() = y;
    q.z() = z;
    q.w() = w;
    Eigen::Matrix3d R = q.normalized().toRotationMatrix();
    cout << "Quaternion2RotationMatrix result is:" <<endl;
    cout << "R = " << endl << R << endl<< endl;
    return R;
}
Eigen::Quaterniond rotationMatrix2Quaterniond(Eigen::Matrix3d R)
{
    Eigen::Quaterniond q = Eigen::Quaterniond(R);
    q.normalize();
    cout << "RotationMatrix2Quaterniond result is:" <<endl;
    cout << "x = " << q.x() <<endl;
    cout << "y = " << q.y() <<endl;
    cout << "z = " << q.z() <<endl;
    cout << "w = " << q.w() <<endl<<endl;
    return q;
}
Eigen::Matrix3d euler2RotationMatrix(const double roll, const double pitch, const double yaw)
{
    Eigen::AngleAxisd rollAngle(roll, Eigen::Vector3d::UnitZ());
    Eigen::AngleAxisd yawAngle(yaw, Eigen::Vector3d::UnitY());
    Eigen::AngleAxisd pitchAngle(pitch, Eigen::Vector3d::UnitX());
    Eigen::Quaterniond q = rollAngle * yawAngle * pitchAngle;
    Eigen::Matrix3d R = q.matrix();
    cout << "Euler2RotationMatrix result is:" <<endl;
    cout << "R = " << endl << R << endl<<endl;
    return R;
}
Eigen::Vector3d RotationMatrix2euler(Eigen::Matrix3d R)
{
    Eigen::Matrix3d m;
    m = R;
    Eigen::Vector3d euler = m.eulerAngles(0, 1, 2);
    cout << "RotationMatrix2euler result is:" << endl;
    cout << "x = "<< euler[2] << endl ;
    cout << "y = "<< euler[1] << endl ;
    cout << "z = "<< euler[0] << endl << endl;
    return euler;
}
int main(int argc, char **argv)
{
  //example
   Eigen::Vector3d x_axiz,y_axiz,z_axiz;
   x_axiz << 1,0,0;
   y_axiz << 0,1,0;
   z_axiz << 0,0,1;
 
   Eigen::Matrix3d R;
   R << x_axiz,y_axiz,z_axiz;
   rotationMatrix2Quaterniond(R);
   euler2RotationMatrix(0,0,0);
   RotationMatrix2euler(R);
}

关于“旋转矩阵、欧拉角、轴角、四元数”之间的联系与思考

在这里插入图片描述

内旋与外旋

更多参考：https://zhuanlan.zhihu.com/p/144032401
在这里插入图片描述

Eigen::eulerAngles(2,1,0) 注意

参考：https://blog.csdn.net/delovsam/article/details/104432185
普通的方法是，用Eigen，把四元数转成旋转矩阵，再从旋转矩阵转到欧拉角：
::Eigen::Quaterniond q(w, x, y, z);
::Eigen::Matrix3d rx = q.toRotationMatrix();
::Eigen::Vector3d ea = rx.eulerAngles(2,1,0);
但这个方法存在问题，即可能转出来的欧拉角，不是想要的，**因为因为同一个四元数，可以用2个欧拉角来表示，而这个方法得到的结果有可能是用转角大于2PI的方式表达的。**例如，四元数(0.00392036, -0.00511095, -0.613622, 0.789573)应当转为欧拉角(-1.32133, -0.00325971, 0.0124636)，但用Eigen却被转成了(1.82026, -3.13833, -3.12913)。

由于无人车在近似平面上运动，因此yaw角可能取值±180°，roll和pitch变化很小才对。但是使用eulerAngles(2,1,0)时，出现roll,pitch达到正负180的现象，明显错误。如下图：
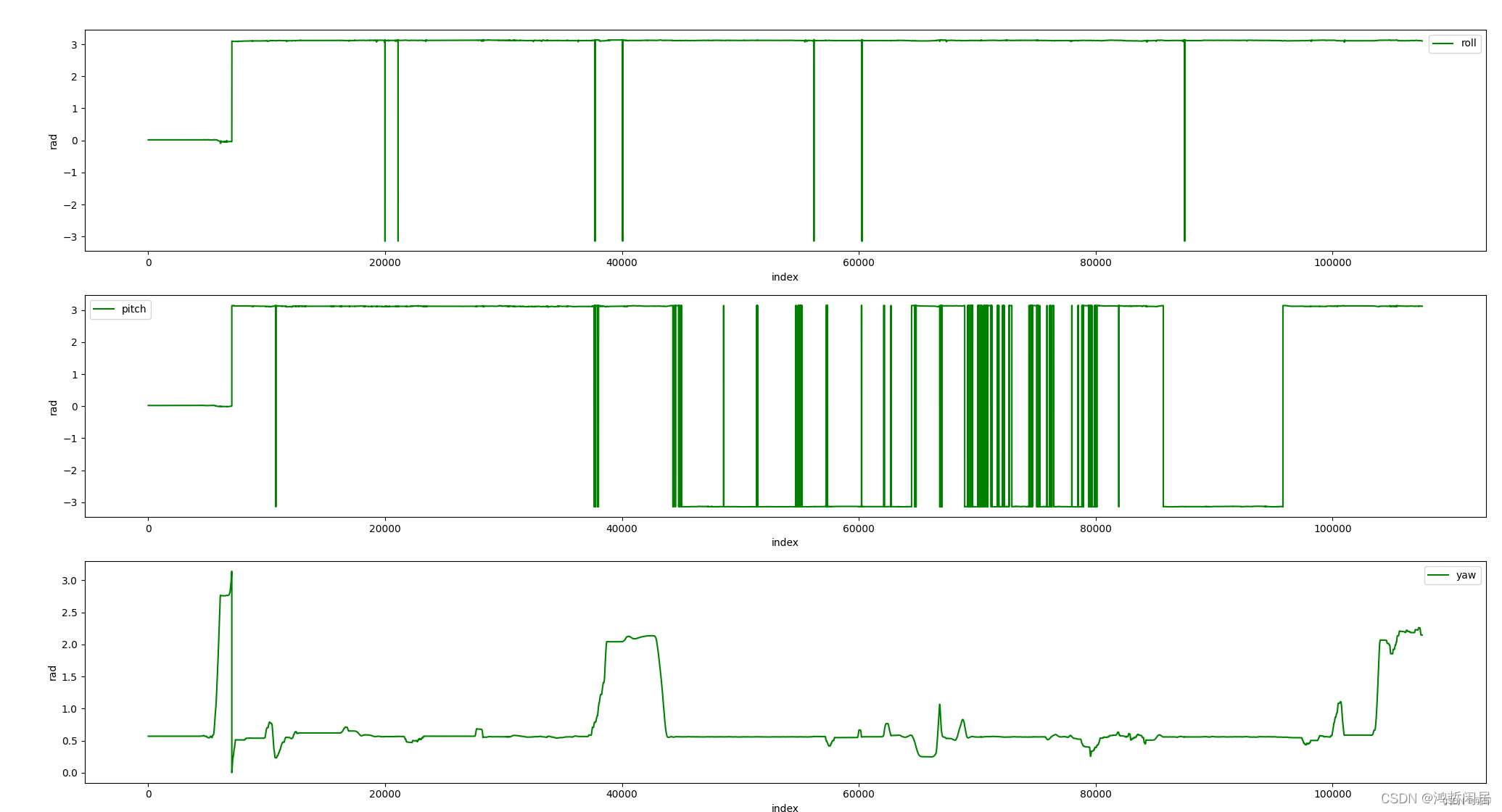在这里插入图片描述为了避免这个问题，有以下解决办法：

方法一

使用 Conversion between quaternions and Euler angles（https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles）中给出的一个算法（如下），这个算法可以保证出来的欧拉角不会超过2PI。

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#define _USE_MATH_DEFINES
#include <cmath>
 
struct Quaternion {
    double w, x, y, z;
};
 
struct EulerAngles {
    double roll, pitch, yaw;
};
 
EulerAngles ToEulerAngles(Quaternion q) {
    EulerAngles angles;
 
    // roll (x-axis rotation)
    double sinr_cosp = 2 * (q.w * q.x + q.y * q.z);
    double cosr_cosp = 1 - 2 * (q.x * q.x + q.y * q.y);
    angles.roll = std::atan2(sinr_cosp, cosr_cosp);
 
    // pitch (y-axis rotation)
    double sinp = 2 * (q.w * q.y - q.z * q.x);
    if (std::abs(sinp) >= 1)
        angles.pitch = std::copysign(M_PI / 2, sinp); // use 90 degrees if out of range
    else
        angles.pitch = std::asin(sinp);
 
    // yaw (z-axis rotation)
    double siny_cosp = 2 * (q.w * q.z + q.x * q.y);
    double cosy_cosp = 1 - 2 * (q.y * q.y + q.z * q.z);
    angles.yaw = std::atan2(siny_cosp, cosy_cosp);
 
    return angles;
}

方法二：
使用pcl::getTranslationAndEulerAngles()。但有的文章测试认为该函数在计算绕Z轴的旋转角时存在精度损失：pcl::getTranslationAndEulerAngles精度缺失问题
但我觉得影响不大，同时LIO-Sam中也是用的这种方式。

复制代码

1
2
3
4
5
6
7
#include <pcl/common/transforms.h>
#include <Eigen/Core>
     
float x, y, z, roll, pitch, yaw;
Eigen::Affine3f tmp(T_utm_lidar.cast<float>());
pcl::getTranslationAndEulerAngles(tmp, x, y, z, roll, pitch, yaw);

使用pcl::getTranslationAndEulerAngles()方法的效果如下：
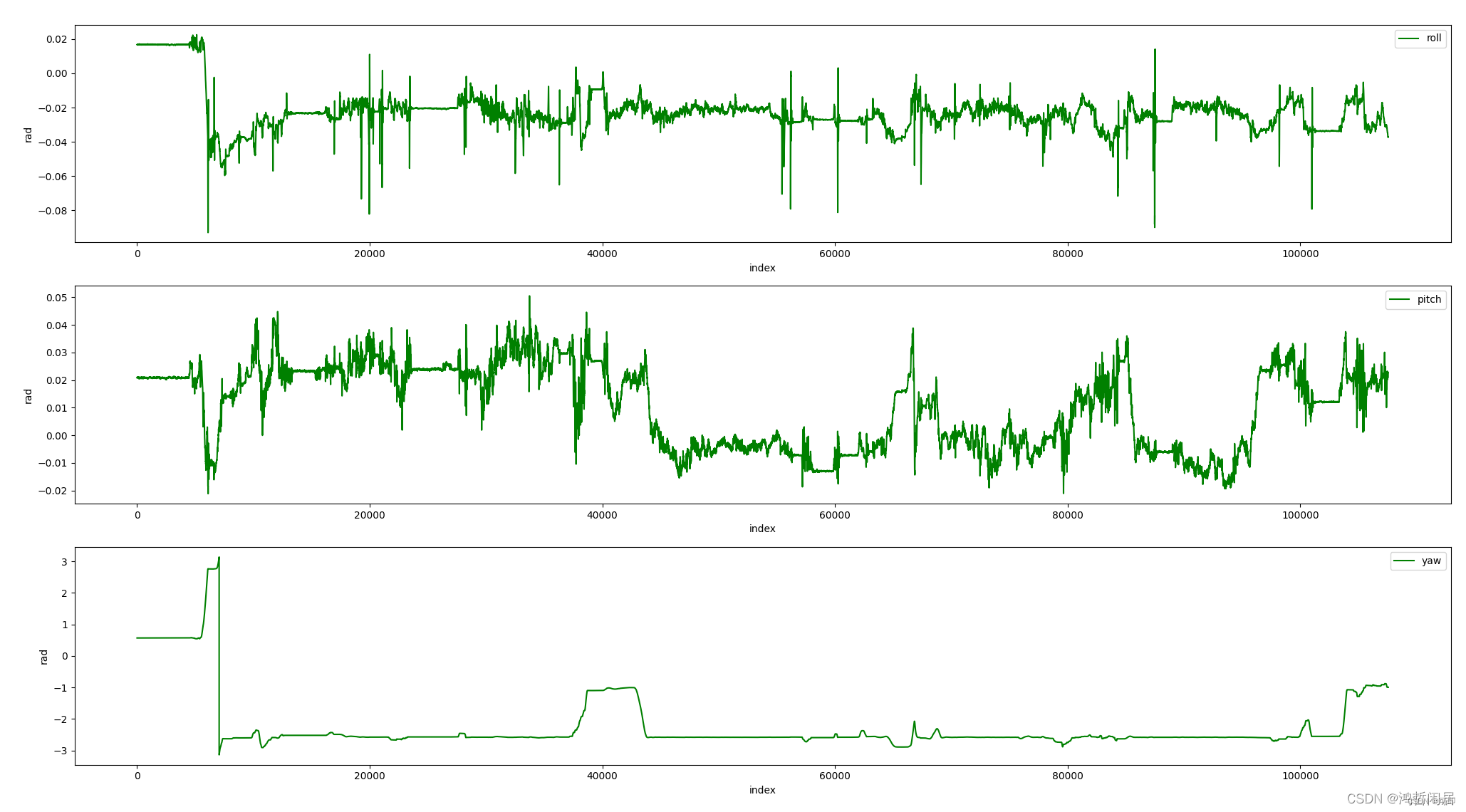
在这里插入图片描述
方法三

可使用vio中R2ypr函数

复制代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

Utility::R2ypr(q.toRotationMatrix())

输出的是：yaw pitch roll 的vector3d向量，单位是度数，（正负180）

Utility::R2ypr得到的yaw，pitch，roll均利用atan2函数故只能输出±180之间，（注意atan2不同atan，后者只能±90）

而.eulerAngles得到的是[0:pi] [-pi:pi] [-pi:pi]，

函数定义：
static Eigen::Vector3d R2ypr(const Eigen::Matrix3d &R)
    {
        Eigen::Vector3d n = R.col(0);
        Eigen::Vector3d o = R.col(1);
        Eigen::Vector3d a = R.col(2);

        Eigen::Vector3d ypr(3);
        double y = atan2(n(1), n(0));
        double p = atan2(-n(2), n(0) * cos(y) + n(1) * sin(y));
        double r = atan2(a(0) * sin(y) - a(1) * cos(y), -o(0) * sin(y) + o(1) * cos(y));
        ypr(0) = y;
        ypr(1) = p;
        ypr(2) = r;

        return ypr / M_PI * 180.0;
    }

感谢：
https://blog.csdn.net/u011906844/article/details/121863578
https://blog.csdn.net/hltt3838/article/details/110262089
http://t.zoukankan.com/long5683-p-14373627.html
…