双线性对的研究以及在分布式系统中的应用

背景介绍

公钥密码体制

1. 基于大整数因子分解困难，如RSA —随着计算能力的增强，要求RSA的密钥长度越来越长
2. 基于离散对数困难问题，如EIGamal密码体制和椭圆曲线密码体制（Elliptiic Curve Cryptosystem，ECC）—ECC密钥长度要求更短，160bit密钥长度的ECC与1024bit的RSA具有相当的安全性。

ECC具备密钥量小，安全性高，灵活性好和易于硬件实现的特点。其上的双线性对是构造加密，签名方案的重要工具，如：代数曲线上的Weil Pairing和Tate Pairing。

双线性对（Bilinear Pairing）

截图取自《基于双线性对的分布式密码系统与应用研究》田有亮

分布式密码技术

1. 知识承诺

分类

1. 计算隐藏，完备绑定的比特承诺方案
2. 完备隐藏，计算绑定的比特承诺方案

Pedersen的知识承诺方案

1. 初始化：假设g，h是群 $G_n$（n为素数）中的两个生成元，$lo{g}_{g}h$是未知的，即计算离散对数不可行；
2. 承诺阶段：为了承诺整数$a\in Z_n$，发送者在$Z_n$中随机选择数 r，计算a的承诺$$C(a,r)=g^a{h}^r$$
3. 公布阶段：发送者发送a, r给接收者，接收者计算$g^a{h}^r$，判断结果是否等于$C(a,r)$，若相等则正确揭开承诺，否则拒绝承诺。

2. 秘密共享

目的

1. 实现权力分散以避免滥用职权；
2. 即使失去了部分子秘密，也不会影响到秘密信息的恢复。

方案

1. 集中环境下-支持多播通信的组密钥管理协议
2. 集中式密钥分发中心
3. 分布式密钥分发中心（将单个服务器的任务分配给一组服务器）
4. 可验证秘密分享和知识的非交互零知识证明

内容

1979年Shamir和Blakley分别提出了秘密共享机制，即将敏感信息（如密钥）分发给团队中的成员进行管理，以分散加/解密权力，签名权力和验证权力。秘密共享方案是一种分发，保存和恢复秘密信息的方法，是研究如何在一组参与者之间分配或共享一个秘密信息，而该共享秘密信息只有在规定数量的授权用户共同参与才能用特定的方法恢复。若一个秘密共享方案中每个非授权集都不能得到该秘密的任何有用信息，则称其为完美秘密共享(Perfect Secret Sharing)。

分类

可验证秘密共享(Verifiable Secret Sharing, VSS)

可公开验证秘密共享(Publicly Verifiable Secret Sharing, PVSS)

先应式秘密共享(Proactive Verifiable Secret Sharing，PSS)

在线秘密共享(On-line Secret Sharing)

具有除名功能的秘密共享(Secret Sharing with Disenrollment)

实现

1. Shamir的Lagrange插值方法(常用)
2. Blakley的基于矢量空间的几何方法
3. Asmuth和Bloom的中国剩余定理方法

Shamir的(t,n)门限秘密共享方案

参与用户集$U=U_1,U_2,...U_n$，授权集成员数最小为 t，庄家Sam要分享的秘密信息为 s
秘密分享：Sam在$Z_n$上随机选一个次数为$t-1$的秘密多项式$f(x){\in }_R{Z}_n[X]$：$$f(x)=a_0+a_{1}x+...+a_{t-1}{x}^{t+1}modn$$，并满足$f(0)=a_0=s$，同时为U的每个成员选择一个代表其身份的整数$x_i$，Sam计算$s_i=f(x_i)(i=1,2,...,n)$作为子秘密交给$U_i(i=1,...,n)$秘密持有。

信息恢复：随机选取U中的t个成员可以恢复秘密信息s，记这t个成员为$A={U_i}_{j\in \Phi }$，其中$|A|=t$，$\Phi \in 1,2,...,n$，由A中成员所提供的值$(x_i,s_i{)}_{i\in \Phi }$可以恢复s，由Lagrange插值原理（直观理解Lagrange插值法）可得$$f(x)=\sum _{i\in \Phi }{\pi }_i(x)f(x_i)=\sum _{i\in \Phi }{\pi }_i(x)s_i$$，其中 ${\pi }_i(x)={\prod }_{j\in \Phi ,j̸=i}\frac{x-x_i}{x_i-x_j}modn$为Lagrange系数，这样就可以恢复秘密信息$s=f(0)$。

问题：欺诈问题（包括成员欺诈和庄家欺诈），动态增加或删除参与者，对泄露的子秘密的处理和子秘密动态更新问题等。

3. 安全多方计算

内容

安全多方计算(SMC, Secure Multi-party Computation)用于解决一组互不信任的参与方之间保护隐私的协同计算问题，要求n个参与者$(P_1,P_2,...,P_n)$，每个$P_i(i=1,2,...,n)$持有一个秘密输入$x_i$，希望共同计算一个函数$f(x_1,x_2,...,x_n)$，计算结束后要求每方都能得到各自正确的输出，并且自己的秘密输入也没有泄露给其他的参与者。

分类

1. 根据参与方个数的不同，分为2PC和多于3个参与方的MPC。

   安全两方计算所使用的协议为加密电路(Garbled Circuit, GC)+不经意传输(Oblivious Transfer, OT)，安全多方计算所使用的协议为同态加密+秘密分享+OT（+承诺方案+零知识证明等）

2. 根据模型不同，分为半诚实敌手模型和恶意敌手模型。

执行过程

1. 先对输入数据做预处理

   原则：尽量少的数据输入和多的数据预处理

2. 计算逻辑转化为布尔电路

   原则：尽量简单的计算逻辑

   方式：手动/电路编译器Frutta（使用类C的Frutta语言，在JUGO-IDE中编写计算逻辑，通过编译器直接将计算逻辑转换成电路。图灵完备，适配IDE，门槛低。）

3. 将输入的布尔电路做GC和OT算法
   

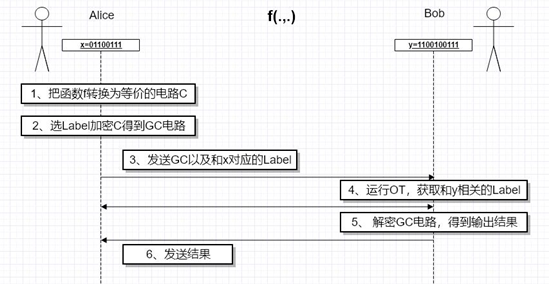
详细算法介绍

1. GC：一种加密计算方式，只揭露计算结果，不揭露输入和中间值，他对电路中的每个运算(AND,OR,NOT)进行加密处理。

   GC过程：

   • 加密：发送方选择label，将电路C进行加密，转换为加密电路C‘；
   • 编码：将电路的输入参数x，通过加密电路的秘密随机值来将x加密为x’；
   • 计算：使用加密电路C’，加密输入参数x‘进行计算，得到电路的输出C(x)

   这里C’和x‘只能计算出C(x)，不会泄露任何x相关的信息。

2. OT：JUGO技术产品使用的是2选1的OT协议，在2选1的OT协议中，发送方有两个消息$m_0$和$m_1$，他要将其中一消息发送给接收方。接收方收到其中一消息后，发送方却不知道发送的是哪一个消息，并且接收方也无法获知另一个消息。OT协议需要消耗大量的信息交互和部分耗时的密码学计算。

   OT协议过程：

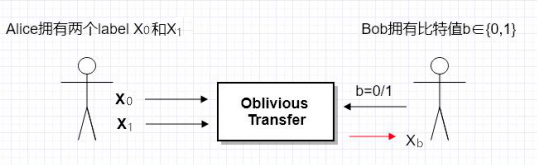
在这个过程中：

• Alice无法获知Bob选择的是哪一个，即Alice不知道b的值；
• Bob无法获知另一个值，即Bob不知道$X_{1-b}$

实战：JUGO

矩阵云推出JUGO安全多方计算平台，针对企业级用户，基于MPC的安全数据交易平台。通过在本地部署MPC节点，进行数据协同计算。

JUGO特性：

• 支持semi-honest通用两方算法：GC+OT。
• 支持Frutta编写的IDE，提供MPC算法的SDK，用户使用IDE和SDK进行开发。
• 支持加法（addition），比较（comparison）多方算法。
• 后续支持通用多方算法和硬件加速

参考：https://jugo.juzix.net/apiDocument

最后

以上就是奋斗鞋子为你收集整理的双线性对的研究以及在分布式系统中的应用的全部内容，希望文章能够帮你解决双线性对的研究以及在分布式系统中的应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。