双线性插值法和nn.functional.conv_transpose2d()

1、nn.ConvTranspose2d和nn.functional.conv_transpose2d的区别

2、双线性插值法原理

3、使用nn.functional.conv_transpose2d()进行双线性插值

1、nn.ConvTranspose2d和nn.functional.conv_transpose2d的区别

1.1 nn.ConvTranspose2d()——

torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0, output_padding=0, groups=1, bias=True, dilation=1, padding_mode=‘zeros’)

• • in_channels (int) – 输入图像的通道数 • out_channels (int) – 由卷积产生的通道数
  • kernel_size (int or tuple) – 卷积核的大小
  • stride (int or tuple, optional) – 卷积的步长. Default: 1
  • padding (int or tuple, optional) – dilation * (kernel_size - 1) - padding 零填充将被添加到输入的每个维度的两边. Default: 0
  • output_padding (int or tuple, optional) – 在输出形状中，添加到每个尺寸一侧的额外尺寸.Default: 0
  • groups (int, optional) – 从输入通道到输出通道的阻塞连接数. Default: 1
  • bias (bool, optional) – If True, adds a learnable bias to the output. Default: True
  • dilation (int or tuple, optional) – 核元素间距. Default: 1
  
  Hout=(Hin−1)×stride[0]−2×padding[0]+dilation[0]×(kernel_size[0]−1)+output_padding[0]+1
  Wout=(Win−1)×stride[1]−2×padding[1]+dilation[1]×(kernel_size[1]−1)+output_padding[1]+1

其对象有两个变量：weight和bias

1.2 torch.nn.functional.conv_transpose2d()

torch.nn.functional.conv_transpose2d(input, weight, bias=None, stride=1, padding=0, output_padding=0, groups=1, dilation=1)→ Tensor
对由多个输入平面组成的输入图像应用二维转置卷积算子。

• input – 输入tensor的形状

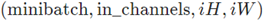
• weight –filters of shape

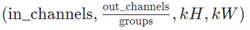
• bias – optional bias of shape (out_channels) . Default: None
• stride – 卷积核的步长. Can be a single number or a tuple (sH, sW). Default: 1
• padding – dilation * (kernel_size - 1) - padding零填充将被添加到输入的每个维度的两边. Can be a single number or a tuple (padH, padW). Default: 0
• output_padding – 在输出形状中，添加到每个尺寸一侧的额外尺寸. Can be a single number or a tuple (out_padH, out_padW). Default: 0
• groups – split input into groups, in_channels 应该设置能被组数整除. Default: 1
• dilation – 核元素之间的间距.Can be a single number or a tuple (dH, dW). Default: 1

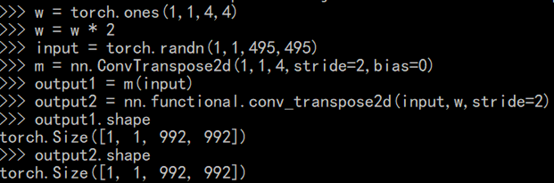
可以看出，输出的shape是相同的

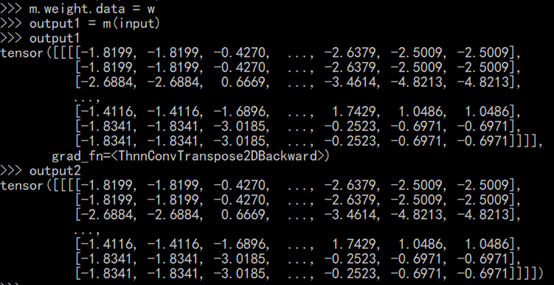
可以看出，连最后结果都是一样的

2、双线性插值法原理

想象一下要把一张低分辨率额图像变成一张高分辨率的图像

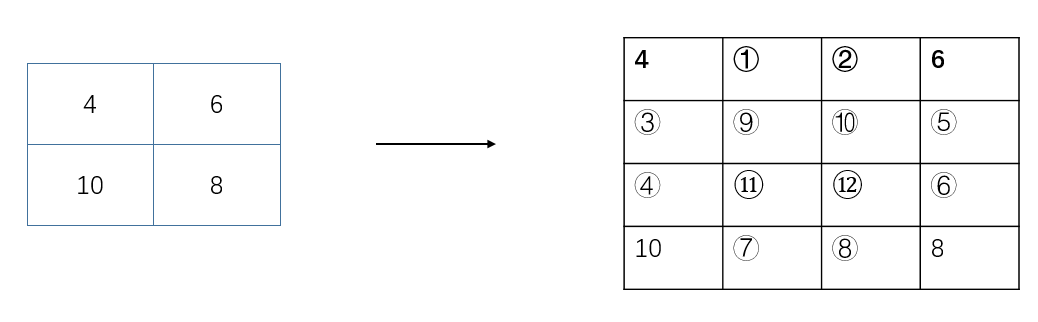
中间的像素点怎么确定呢？就需要用到插值法了

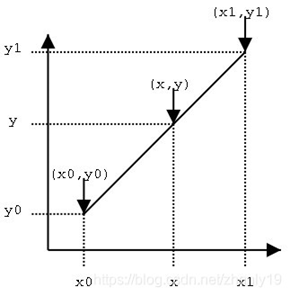
已知点(x0,y0)、(x1,y1)，试问在x处插值，y的值是多少？
根据线性插值公式可以得到：

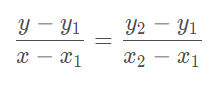
变换一下——








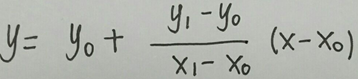
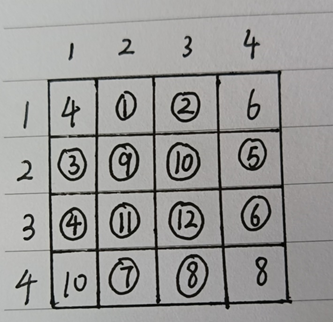
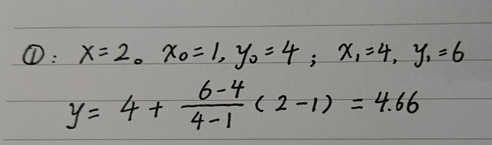
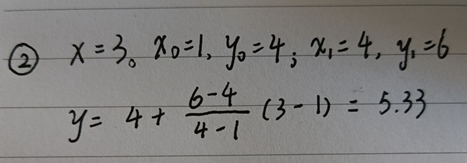
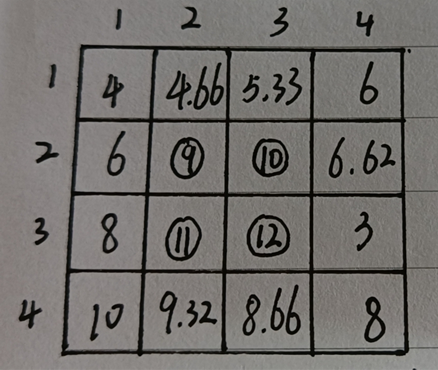
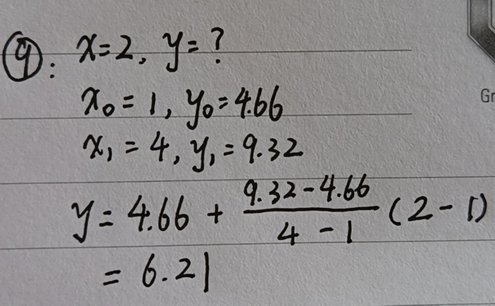
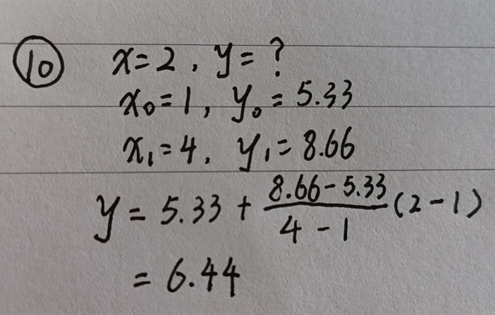
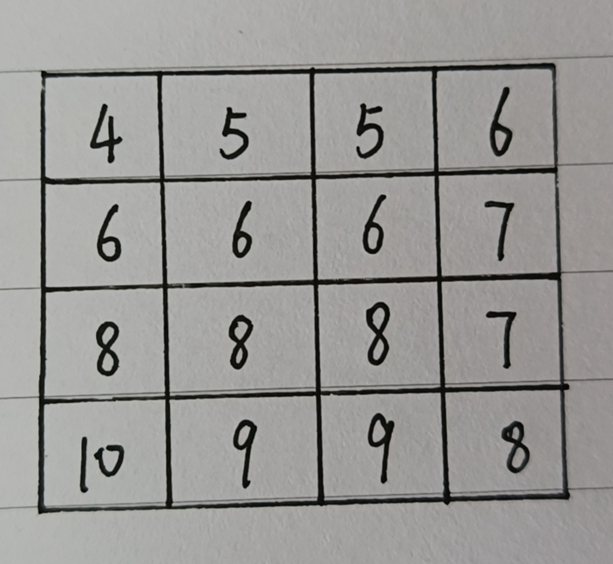
最终结果如下——

扩展到双线性插值法——

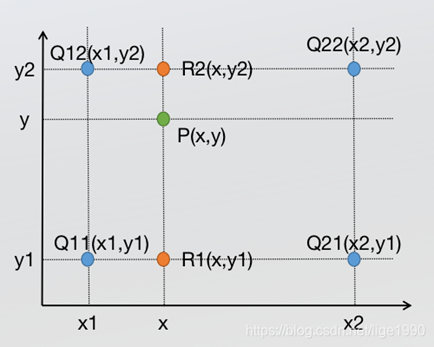
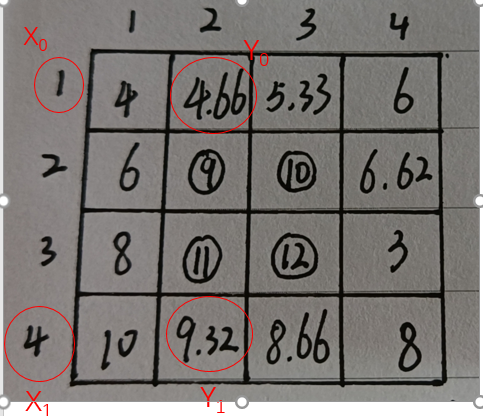
已知Q12，Q22，Q11，Q21，但是要插值的点为P点，这就要用双线性插值了，首先在x轴方向上，对R1和R2两个点进行插值，然后根据R1和R2对P点进行插值，这就是所谓的双线性插值。（实际上调换2次轴的方向先y后x也是一样的结果）

1、x方向单线性插值直接代入前一步单线性插值最后的公式：

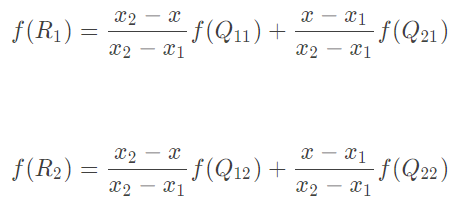
2、y方向单线性插值

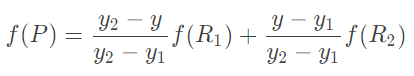
综合起来就是双线性插值最后的结果：

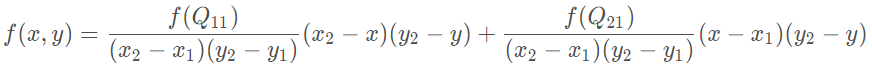
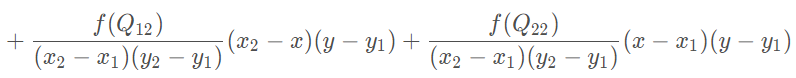
回顾一下上面双线性插值对应关系的图，不难发现，在计算中有这样的关系x2= x1+ 1;y2 = y1 + 1那么上面的公式中的分母全都为1

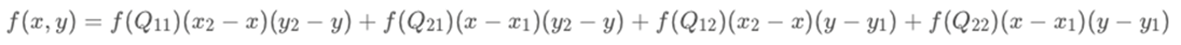
如四个已知点坐标分别为 (0, 0)、(0, 1)、(1, 0) 和 (1, 1)，那么插值公式就可以化简为：

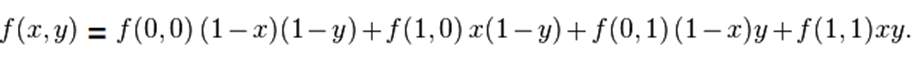
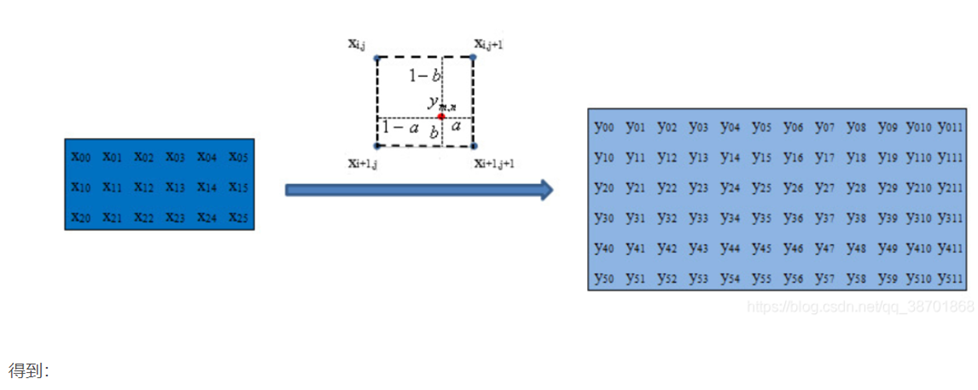
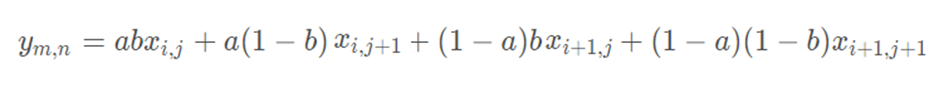
最后就是左边的原始图像经过插值后变成右边的高分辨率的图像了。

3、使用nn.functional.conv_transpose2d()进行双线性插值

nn.functional.conv_transpose2d(input,w,stride=2)这个究竟做了些什么呢？

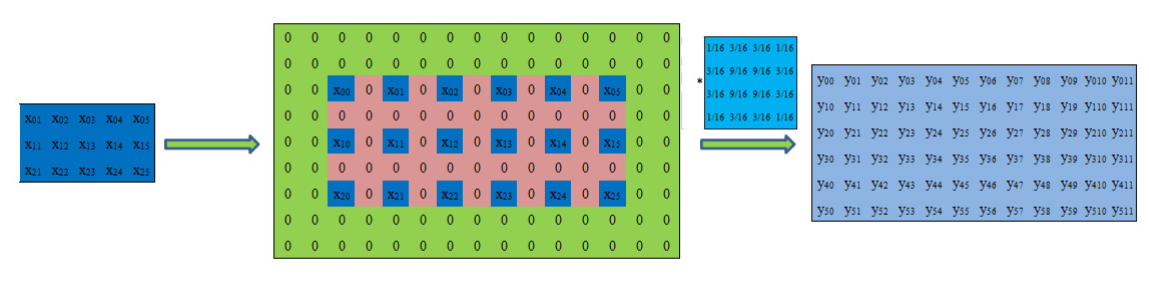
其实反卷积就是将低分辨率的图像通过0填充成很大的图像再卷积成高分辨率的图像。
那么用于插值的权重矩阵怎么来的呢？

def make_bilinear_weights(size, num_channels):
    """ Generate bi-linear interpolation weights as up-sampling filters (following FCN paper). """
    factor = (size + 1) // 2
    if size % 2 == 1:
        center = factor - 1
    else:
        center = factor - 0.5
    og = np.ogrid[:size, :size]
    filt = (1 - abs(og[0] - center) / factor) * (1 - abs(og[1] - center) / factor)
    filt = torch.from_numpy(filt)
    w = torch.zeros(num_channels, num_channels, size, size)
    w.requires_grad = False  # Set not trainable.
    for i in range(num_channels):
        for j in range(num_channels):
            if i == j:
                w[i, j] = filt
    return w

若size=4，num_channels=1时，把4和1代进去factor=2,size=4,所以采样点center是1.5,然后根据这个图求出
1-a=1.5/2=0.75,a=0.25,1-b=0.75,b=0.25


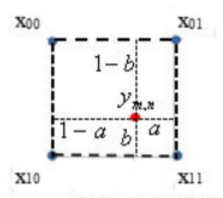
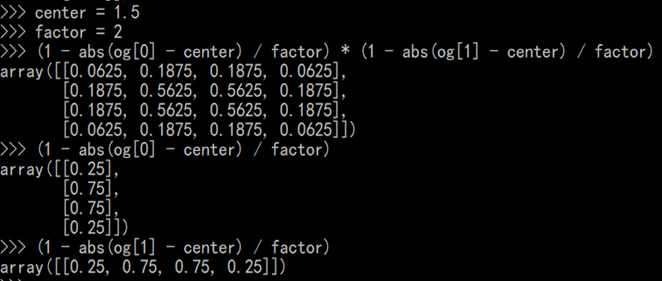
代码中将og[0]作为a，og[1]作为b

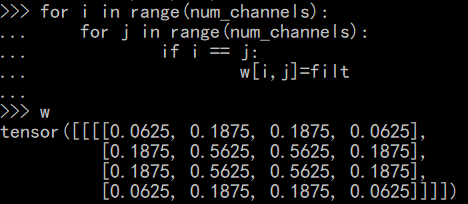
上面得出的权重tensor就是

然后用来与0填充后的矩阵进行卷积操作

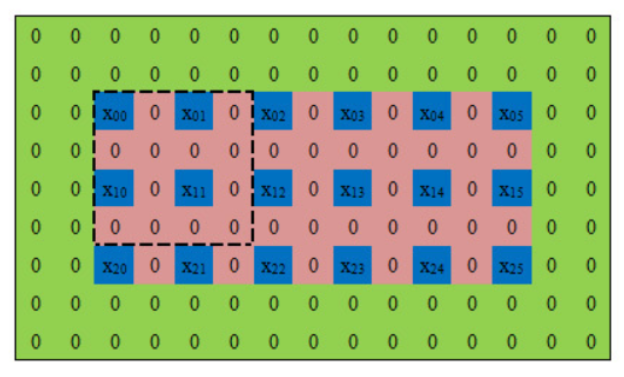
可以发现，跟上面的公式一样——

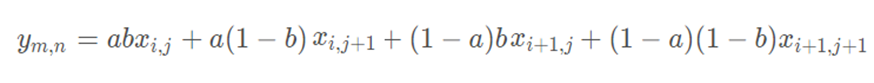
reference

• https://github.com/xwjabc/hed/blob/master/networks.py
• https://pytorch.org/docs/master/generated/torch.nn.ConvTranspose2d.html#torch.nn.ConvTranspose2d
• https://blog.csdn.net/qq_38701868/article/details/103511663
• https://blog.csdn.net/lige1990/article/details/104517342
• https://blog.csdn.net/zhanly19/article/details/99718242/

最后

以上就是俭朴小笼包为你收集整理的双线性插值法和nn.functional.conv_transpose2d()1、nn.ConvTranspose2d和nn.functional.conv_transpose2d的区别2、双线性插值法原理3、使用nn.functional.conv_transpose2d()进行双线性插值的全部内容，希望文章能够帮你解决双线性插值法和nn.functional.conv_transpose2d()1、nn.ConvTranspose2d和nn.functional.conv_transpose2d的区别2、双线性插值法原理3、使用nn.functional.conv_transpose2d()进行双线性插值所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。