我是靠谱客的博主 曾经玉米,这篇文章主要介绍C++(数据结构与算法):61---动态规划、动态规划应用(0/1背包、矩阵乘法链、所有顶点对之间的最短路径、带有负值的单源最短路径、网组的无交叉子集)一、动态规划的思想二、实际应用之最短路径三、实际应用之0/1背包问题四、实际应用之航费五、动态规划递归方程六、编码案例(0/1背包)七、编码案例(矩阵乘法链)八、编码案例(所有顶点对之间的最短路径)九、编码案例(带有负值的单源最短路径)十、编码案例(网组的无交叉子集),现在分享给大家,希望可以做个参考。
一、动态规划的思想
- 动态规划的基础是最优原理
- 动态规划和贪婪算法一样,对一个问题的解是一系列抉择的结果:
- 在贪婪算法中,我们依据贪婪准则做出的每一个抉择都是不可撤销的
- 在动态规划中,我们要考察一系列抉择,以确定一个最优抉择序列是否包含最优抉择子序列
二、实际应用之最短路径
问题描述
- 我们要选择一条从源点s=1到目的顶点d=5的最短路径
动态规划的解决思想
- 第一步:可以选择顶点2、3、4
- 第二步:假设我们选择了顶点3,然后我们要决定从顶点3移动到顶点5
- 第三步:如果我们选择了一条从顶点3到顶点5的路径,但不是最短的。例如选择的子路径为3、2、5,其长度为9,则连起来的路径为1、3、2、5,其长度为11
- 第四步:如果用最短子路径3、4、5代替3、2、5,那么路径1、3、4、5的长度为7
- 因此,在上面我们需要不断的退回与重新判断,寻找到一条从1到5的最短路径,如果不是最短的就重新更换
三、实际应用之0/1背包问题
问题描述
- 有n个物品和一个容量为c的背包。物品i的重量为Wi,价值为p。现在要从n个物品中选出一些物品装入书包中
- 现在的最佳要求是:在装包的物品总重量不超过背包的容量下,使装入的物品总价值最高
- 问题描述是:
- 约束条件是:
- Xi=1表示物品装入背包,Xi=0表示物品没有装入背包
例如
- 假设n=3,w=[100,14,10],p=[20,18,15],c=116
- 如果选择x1=1,则剩余容量为116-100=16,那么接下来可行的解有:
- 如果下一个可行解为[x2,x3]=[1,0],则此次的总价值为100+18=118
- 如果下一个可行解为[x2,x3]=[0,1],则价值为100+15=115。因此,[x2,x3]=[0,1]并非最优解,所以要退回到第一步,选择x=[1,1,0]这个序列
- 如果选择x1=0,则剩余容量为116,那么接下来可行的解有:
- 如果下一个可行解为[x2,x3]=[1,1],则此次的总价值为18+15=33。因此,[x2,x3]=[1,1]并非最优解,那么需要退回到最开始,重新选择x1=1,然后再继续进行动态规则
四、实际应用之航费
问题描述
- 某航线价格表为:
- 票价为$100的航线:从亚特兰大到纽约/或芝加哥;或从洛杉矶到亚特兰大
- 票价为$20的航线:从芝加哥到纽约;或对于途径亚特兰大的旅客,从亚特兰大到芝加哥
- 为了省钱,需要选择中转机场:
- 如果用(起点,终点)表示问题状态,那么在选择从洛杉矶到亚特兰大后,问题状态变成(亚特兰大,纽约)
- 从亚特兰大直达纽约的票价为$100,所以从洛杉矶到纽约机票为$200
- 让从亚特兰大途径芝加哥再到纽约的票价为$40.因此洛杉矶——亚特兰大——纽约的总票价为$140
- 如果使用三元组(tag,起点,终点)表示问题状态,其中tag为0表示转飞,tag为1表示其他情形,那么在到达亚特兰大后,问题状态变为(0,亚特兰大,纽约),它的最优路径是以芝加哥为中转机场
五、动态规划递归方程
- 当最优抉择包含最优子序列时,可建立动态规划递归方程,它可以帮助我们高效地解决问题
0/1背包问题案例
- 在文章上面提到的背包问题中,最优选择序列由最优选择子序列构成
- 假设f(i,y)表示剩余容量为y,剩余物品为i,i+1,...,n的背包问题的最优解的值,即:
- 无论第一次的选择是什么,接下来的选择一定是当前状态下的最右选择,我们称此为“最优原则”。它意味着一个最优选择序列是由最优选择子序列构成的。但是,最优原则可能对某些问题的求解并不适用,这时就不能应用动态规划
- 应用动态规划求解的步骤如下:
- 1)证实最优原则是适用的
- 2)建立动态规划的递归方程式
- 3)求解动态规划的递归方程式以获得最优解
- 4)沿着最优解的生成过程进行回溯
- 编写一个简单的递归方程来求解动态规划方程是一件很诱人的事。然而,我们将在后面的动态规划应用文章中看到,如果不能避免重复计算,递归方程的复杂度将非常可观。如果避免了重复计算,复杂度将急剧下降。动态规划递归方程也可用迭代方法来求解,这时就自然避免了重复计算。其实,迭代程序与避免了重复计算的递归程序有相同的复杂度,但是迭代程序不需要附加的递归栈空间,因此将比后者运行更快
六、编码案例(0/1背包)
- 待续
七、编码案例(矩阵乘法链)
- 待续
八、编码案例(所有顶点对之间的最短路径)
- 待续
九、编码案例(带有负值的单源最短路径)
- 待续
十、编码案例(网组的无交叉子集)
- 待续
最后
以上就是曾经玉米最近收集整理的关于C++(数据结构与算法):61---动态规划、动态规划应用(0/1背包、矩阵乘法链、所有顶点对之间的最短路径、带有负值的单源最短路径、网组的无交叉子集)一、动态规划的思想二、实际应用之最短路径三、实际应用之0/1背包问题四、实际应用之航费五、动态规划递归方程六、编码案例(0/1背包)七、编码案例(矩阵乘法链)八、编码案例(所有顶点对之间的最短路径)九、编码案例(带有负值的单源最短路径)十、编码案例(网组的无交叉子集)的全部内容,更多相关C++(数据结构与算法):61---动态规划、动态规划应用(0/1背包、矩阵乘法链、所有顶点对之间内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。

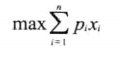










发表评论 取消回复