00摘要

环岛元素是智能车比赛中较难处理的元素之一。比赛要求智能车能检测到环岛并从入口驶入,在绕行约 270°后驶出环岛,其中,能否高响应、高鲁棒性地检测环岛是后续进出环岛等步骤的基础。本文根据计算机视觉中的多视图几何学证明了环岛椭圆投影的存在,使用优化的最小二乘法拟合法并结合相关限制条件以识别环岛。
▲ 主板PCB
01引言

环岛元素是智能车比赛中较难处理的元素之一,由于车身在行驶过程中存在不确定性,故难以保证稳定识别效果。如图 1-1 与图 1-2 所示。

▲ 图 C-1 环岛灰度图

▲ 图 C-2 环岛二值化图
本文分析了传统电磁识别与摄像头识别环岛的优点和缺点,首先证明了环岛椭圆投影的正确性,然后此基础上提出了一种基于椭圆拟合的环岛识别方法,通过拉格朗日算子优化最小二乘误差函数使其最小化,并将结果转化为特征向量的形式。最后通过仿真和实验验证了此环岛识别方案的性能,并给出方案评价与可进一步研究的方向。
02现状和方法

从信息获取的不同方式上来说,环岛检测方案可以分为摄像头识别和电磁识别。
2.1 电磁识别
智能车大赛道路中先布置了通有 20kHz、100mA 交变电流的中心电磁引导线,频率范围 20k±1kHz,电流范围 100±20mA。由于电磁引导线完全绕行与环岛,在环岛圆与赛道的交点处可等效为两倍电磁场,故可在智能车前支架配置
电感检测装置以检测智能车是否到达环岛入口处,即点 B 处。若电磁测量值约为正常行驶时的两倍,可置入环标志位。
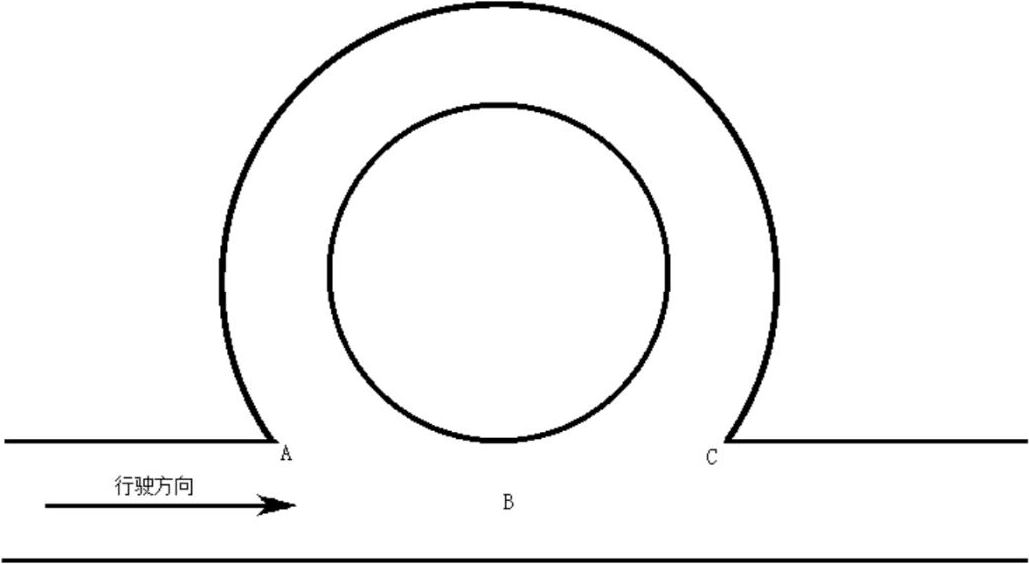
▲ 图 C-3 环岛示意图
此方案的缺点在于滞后检测效应。当通过摄像头正常寻迹时,由于车身到入环点才能检测到环岛,车辆在 A、B 点之间时,由于左侧赛道缺失,智能车会往左侧偏移,随后因扫描到环岛内沿而校正回来,该过程使智能车震荡,导致行驶
到 B 点处位置可能发生偏移,导致电感检测失败。此外,对于摄像头为主要寻迹传感器的智能车,多加电磁传感器使系统更加冗余复杂。
2.2 摄像头识别
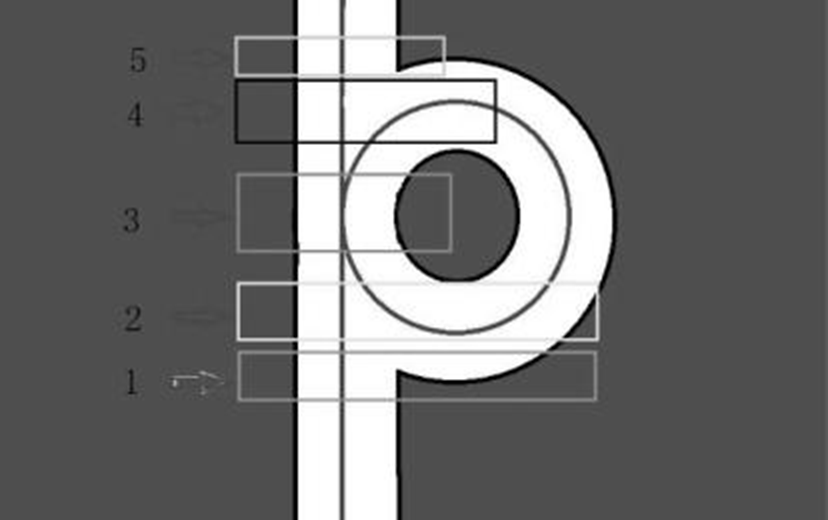
▲ 图 C-4 流程式环岛识别
一种常规的,利用摄像头进行环岛入口识别的方法如下。
(1) 右侧赛道突然变宽,左侧赛道正常,标志位置为 1。
(2) 右侧赛道丢线,左侧赛道正常,标志位置为 2。
(3) 右侧赛道由宽变窄,随后又逐渐变宽,左侧赛道不变,标志位置为 3。
(4) 右侧赛道再次丢线,标志位置为 4。
(5) 若标志位等于 4,则识别到环岛。
该方案计算量较小,但仍然存在滞后检测效应,智能车会在区间 2 处小幅度右转,影响后续过程的判断过程。除此之外,该方案为流程化方案,若在判断过程中有一个步骤意外出错都无法正确判断为环岛入口,导致智能车无法入环甚至冲出赛道。
03环岛椭圆投影

对椭圆的投影进行建模,如下图所示。将P平明的圆投影到H平面。设P平面的椭圆长半轴长度为A,短半轴的长度为B。P平面与H平面的夹角为
α
alpha
α。
取 0 0 < α < 9 0 0 0^0 < alpha < 90^0 00<α<900。于P平面建立笛卡尔坐标系XOY,椭圆长轴在X轴上,椭圆短轴在Y轴上,线段OO1的长度为L。可以平面P上的椭圆方程为:
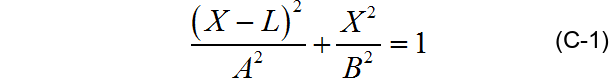
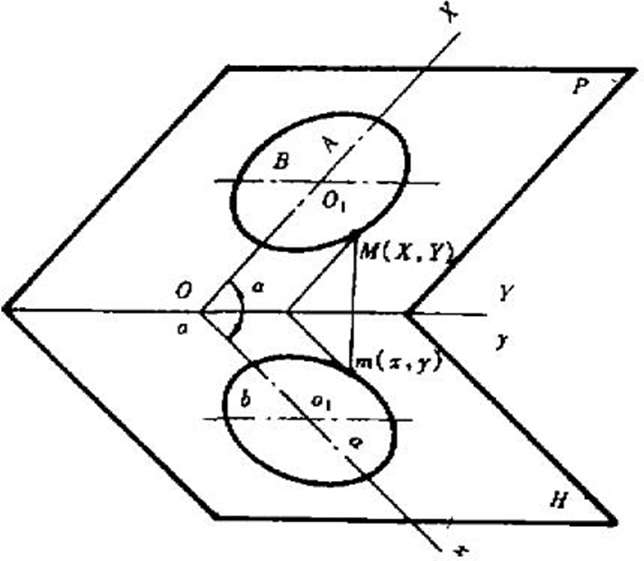
▲ 图 C-5 椭圆映射图
一束平行光以 O 1 o 1 O_1 o_1 O1o1的方向照烧,是P平面椭圆映射在H平面上,形成椭圆o1。
在平面H上建立笛卡尔坐标系,oy与OY相重合,OX投影于ox,椭圆上一点M(X,Y)投影到m(x,y),可知两平面的坐标系关系为:
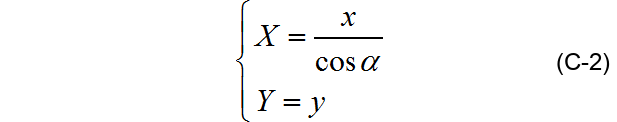
联立C-1与C-2,得:
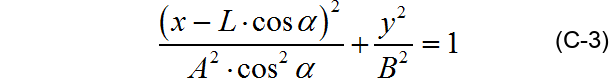
令
m
=
A
⋅
cos
α
,
n
=
B
,
p
=
L
⋅
cos
α
m = A cdot cos alpha ,,,n = B,,,p = L cdot cos alpha
m=A⋅cosα,n=B,p=L⋅cosα
将C-3记作:
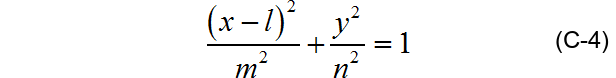
显然,C-4为椭圆方程,即平面P上的椭圆经过平行光投影后仍然是椭圆。
特殊的,当平面P上的椭圆为圆时,有:
L
=
0
,
A
=
B
=
R
L = 0,A = B = R
L=0,A=B=R,则C-3为:
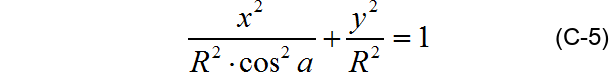
令
m
′
=
R
⋅
cos
α
,
n
′
=
n
m' = R cdot cos alpha ,,,n' = n
m′=R⋅cosα,n′=n,平面H上的投影为:
x
2
m
′
2
+
y
2
n
′
2
=
1
{{x^2 } over {m'^2 }} + {{y^2 } over {n'^2 }} = 1
m′2x2+n′2y2=1
显然,当 cos α ≠ 1 cos alpha ne 1 cosα=1时, m ′ ≠ n ′ m' ne n' m′=n′,该解析式描述的为椭圆。
对于环岛元素,设内环岛边缘为平面P上的圆。自然光线在P平面上的发生反射。由于物象距离较远,反射光可近似为平行光。根据摄像机的真空成像模型,反射光在详平面成像,即图像平面为H平面。因此,只需验证内环岛边缘微椭圆即可。
▲ C 车模电机驱动PCB
04最小二乘拟合

设椭圆一般方程为:
F
(
a
,
x
)
=
a
⋅
x
=
a
x
2
+
b
x
y
+
c
y
2
+
d
x
+
e
y
+
f
=
0
Fleft( {a,x} right) = a cdot x = ax^2 + bxy + cy^2 + dx + ey + f = 0
F(a,x)=a⋅x=ax2+bxy+cy2+dx+ey+f=0
其中,
a
=
[
a
,
b
,
c
,
d
,
e
,
f
]
T
a = left[ {a,b,c,d,e,f} right]^T
a=[a,b,c,d,e,f]T
x = [ x 2 , x y , y 2 , x , y , 1 ] T x = left[ {x^2 ,xy,y^2 ,x,y,1} right]^T x=[x2,xy,y2,x,y,1]T
对于一个待拟合的离散点集合, X i = ( x , y ) X_i = left( {x,y} right) Xi=(x,y), F ( a , X i ) Fleft( {a,X_i } right) F(a,Xi)表示点Xi到椭圆 F ( a , x ) Fleft( {a,x} right) F(a,x)的几何距离。
最小二乘法的目标是求取使得李散掉的几何距离最短的a,即最小化:
D
a
=
∑
i
=
1
N
F
(
a
,
X
i
)
2
D_a = sumlimits_{i = 1}^N {Fleft( {a,X_i } right)^2 }
Da=i=1∑NF(a,Xi)2
由于环岛内边缘投影为椭圆,而F(a,x)为广义圆锥曲线一般表达式,需要表示为添加约束条件,以保证你和结果仅为椭圆。即:
4
a
c
−
b
2
=
1
4ac - b^2 = 1
4ac−b2=1
为了表达方便,将前面方程吧粗歘在:
a T C a = 1 a^T Ca = 1 aTCa=1
其中:
c
=
[
0
0
2
0
0
0
0
−
1
0
0
0
0
2
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
]
c = begin{bmatrix} begin{matrix} 0 & 0 & 2 & 0 & 0 & 0\0 & { - 1} & 0 & 0 & 0 & 0\2 & 0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0 & 0\0 & 0 & 0 & 0 & 0 & 0\end{matrix} end{bmatrix}
c=⎣⎢⎢⎢⎢⎡002000−100020000000000000000000⎦⎥⎥⎥⎥⎤
故问题转换为最小化误差函数:
E
=
∥
D
a
∥
2
E = left| {Da} right|^2
E=∥Da∥2
约束条件为: a T C a = 1 a^T Ca = 1 aTCa=1
其中矩阵: D = [ X 1 X 2 ⋯ X N ] D = left[ {X_1 X_2 cdots X_N } right] D=[X1X2⋯XN]
对于一个离散点:
X
i
=
[
x
2
,
x
y
,
y
2
,
x
,
y
,
1
]
X_i = left[ {x^2 ,xy,y^2 ,x,y,1} right]
Xi=[x2,xy,y2,x,y,1]
根据拉格朗日乘子法,求解
z
=
f
(
x
,
y
)
z = fleft( {x,y} right)
z=f(x,y)在条件
ϕ
(
x
,
y
)
=
1
phi left( {x,y} right) = 1
ϕ(x,y)=1下的极值,构造Lagrange函数:
L
(
x
,
y
,
λ
)
=
f
(
x
,
y
)
+
λ
ϕ
(
x
,
y
)
Lleft( {x,y,lambda } right) = fleft( {x,y} right) + lambda phi left( {x,y} right)
L(x,y,λ)=f(x,y)+λϕ(x,y)
令:
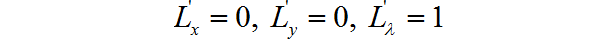
求出x,y,lambda,可以得到:
2
D
T
D
a
−
2
λ
C
a
=
0
2D^T Da - 2lambda Ca = 0
2DTDa−2λCa=0
令
D
T
D
=
S
D^T D = S
DTD=S,则有:
S
a
=
λ
C
a
Sa = lambda Ca
Sa=λCa
由于S为实对称矩阵,C为正定矩阵,故求解是为求解广义特征值问题。C正定,用
C
−
1
C^{ - 1}
C−1做成上式,可以得到:
C
−
1
S
a
=
λ
a
C^{ - 1} Sa = lambda a
C−1Sa=λa
令
p
=
C
−
1
S
p = C^{ - 1} S
p=C−1S则:
p
a
=
λ
a
pa = lambda a
pa=λa
所以只需要求解上式的特征向量a即可。根据数值分析幂法可求。
05限制条件

根据椭圆一般方程:
F ( a , x ) = a ⋅ x = a x 2 + b x y + c y 2 + d x + e y + f = 0 Fleft( {a,x} right) = a cdot x = ax^2 + bxy + cy^2 + dx + ey + f = 0 F(a,x)=a⋅x=ax2+bxy+cy2+dx+ey+f=0
可的长半轴长度平方:
A
2
=
2
(
a
X
c
2
+
c
Y
c
2
+
b
X
c
Y
c
−
1
)
a
+
c
+
(
a
−
b
)
2
+
b
2
A^2 = {{2left( {aX_c^2 + cY_c^2 + bX_c Y_c - 1} right)} over {a + c + sqrt {left( {a - b} right)^2 + b^2 } }}
A2=a+c+(a−b)2+b22(aXc2+cYc2+bXcYc−1)
其中椭圆几何中心:
X
c
=
b
e
−
2
c
d
4
a
c
−
b
2
,
Y
c
=
b
d
−
2
a
e
4
a
c
−
b
2
X_c = {{be - 2cd} over {4ac - b^2 }},,,,Y_c = {{bd - 2ae} over {4ac - b^2 }}
Xc=4ac−b2be−2cd,Yc=4ac−b2bd−2ae
根据世纪环岛的映射特点,限定如下识别条件:
(1)环岛映射非长扁椭圆,约束为
0.2
<
A
B
<
5
0.2 < {A over B} < 5
0.2<BA<5。
(2)椭圆几何中心在左上侧,或者右上侧,约束为
Y
C
>
H
2
Y_C > {H over 2}
YC>2H,H为图像高度;
(3)以右环岛为例,为保证提前识别,约束为右下侧出现环岛尖角。
06实验结果

以图C-2为计算示例,取内环岛边缘点获取坐标。

使用MATLAB 仿真得到椭圆方程为:
F ( a , x ) = 0.00154 x 2 − 0.019 x ⋅ y − 0.156 x Fleft( {a,x} right) = 0.00154x^2 - 0.019x cdot y - 0.156x F(a,x)=0.00154x2−0.019x⋅y−0.156x + 0.195 ⋅ y 2 − 3.390 y + 38.870 + 0.195 cdot y^2 - 3.390y + 38.870 +0.195⋅y2−3.390y+38.870
椭圆参数为:
A
=
30.537
,
B
=
5.099
,
X
c
=
150.053
,
Y
c
=
15.788
A = 30.537,,,B = 5.099,,,,X_c = 150.053,,,Y_c = 15.788
A=30.537,B=5.099,Xc=150.053,Yc=15.788
07总结和展望

本文提出了一种基于椭圆拟合的环岛识别方法,相比于传统的摄像头识别与电感识别方法,该方法有以下特点。
(1) 无需流程式判断,降低整体误判断概率。
(2) 具有远前瞻特性,以免智能车因丢线而误转向。
(3) 利用最小二乘的结果代替了程序迭代过程,提高了运算速度。
通过实验分析研究表明,本文的方案有较快的运算速度、较强的棒性,不过仍有许多需要改进的地方,可在本文的基础上进行以下深入研究。
(1) 寻找更好的求解特征向量方法,进一步加快整体运算速度。
(2) 由于摄像机像素较小,对于较小的椭圆难以正确拟合与判断,可使用更高素质的摄像机。
(3) 由于车身位置变化,导致稳定寻找内环岛边缘区位置有一定困难,需要寻找更好的搜索方法。
▲ 车模电机驱动PCB
08参考文献

[1] 彭慧敏. 平面斜截正圆锥截交线为椭圆时投影曲线分析. 西安建筑科技大学学报: 自然科学版, 1998. 30(2): 第189-191页.
[2] 莫章金. 椭圆的投影及其应用. 重庆建筑高等专科学校学报, 1999. 9(2): 第28-31页.
[3] Fitzgibbon, A., M. Pilu and R.B. Fisher, Direct least square fitting of ellipses. IEEE Transactions on pattern analysis and machine intelligence, 1999. 21(5): p. 476-480.
[4] Hal?r, R. and J. Flusser. Numerically stable direct least squares fitting of ellipses. 1998: Citeseer.
[5] 李成章, 黄玉民. 数学分析. 上北京: 科学出版, 1999.
[6] Trefethen, L.N. and D. Bau III, Numerical linear algebra. Vol. 50. 1997: Siam.
[7] 封建湖. 数值分析原理. 2001: 科学出版社.
最后
以上就是怕孤独皮皮虾最近收集整理的关于基于椭圆拟合的环岛识别方法00摘要01引言02现状和方法03环岛椭圆投影04最小二乘拟合05限制条件06实验结果07总结和展望08参考文献的全部内容,更多相关基于椭圆拟合内容请搜索靠谱客的其他文章。








发表评论 取消回复