文章目录
- 1.基础原理与仿真程序
- 2.QPSK多径信道仿真
- 3.归一化相关
- ps
此博文是对于QPSK信号基本原理和经过多径仿真情况下的仿真,未考虑电路和载波!
1.基础原理与仿真程序
- 原理
正交相移键控(Quadrature Phase Shift Keying,QPSK)是一种数字调制方式。
星座图(constellation diagram)有助于定义信号元素的振幅和相位,尤其当我们使用两个载波(一个同相,而另一个正交)时。当处理多电平ASK,PSK或QAM(见下一个节)时,星座图很有用。
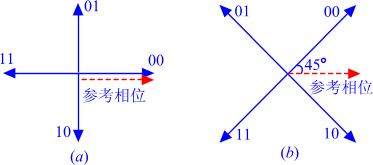
两种常见用QPSK星座图相位
- 程序
a.利用Matlab中调制(pskmod)解调(depskmod)函数实现
M=4;
a=randi([0 1],1,10);
a2= reshape(a,log2(M),[])' %★以每组2比特进行分组,M=4
a10= bi2de(a2) %二进制转化为十进制
yt=pskmod(a10,M,pi/4)
yj=pskdemod(yt,M,pi/4)
De_data1 = reshape(yj,[],1)
De_data2 = de2bi(De_data1,2)
b = reshape(De_data2',1,[])
b.自编原理型实现(+awgn)
输入一组随机初始信息x=[01矩阵];
按两两一组通过for循环判别4种组合,分别对应星座图4个点;
做星座图
调制和解调相对应
%此代码实现QPSK调制与解调,并加噪做误码率曲线
close all;clc;
SNR=1:20; %信噪比变化范围
snr=10.^(SNR/10); %将信噪比转化成直角坐标
N=100000; %仿真点数
M=1;
a=randi([0,1],1,N); %产生一组随机初始信息矩阵
[r,c] = size(a); %读取行r、列c
y=[];
for u=1:r %建立for循环嵌套,寻找4种组合→映射到星座图位置
p=1;
for t=1:2:c
k=t+1;
if a(u,t)==0&&a(u,k)==0
y(u,p)=-1-1i;
elseif a(u,t)==0&&a(u,k)==1
y(u,p)=-1+1i;
elseif a(u,t)==1&&a(u,k)==0
y(u,p)=1-1i;
else
y(u,p)=1+1i;
end
p=p+1;
end %"y1=pskmod(y0,M)"Matlab自带的psk调制函数
end % "scatterplot(y)"可做画星座图 验证
for i=1:length(SNR)
N0=1/2/snr(i); %计算噪声功率
N0_dB=10*log10(N0); %将噪声功率转换为dBW
ni=wgn(1,N/2,N0_dB); %产生高斯噪声
ys=y+ni; %通过高斯信道
[n,m] = size(ys);
q=[]; % BER_S=zeros(1,20);BER_S可预先分配空间,提升性能
for b=1:n % 与调制对应,用for循环QPSK解调(将4个星座点数据输出为01序列)
j=1;
for d=1:m
if real(ys(b,d))<0&&imag(ys(b,d))<0
q(b,j)=0;q(b,j+1)=0;
elseif real(ys(b,d))<0&&imag(ys(b,d))>0
q(b,j)=0;q(b,j+1)=1;
elseif real(ys(b,d))>0&&imag(ys(b,d))<0
q(b,j)=1;q(b,j+1)=0;
elseif real(ys(b,d))>0&&imag(ys(b,d))>0
q(b,j)=1;q(b,j+1)=1;
end
j=j+2;
end
end %"y2=pskdemod(y1,M)"Matlab自带的psk解调函数
[number1,BER_S(i)] = symerr(a,q); %计算错误比特数和误码率(误比特率)== bit_A=length(find(a~=q))%统计错误比特数 p=number1/N;
end
BER_T=1/2*erfc(sqrt(snr/2)); %AWGN信道下QPSK理论误码率
%绘制图形
figure;
semilogy(SNR,BER_S,'-k*');hold on;
semilogy(SNR,BER_T,'-go');hold on;
legend('仿真','理论');
axis([-1,10,10^-4,1]);
title('QPSK误码性能分析');
xlabel('信噪比SNR(dB)');ylabel('BER');
- 运行结果
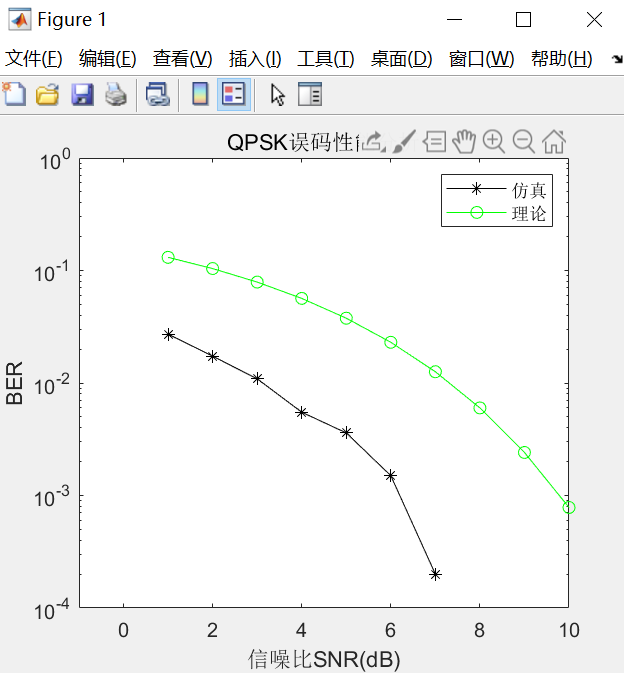
2.QPSK多径信道仿真
多径信道:信号通过多条路径抵达接收端,由散射等引起,是时延。
均衡:校正信道引入的失真,使得信道和均衡器的传输函数的乘积为常数,消除码间串扰。
ZF:Zero forcing迫零均衡,就是忽略噪声,迫使噪声为0。简单,但放大了噪声,性能最差;
MMSE:Minimum Mean Square Error,最小均方误差均衡,让系统最小均衡误差达到最小从而推出均衡矩阵,考虑了噪声因素,性能比ZF好;
MLSE:Maximum Likelihood Sequence Estimation, 最大似然均衡,考虑了有效发送序列与信道冲击响应卷积后可能形成的所有序列,从中找到与接收信号有最小距离的序列,性能优于另外两种,但复杂度最大。
下边程序为QPSK信号通过多径信道,并且做了上述三种均衡来补偿,并做误码率曲线做性能对比
- 程序
close all;clc;
%% 参数设置
SNR=1:20; %信噪比变化范围
snr=10.^(SNR/10); %将信噪比转化成直角坐标
M=4;
N=200;
pathnum=3;
l_cp=pathnum+1;
w1=zeros(2*M,N);
w2=zeros(2*M,N);
w3=zeros(2*M,N);
%生成输入所有可能序列,备MLSE使用
xq=[0.7071 + 0.7071i;-0.7071 - 0.7071i;0.7071 - 0.7071i;-0.7071 + 0.7071i];
b=[0.7071 + 0.7071i,-0.7071 - 0.7071i,0.7071 - 0.7071i,-0.7071 + 0.7071i];
for nmnm=M:-1:2
xq=Tmultiply(xq,b);
end
xq;
length(xq); %4^M次方个组合
%% 初始序列生成qpsk调制
for ii=1:length(SNR)
a=randi([0 1],1,2*M*N);
a2= reshape(a,log2(4),[])';
a10= bi2de(a2);
xt=pskmod(a10,4,pi/4);
x=reshape(xt,M,N); %M×N
x1=zeros(M+l_cp,1);
x2=zeros(M,1);
for jj=1:N
%% 多径信道
h=(randn(1,pathnum)+1i*randn(1,pathnum))*sqrt(1/2/pathnum);%信道设置
x2=x(:,jj);
x1=[x2(M-l_cp+1:M);x2]; %+cp x1=[M+1×1]
y0=conv(x1,h); %y=x*h
y=y0(l_cp+1:l_cp+M,:); %-cp Y=[M×1]
%% awgn
[m,n]=size(y);
N0=1/2/snr(ii);
N0_dB=10*log10(N0);
ni=wgn(m,n,N0_dB);
ys=y+ni;
%% 接收端
% 均衡矩阵
H=zeros(M,M);
H1=zeros(M,1);
for kk=1:pathnum
H1(kk)=h(kk);
end
H(:,1)=H1; %第一列
for cc=1:M-1
H(:,cc+1)=circshift(H1,cc);
end %第一列依次循环移位置2→M-1列
%H·X=Y
H;
% ZF均衡
x_dect1=Hys;
xxx1=reshape(x_dect1,[],1);
yj1=pskdemod(xxx1,4,pi/4);
De_data11 = reshape(yj1,[],1);
De_data21 = de2bi(De_data11,2);
w1(:,jj)= reshape(De_data21',[],1);
% MMSE均衡
[nn1,mm1]=size(H*H');
W=H'*pinv(H*H'+1/SNR(ii)*eye(nn1,mm1));
x_dect2=W*ys;
xxx2=reshape(x_dect2,[],1);
yj2=pskdemod(xxx2,4,pi/4);
De_data12 = reshape(yj2,[],1);
De_data22 = de2bi(De_data12,2);
w2(:,jj)= reshape(De_data22',[],1);
% ML均衡
size(H);
for iii=1:4^M
xg(iii)=norm(ys-H*xq(iii,:).');
end
minxg=min(xg);
for jjj=1:4^M
if xg(jjj)==minxg
aaa=jjj;
end
end
xxx=reshape(xq(aaa,:),[],1);
yj=pskdemod(xxx,4,pi/4);
De_data1 = reshape(yj,[],1);
De_data2 = de2bi(De_data1,2);
w3(:,jj)= reshape(De_data2',[],1);
end
q1=reshape(w1,1,2*M*N);
[number1,BER_S1(ii)] = symerr(a,q1); %计算错误比特数和误码率
q2=reshape(w2,1,2*M*N);
[number1,BER_S2(ii)] = symerr(a,q2); %计算错误比特数和误码率
q3=reshape(w3,1,2*M*N);
[number1,BER_S3(ii)] = symerr(a,q3); %计算错误比特数和误码率
end
BER_S1
BER_S2
BER_S3
%% 绘制图形
figure;
semilogy(SNR,BER_S1,'-b*');hold on;
semilogy(SNR,BER_S2,'-r*');hold on;
semilogy(SNR,BER_S3,'-g*');hold on;
text(10,0.079,'ZF');
text(10,0.038,'MMSE');
text(10,0.01,'ML');
axis([-1,20,10^-4,1]);
title('误码性能分析');
xlabel('信噪比SNR(dB)');ylabel('误码率BER');
- Tmultiply
一个自建子函数,用于实现以下功能:
一个位置上有m种可能,一共n个位置,求所有可能的组合
解法:分解法
把这个过程拆分为2个为一组的多个二元运算。
假设n=3,m=2,那2^3=222=(22)2=42,转换成数组也是一样的
所以可以定义一种特殊的乘法:两个数组中的元素两两组合
假设:m=[1,2]
mmm=(mm)m
mm=[1,2][1,2]=[[1, 1], [1, 2], [2, 1], [2, 2]]
(mm)*m=[[1, 1, 1], [1, 1, 2], [1, 2, 1], [1, 2, 2], [2, 1, 1], [2, 1, 2], [2, 2, 1], [2, 2, 2]]
只需要使用这种特殊的乘法,每次都乘上一个m,n-1次运算后便可得到结果。
function r=Tmultiply(a,b)
r=[]; k=1;
[p,~]=size(a);
[~,nn]=size(b);
for i=1:p
for j=1:nn
r(k,:)=[a(i,:),b(:,j)];
k=k+1;
end
end
- 运行结果
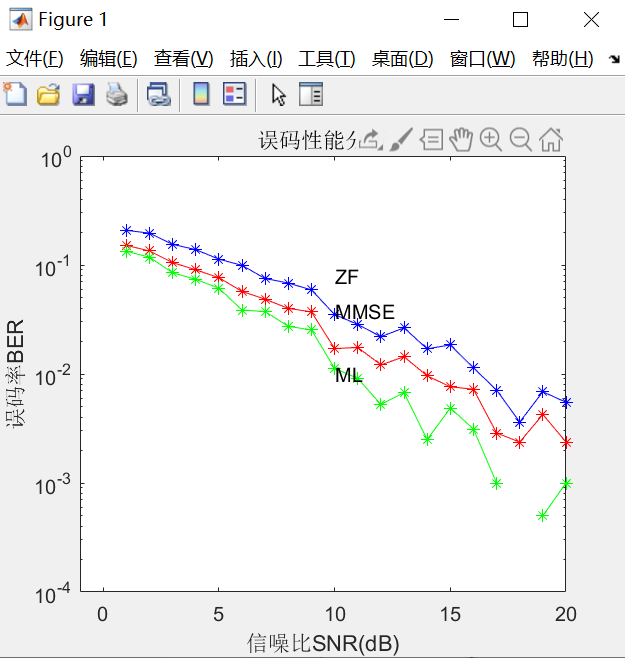
可以看到,性能优劣和最初原理分析时所述一致。
增大序列长度M和序列数N会使曲线更平滑,但由于MLSE均衡复杂度大(需要生成4^M个序列),计算过程也会相对较慢。
3.归一化相关
转于:Here
- 星座映射归一化因子是如何得到的?
答:所有能量求平均后开方得到的就是波形幅度值,其倒数就是归一化因子。比如,
比如16QAM,取值为,能量为2有4个星座点,为10有8个点(±1±3i),为18有4个点,共有能量72+80+8=160,然后这16个点的等概率分布是16分之1,所以要160除以16=10,这是平均能量,其平均后的波形幅度为sqrt(10),而QPSK共4个能量为2的星座,出现概率为四分之一,所以为8除以4=2,结果为sqrt(2),其他类推。
- 能量(功率)归一化有什么用?
答:添加功率归一化因子,目的在于使得不同调制方式(或者说对于所有映射方式)都能够取得相同的平均功率。
实际上,归一化是为了方便系统性能的比较,所以就要分清比较的模块是什么。比如,信道编码的增益问题,无论有无信道编码,比特能量是一样的,所以比较要以Eb/No为基准,而不是以进入信道前的符号能量Es/No为基准。再比如,在比较空时码系统和单天线系统中,还是以进入时空码编码前信号能量为基准,那么发送时的总能量一致,即时空码系统中各天线发射功率总和应和单天线系统发射功率相同。一般而言,归一化都在发射端处理。
- 在仿真OFDM的IFFT变换时,为什么要乘以sqrt (fft的点数) 进行归一化?
答:在matlab中做完IFFT后要乘以sqrt(fft的点数),这样才能保证时域和频域上的功率相同,否则在计算功率上容易出错,如果不乘的话你只要知道也是可以的。至于信号功率归一化,是为了更方便的计算SNR,是为了在相同的标准下比较性能。
ps
Ⅰ.归一化不太会(信号噪声…)
Ⅱ.通信小白,摸索ing
相关博文
1.OFDM基础与多径仿真
2.QPSK/OFDM多径时变信道仿真
最后
以上就是舒服白云最近收集整理的关于QPSK基础与多径信道Matlab仿真的全部内容,更多相关QPSK基础与多径信道Matlab仿真内容请搜索靠谱客的其他文章。








发表评论 取消回复