概述
模糊PID实现步骤及其MATLAB仿真与STM32程序实现
一：模糊PID相比传统PID的优点
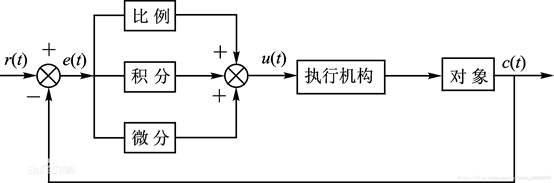
传统PID控制器自出现以来，凭借其结构简单、稳定性好、工作可靠、调整方便等优点成为工业控制主要技术。当被控对象的结构和参数具有一定的不确定性，无法对其建立精确的模型时，采用PID控制技术尤为方便。PID控制原理简单、易于实现，但是其参数整定异常麻烦。
对于传统的PID，其参数KP、KI、KD是根据开发者经验在某种特定环境下调试之后得到的一组接近最优的PID参数，然而对于一些非线性时变系统而言，其工作环境是时刻变化的，具有不确定性，如某执行器在海底工作就会收到不确定浪涌的干扰，而此时如果仍采用在设定环境下调节的一套固定PID参数，那么控制效果就会不好，严重情况下可能导致系统失效或者崩溃。
而模糊PID便可以在一定程度上解决这类问题，它利用模糊逻辑并根据一定的模糊规则对PID的参数进行实时的优化，以克服传统PID参数无法实时调整PID参数的缺点。
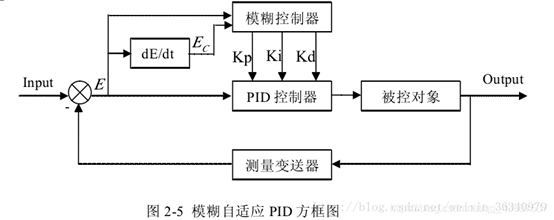
二：模糊PID的实现步骤
模糊PID一般包含以下6个步骤：
1.1、输入量的量化
输入数据都是精确的，要实现模糊算法需要现对其实现量化。所谓量化就是通过量化函数将输入量投射到一定的数字级别，一般都是相对于0对称的数字区间。具体投射到怎样的区间根据实际情况而定，因为这会直接影响到计算的精度。
例如：小车巡线时，会不断采集小车与轨迹线偏移的距离E，首是偏移的距离会有一个最大值，如-200到+200。我们可以将小车偏移的距离映射到-6到6的范围之间，-200即对应-6，200即对应6，故距离偏差都会被映射到-6到6的范围之间，除了距离E之外，我们还会采集以及当前距离偏差和上次距离偏差的变化（差值）EC（即此算法为2维输入，同理也可以是1维和3维，但2维更适合智能车），EC的变化范围是E的两倍是从-400到400，同理，我们也可以选择一个范围将其映射过去。
f(e)=(6e)/(Max-Min) f(ec)=(6ec)/(2(Max-Min))；其中6为设定的范围，后面模糊化会用到
1.2、模糊化
模糊化是模糊算法非常重要的一步，首先确定对应各语言变量的模糊子集，然后根据量化的结果，我们就可以判断该输入所属的集合并计算出对应的隶属度。计算隶属度的方法有很多，最常用的是使用三角形隶属度函数或梯形隶属度函数等来计算获得。
例如：将E和EC映射到-6到6的区间后，我们首先确定模糊子集：负大[NB]、负中[NM]、负小[NS]、零[ZO]、正小[PS]、正中[PM]、正大[PB]等7个语言变量就能够有足够精度表达其模糊子集。所以我们定义e和ec的模糊子集均为{NB，NM，NS，ZO，PS，PM，PB}。然后我们将E和EC的具体值与模糊集合对应上，如将NB定义为-6，NM定义为-4以此类推，PB对应与6。
最后我们确定e和ec在模糊子集上的隶属度。隶属度是一个介于0和1之间的值，用以描述对应一个输入属于某一个模糊自己的程度。一般我们描述成隶属度函数，可采用的隶属度函数很多，我们在次采用线性的隶属度函数，或者称为三角隶属度函数，其函数关系如下：
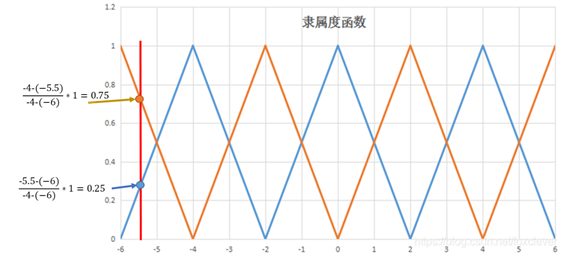
如：量化后的结果为-5.5，在-6和-4之间如果采用三角隶属度函数，则对应于-6（NB）的隶属度就是0.75，对应于-4（NM）隶属度就是0.25，但是他们相加为1，如果属于NB的隶属度为a，则属于NM的隶属度则为1-a。
1.3、规则库
规则库是基于控制量的模糊化而的味道的，是实现模糊推理的基础，很大程度上依赖于经验来完成。规则库的表现形式可以有多种，具体实现的形式根据我们实现的方便。
首先，我们来建立模糊规则库，在这里我们要对Kp、Ki和Kd三个参数进行调整，所以要建立这3个变量的模糊规则库。
在PID控制器中，Kp值的选取决定于系统的响应速度。增大Kp能提高响应速度，减小稳态偏差；但是，Kp值过大会产生较大的超调，甚至使系统不稳定减小Kp可以减小超调，提高稳定性，但Kp过小会减慢响应速度，延长调节时间。因此，调节初期应适当取较大的Kp值以提高响应速度，而在调节中期，Kp则取较小值，以使系统具有较小的超调并保证一定的响应速度；而在调节过程后期再将Kp值调到较大值来减小静差，提高控制精度。基于上述描述我们定义Kp的模糊规则如下：
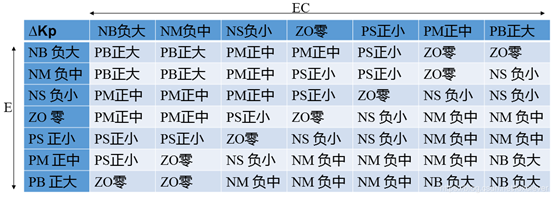
在系统控制中，积分控制主要是用来消除系统的稳态偏差。由于某些原因(如饱和非线性等)，积分过程有可能在调节过程的初期产生积分饱和，从而引起调节过程的较大超调。因此，在调节过程的初期，为防止积分饱和，其积分作用应当弱一些，甚至可以取零；而在调节中期，为了避免影响稳定性，其积分作用应该比较适中；最后在过程的后期，则应增强积分作用，以减小调节静差。依据以上分析，我们制定的Ki模糊规则如下：
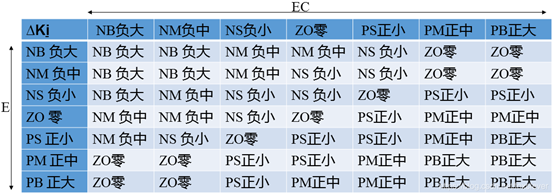
微分环节的调整主要是针对大惯性过程引入的，微分环节系数的作用在于改变系统的动态特性。系统的微分环节系数能反映信号变化的趋势，并能在偏差信号变化太大之前，在系统中引入一个有效的早期修正信号，从而加快响应速度，减少调整时间，消除振荡．最终改变系统的动态性能。因此，Kd值的选取对调节动态特性影响很大。Kd值过大，调节过程制动就会超前，致使调节时间过长；Kd值过小，调节过程制动就会落后，从而导致超调增加。根据实际过程经验，在调节初期，应加大微分作用，这样可得到较小甚至避免超调；而在中期，由于调节特性对Kd值的变化比较敏感，因此，Kd值应适当小一些并应保持固定不变；然后在调节后期，Kd值应减小，以减小被控过程的制动作用，进而补偿在调节过程初期由于Kd值较大所造成的调节过程的时间延长。依据以上分析，我们制定Kd的模糊规则如下：
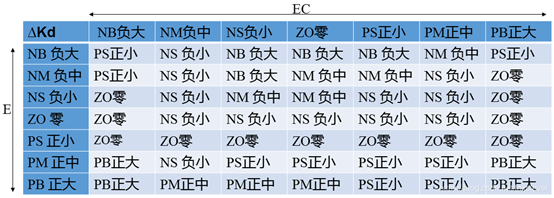1.4、模糊推理（解模糊）
对于采集回来的E和EC，我们可以知道他们占不同模糊集合的隶属度，也知道了模糊规则表，此时我们可以采用“重心法”根据模糊规则表去找出输出值所对应的隶属度。
我们假设为E的两个隶属度值为PM、PB,E属于PM的隶属度为a（a < 1），则属于PB的隶属度为（1 - a）。再假设EC的两个隶属度值为NB、NM，EC属于NM的隶属度为b，则属于NB的隶属度为（1 - b）。而在假设中，E属于PM的隶属度为a，EC属于NB的隶属度为( 1 - b )，则输出值属于ZO的隶属度为a *( 1 - b )（看图）。
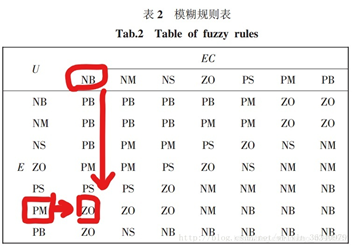同理我们可以得出，当输出值属于ZO的另外两个隶属度为a * b， （ 1 - a ） * （ 1 - b） ，而输出值属于NS的隶属度为（ 1 - a ） * 1 - b。
在这里我们先证明一个条件，将这四个隶属度加起来，刚好等于1。这是因为
（a + （1 - a）） * （b + （1 - b）） = a * b + ( 1 - a ) * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) （下图）
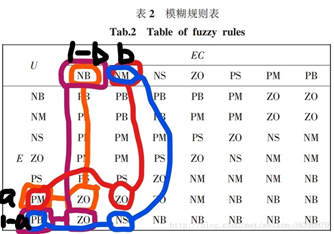
即一个十字相乘的概念。这个等式说明输出值的隶属度之和等于1（第三步求解的时候需要用到隶属度之和）。
因此，我们知道了输出值为ZO的隶属度和为 a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ，输出值为NS的隶属度为 ( 1 - a ) * b 。
1.5、清晰化
对于输出值，我们同样采用给予隶属度的办法。例如，我们把输出值KI、KI、KD同样选择不同的论域划分为不同的模糊集合（其实这一步在制定模糊规则的时候已经做了），如KP选择为（-9，9）的论域，-9为NB，-6为NM，-3为NS，0为ZO(ZE)，3为PS，6为PM，9为PB。有部分文章是将输出定义为ΔKP，ΔKI，ΔKD，如果是这样可以将输出论域的范围缩小点，然后做PID计算的时候在原来参数的基础上加上增量值即可。具体哪种方式好，作者还没有验证，欢迎读者留言指教。
根据上一步所得出的结论，我们就可以用隶属度乘以相应的隶属值算出输出值的解，即 （a * b + a * ( 1 - b ) + ( 1 - a ) * ( 1 - b ) ） * ZO + ( 1 - a ) * b * NS。到此为止，整个模糊过程就结束了。
1.6、工程量化
系统控制输出是一个精确的数，但不是可以直接用于对象控制的物理量，所以在最后还要按照我们的需要进行转换。比如对应PID的参数则可进行必要的转换和修正再输出给PID控制器。
三：模糊PID的MATLAB仿真
1：在MATLAB中输入fuzzy打开Fuzzy Logic Designer
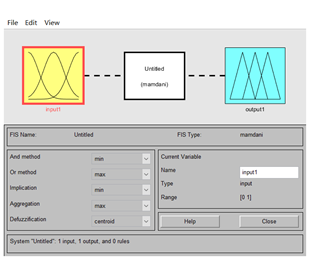其中input1为输入，右下角可以改变输入值的名称，一般为E和EC，mamdani为模糊规则，双击即可设置模糊规则，output1为输出。
2：请自行浏览菜单栏，可以看到导入(import)、导出(export)、添加输入/输出变量(add variable)、查看规则(rules)和生成的曲面(surface)。
请根据设计添加输入E、EC和输出KP、KI、KD
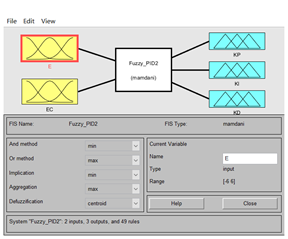
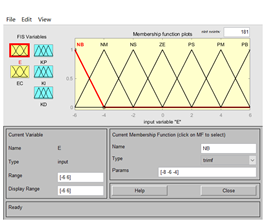
3：双击输入可以增加隶属度函数曲线（add MF：一次性添加多条）（add Cusom MF：添加一条，并在添加的时候修改曲线的类型以及曲线的范围），一般选择trimf三角隶属度曲线，根据之前讲述的论域设计隶属度曲线，并修改名称。
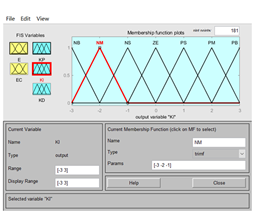
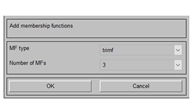
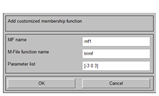
4：将输入、输出的隶属度曲线和范围设定好之后，设计模糊规则库，双击mamdani即添加，根据上述说明的模糊规则库逐行添加。
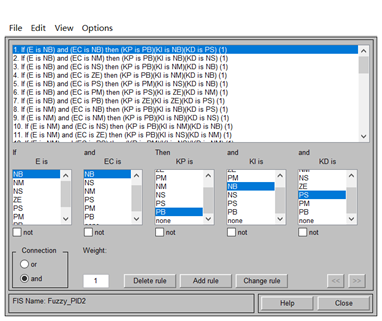
5：添加完之后点击View-Rules和Surfaces即可查看该模糊控制器的属性：
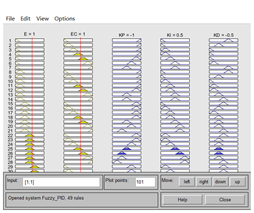
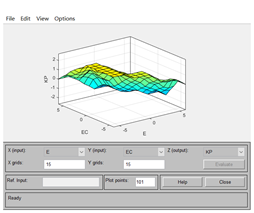
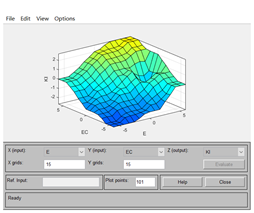
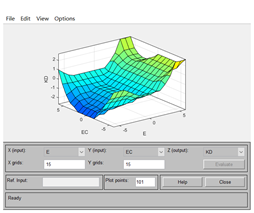
上述规则和曲面可理解为：当E和EC为某值时，输出量对应的是哪一个值。
5：导入工作空间
关闭规则编辑器。单击 file-> export -> To file… 命名为Fuzzy_PID.fis -> 保存。
单击 File -> Export -> To workspace -> OK。
我们会发现在MATLLAB的工作区（Workspace）有来了一个1*1 struct的值。
6：simulink仿真
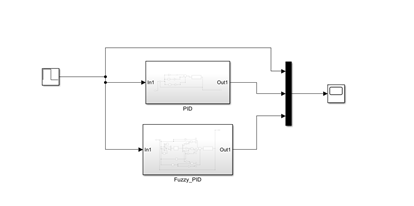传统PID
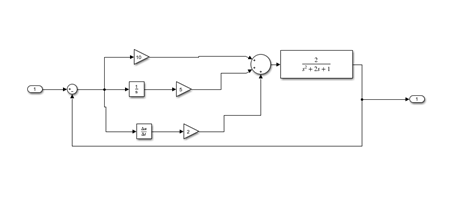
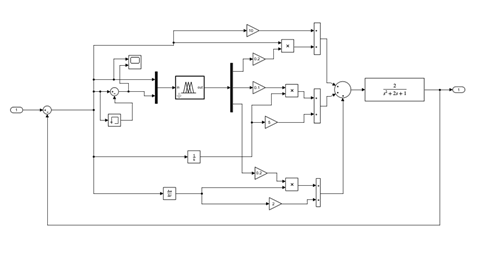
模糊PID：
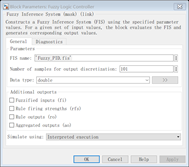
选择模糊控制器时，要确认FIS name加载的文件在工作空间和工作目录之下
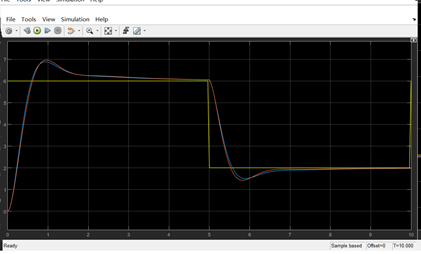
控制效果比较：调参是一个比较费时间的事情，笔者没有完全调好，读者可以多花点时间自行调整。
四：STM32程序实现
fuzzypid.h
#ifndef __FUZZYPID_H
#define __FUZZYPID_H
#include "pid.h"
//定义模糊PID结构体
typedef struct
{
float setVaule; //设定值
float deta_kp; //比例值增量
float date_ki; //积分值增量
float date_kd; //微分值增量
float lasterror; //前一拍偏差
float preerror;//前二拍偏差
float maximum; //输出值的上限
float minimum; //输出值的下限
float qKp; //kp增量的修正系数
float qKi; //ki增量的修正系数
float qKd; //kd增量的修正系数
}FUZZYPID;
//外部文件可见
extern FUZZYPID FPID;
//模糊PID计算
void Fuzzytrans(float _Set_Vaule,float _Measure_Vaule,float pre_Measure_Vaule);
#endif
fuzzypid.c
#include "fuzzypid.h"
#include "pid.h"
#define NB -6
#define NM -4
#define NS -1
#define ZO 0
#define PS 1
#define PM 4
#define PB 6
//规则库
static const float ruleKp[7][7]={
PB, PB, PM, PM, PS, PS, ZO,
PB, PB, PM, PM, PS, ZO, ZO,
PM, PM, PM, PS, ZO, NS, NM,
PM, PS, PS, ZO, NS, NM, NM,
PS, PS, ZO, NS, NS, NM, NM,
ZO, ZO, NS, NM, NM, NM, NB,
ZO, NS, NS, NM, NM, NB, NB
};
static const float ruleKi[7][7]={
NB, NB, NB, NM, NM, ZO, ZO,
NB, NB, NM, NM, NS, ZO, ZO,
NM, NM, NS, NS, ZO, PS, PS,
NM, NS, NS, ZO, PS, PS, PM,
NS, NS, ZO, PS, PS, PM, PM,
ZO, ZO, PS, PM, PM, PB, PB,
ZO, ZO, PS, PM, PB, PB, PB
};
static const float ruleKd[7][7]={
PS, PS, ZO, ZO, ZO, PB, PB,
NS, NS, NS, NS, ZO, NS, PM,
NB, NB, NM, NS, ZO, PS, PM,
NB, NM, NM, NS, ZO, PS, PM,
NB, NM, NS, NS, ZO, PS, PS,
NM, NS, NS, NS, ZO, PS, PS,
PS, ZO, ZO, ZO, ZO, PB, PB
};
初始化结构体参数
FUZZYPID FPID={
0,0,0,0,0,0,
0,0,1,1,1
};
//隶属度计算函数
static void CalcMembership(float *ms,float qv,int * index)
{
if((qv>=NB)&&(qv<NM))
{
index[0]=0;
index[1]=1;
ms[0]=-0.5*qv-2.0; //y=-0.5x-2.0
ms[1]=0.5*qv+3.0; //y=0.5x+3.0
}
else if((qv>=NM)&&(qv<NS))
{
index[0]=1;
index[1]=2;
ms[0]=-0.5*qv-1.0; //y=-0.5x-1.0
ms[1]=0.5*qv+2.0; //y=0.5x+2.0
}
else if((qv>=NS)&&(qv<ZO))
{
index[0]=2;
index[1]=3;
ms[0]=-0.5*qv; //y=-0.5x
ms[1]=0.5*qv+1.0; //y=0.5x+1.0
}
else if((qv>=ZO)&&(qv<PS))
{
index[0]=3;
index[1]=4;
ms[0]=-0.5*qv+1.0; //y=-0.5x+1.0
ms[1]=0.5*qv; //y=0.5x
}
else if((qv>=PS)&&(qv<PM))
{
index[0]=4;
index[1]=5;
ms[0]=-0.5*qv+2.0; //y=-0.5x+2.0
ms[1]=0.5*qv-1.0; //y=0.5x-1.0
}
else if((qv>=PM)&&(qv<=PB))
{
index[0]=5;
index[1]=6;
ms[0]=-0.5*qv+3.0; //y=-0.5x+3.0
ms[1]=0.5*qv-2.0; //y=0.5x-2.0
}
}
//输入值的量化论域(-6->6)
static void LinearQuantization(FUZZYPID *vPID,float _Real_Value,float *qValue)
{
float thisError;
float deltaError;
thisError=vPID->setVaule-_Real_Value; //计算当前偏差
deltaError=thisError-vPID->lasterror; /计算偏差增量
//E和EC的量化
qValue[0]=6.0*thisError/(vPID->maximum-vPID->minimum);
qValue[1]=3.0*deltaError/(vPID->maximum-vPID->minimum);
}
//解模糊
static void FuzzyComputation (FUZZYPID *vPID,float _Real_Value)
{
//量化值
float qValue[2]={0,0};
int indexE[2]={0,0}; //e在规则库中的索引
float msE[2]={0,0}; //e的隶属度
int indexEC[2]={0,0}; //ec在规则库中的索引
float msEC[2]={0,0}; //ec的隶属度
//pid增量值
float pidvalue[3];
//量化
LinearQuantization(vPID,_Real_Value,qValue);
//计算e的隶属度和索引
CalcMembership(msE,qValue[0],indexE);
//计算ec的隶属度和索引
CalcMembership(msEC,qValue[1],indexEC);
//采用重心法计算pid增量值
pidvalue[0]=msE[0]*(msEC[0]*ruleKp[indexE[0]][indexEC[0]]+msEC[1]*ruleKp[indexE[0]][indexEC[1]])
+msE[1]*(msEC[0]*ruleKp[indexE[1]][indexEC[0]]+msEC[1]*ruleKp[indexE[1]][indexEC[1]]);
pidvalue[1]=msE[0]*(msEC[0]*ruleKi[indexE[0]][indexEC[0]]+msEC[1]*ruleKi[indexE[0]][indexEC[1]])
+msE[1]*(msEC[0]*ruleKi[indexE[1]][indexEC[0]]+msEC[1]*ruleKi[indexE[1]][indexEC[1]]);
pidvalue[2]=msE[0]*(msEC[0]*ruleKd[indexE[0]][indexEC[0]]+msEC[1]*ruleKd[indexE[0]][indexEC[1]])
+msE[1]*(msEC[0]*ruleKd[indexE[1]][indexEC[0]]+msEC[1]*ruleKd[indexE[1]][indexEC[1]]);
//pid增量修正
vPID->deta_kp=vPID->qKp*pidvalue[0];//Êä³öÏÞ·ù ÖµÓ³É䵽ʵ¼Ê¿Õ¼ä
vPID->date_ki=vPID->qKi*pidvalue[1];
vPID->date_kd=vPID->qKd*pidvalue[2];
}
/*程序入口主函数*/
void Fuzzytrans(float _Set_Vaule,float _Measure_Vaule,float pre_Measure_Vaule)
{
FPID.setVaule=_Set_Vaule;
//上一次的偏差值
FPID.lasterror=_Set_Vaule-pre_Measure_Vaule;
//修正系数
FPID.qKp=1;
FPID.qKi=1;
FPID.qKi=1;
//输入量的最大最小值
FPID.maximum=8000;
FPID.minimum=0;
FuzzyComputation(&FPID,_Measure_Vaule);
}
参考博客：
【1】https://blog.csdn.net/qq_41913616/article/details/82020685
【2】https://blog.csdn.net/foxclever/article/details/83932107
【3】https://blog.csdn.net/m0_37763336/article/details/89325795
【4】https://blog.csdn.net/Junhanie/article/details/107809835
最后
以上就是还单身发夹为你收集整理的模糊PID实现步骤及其MATLAB仿真与STM32程序实现的全部内容，希望文章能够帮你解决模糊PID实现步骤及其MATLAB仿真与STM32程序实现所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复