模糊控制(一)模糊控制简介及数学基础
模糊集合、隶属度、模糊推理
O、概念
一些概念在特定的场合有一定的外延,如国家、货币、法定年龄等,对于这些明确的概念,在数学中常用经典集合来描述;
还有一些概念在一些场合没有明确的外延,如年龄大小、冷与热、风的强弱等,对于这些不明确的概念,我们称之为模糊概念,在数学上用模糊集合来描述。

一、简介
1.模糊性与随机性的区别
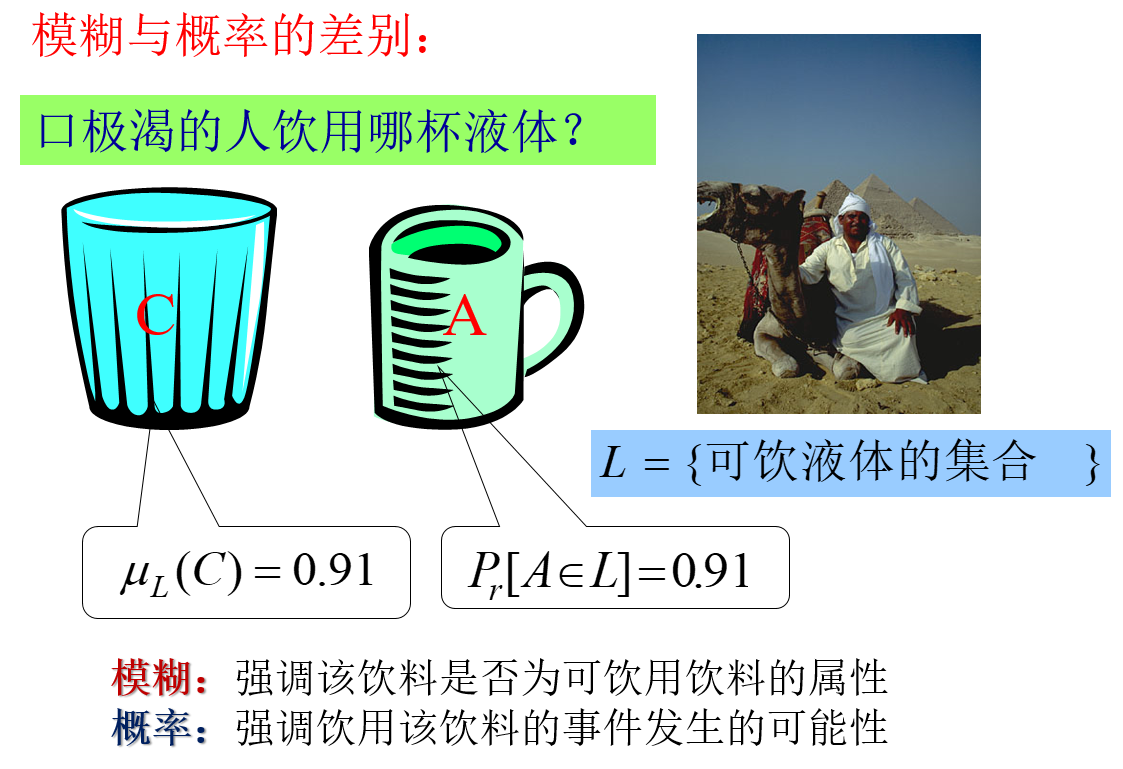
模糊集合研究的是不确定性,这种不确定性是事物本身形态和类属的不确定性;另一种随机性是在事件是否发生的表现出来的不确定性,而事件本身的形态和类属是确定的。举个例子:
2.模糊控制的特点
- 不需要知道被控对象的数学模型;
- 与人类脑类活动的特点一致:模糊性(高中低大小等等定性词汇)、经验性(模糊控制核心是模糊规则,模糊控制中的只是表示、模糊规则和推理均建立在人的成熟经验之上);
- 易构造(单片机、工业计算机、专用模糊控制芯片等均可以构造);
- 鲁棒性好 (可适用于模型参数不确定或波动较大的线性和非线性系统的控制)。
二、模糊控制的数学基础——模糊集合
1.模糊集合


2.隶属度

隶属度具有人为主观性,根据实际情况设定,就是工程中的调参。
3.模糊集合的数学表示
X为离散论域
向量表示法

Zadeh表示法

序偶表示法

4.模糊集合的相关概念
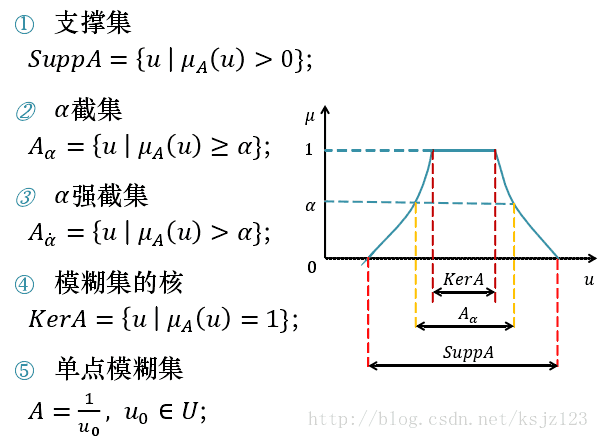
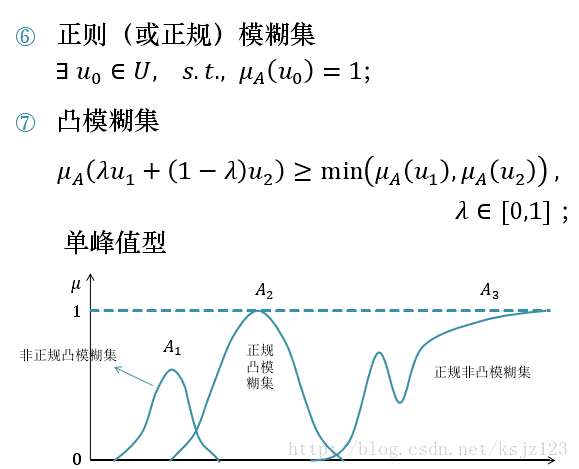
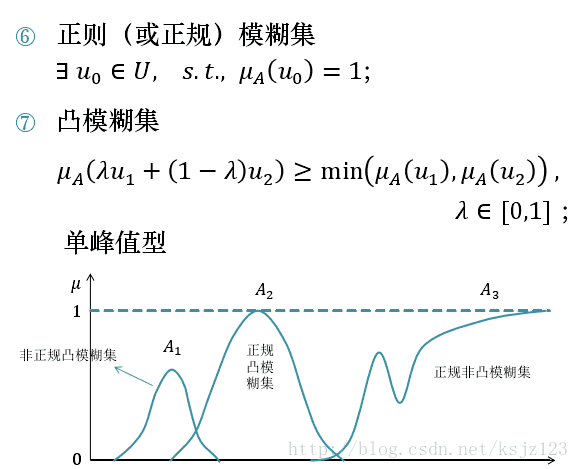
5.模糊集合的运算


不难看出,代数积和代数和是一对运算形式,有界积和有界和为一对运算形式,这两对模糊集运算各有长短。在模糊信息的表达和处理中究竟选用哪一种要根据实际的要求,通过实践加以证明。

6.隶属函数
- 普通集合用特征函数来刻画,模糊函数用隶属函数作定量描述;
- 特征函数的值域为{0,1},隶属函数的值域为区间【0,1】;
- 隶属函数是特征函数的拓展和一般化。
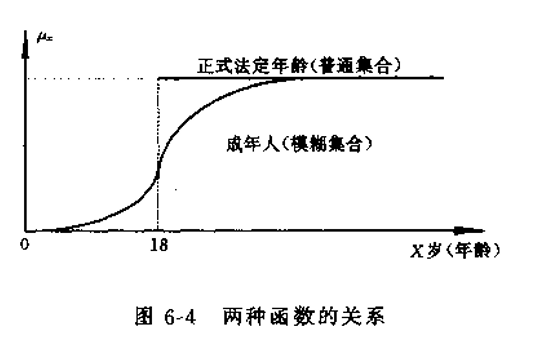
常用的隶属函数形状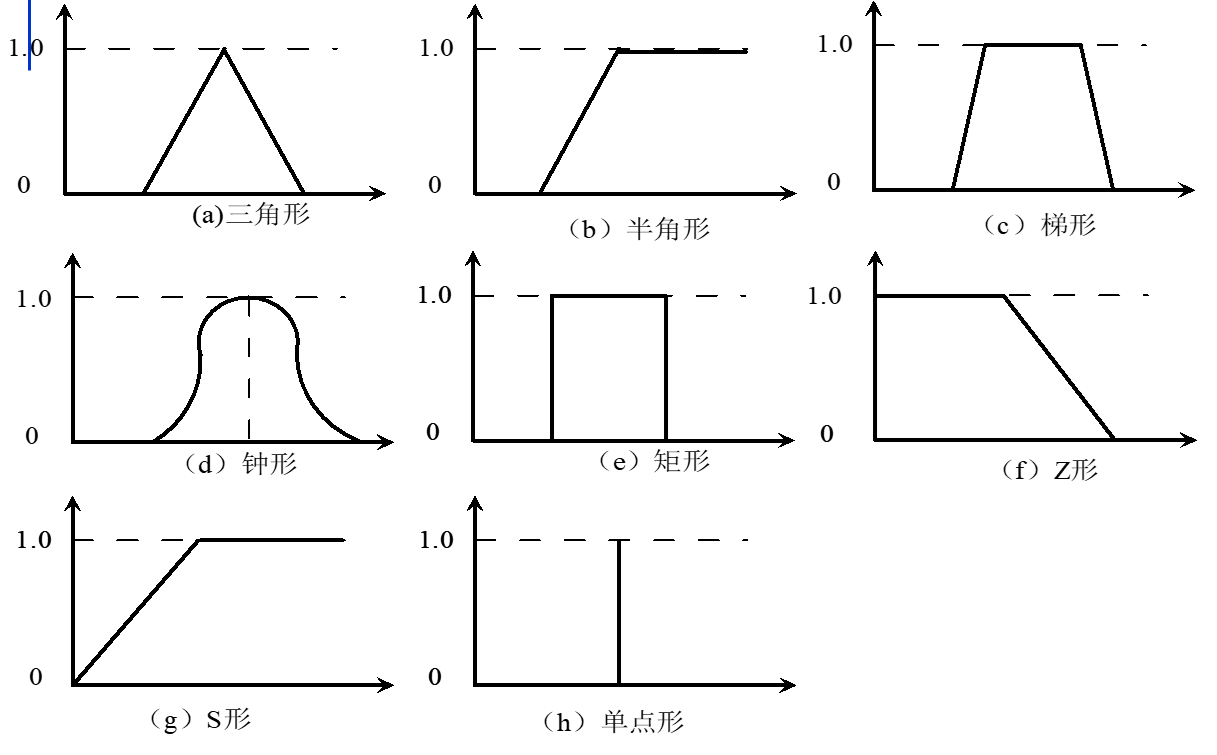
7.模糊关系的合成
由A集合和B集合之间的模糊关系及B集合和C集合之间的模糊关系得到A集合和B集合之间的模糊关系的一种运算。
三、模糊推理
1.概念
三段论:大前提——>小前提——>结论
模糊推理:又称模糊逻辑推理,是指已知模糊命题(包括大前提和小前提),推出心得模糊命题作为结论的过程。
2.推理方法
常用的推理方法有:
- Zadeh推理方法
- Mamdani推理方法
- 多输入推理方法(最常用)
- 多输入多规划推理
多输入模糊推理


下文:模糊控制(二)模糊控制——模糊推理
最后
以上就是大力篮球最近收集整理的关于模糊控制(一)模糊控制简介及数学基础的全部内容,更多相关模糊控制(一)模糊控制简介及数学基础内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复