LSTM基本理论及手写数字识别实战应用（pytorch）

66 阅读 0 评论 44 点赞

我是靠谱客的博主还单身发夹，最近开发中收集的这篇文章主要介绍LSTM基本理论及手写数字识别实战应用（pytorch），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

LSTM介绍

LSTM的特点（与RNN的区别）

特点：加入一个门控机制，该被记住的信息会一直传递，不该记的会被“门”阶段。由三个具有sigmoid激活函数的全连接层处理，以计算输入门、遗忘门和输出门的值。因此，这三个门的值都在（0，1）的范围内。

LSTM的关键就是细胞状态，水平线在图上方贯穿运行，细胞状态类似于传送带。直接在整个链上运行，只有少量的线性交互，信息在上面流传保持不变会很容易。

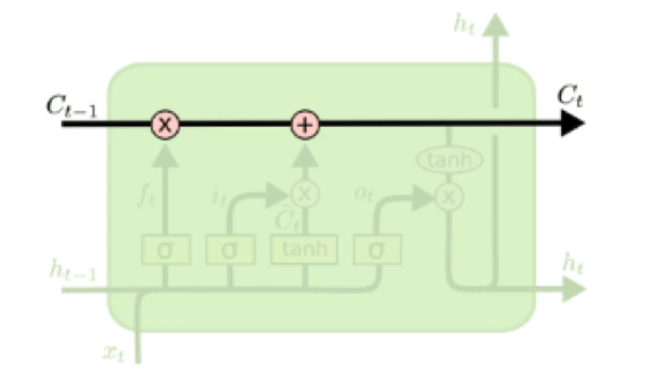
在这里插入图片描述

LSTM通过门结构来去除或增加信息到细胞状态的能力。是一种让信息选择通过的方法。包含一个sigmoid神经网络和一个点乘操作，其中，sigmoid输出0-1的数值，描述每个部分有多少量可以通过，0表示不允许任何量通过，1表示允许任意量通过。（LSTM通过三个门来保护和控制细胞状态）

具体实现流程

第一步：

cell state是否传递到下一个cell state 是通过sigmoid layer (遗忘门) 决定的。sigmoid后结果为0/1，1表示保留cell state, 0表示遗忘以前记忆的数据
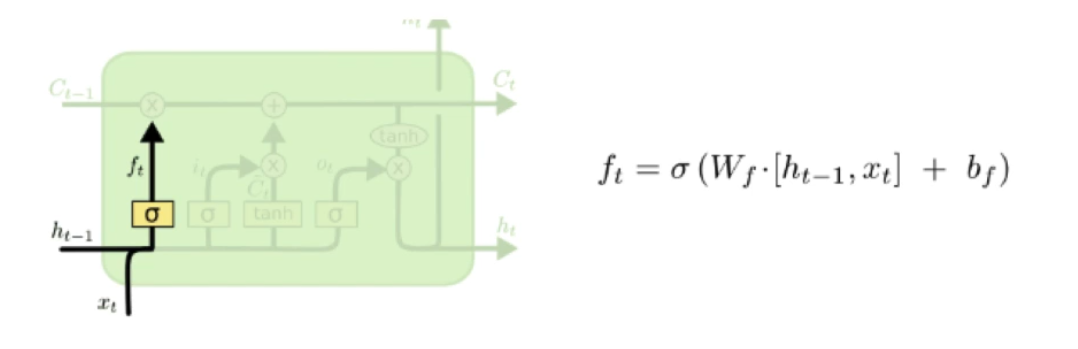
在这里插入图片描述

第二步：

也是一个sigmoid layer被成为输入门（it），决定了我们需要更新哪些值，还有有一个tanh layer用来制造新的候选值向量(Ct)，最后将it和Ct进行点乘。
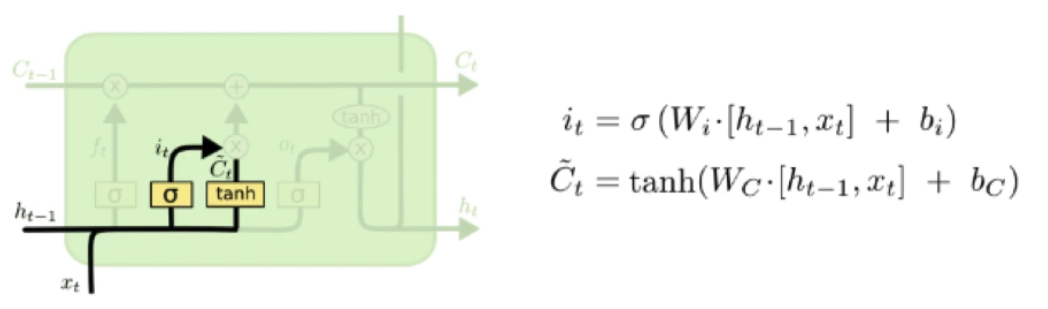
在这里插入图片描述

第三步：

ft,抛弃需要忘记的之前的信息，然后加上我们需要记录的信息。如下式所示，ft*Ct-1表示的含义为，忘记上一层的部分单元状态。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RwFWJ2Bi-1649292695221)(C:UserspcAppDataRoamingTyporatypora-user-imagesimage-20220402120114657.png)]

第四步：

最后决定，哪些需要被输出，这些输出是基于cell state的。用sigmoid layer决定应该输出哪一部分cell state.将单元状态放入tanh函数中使得结果处于（-1，1）区间中。并将tanh(Ct)与输出部分Ot相乘，以此控制我们想要输出的部分。

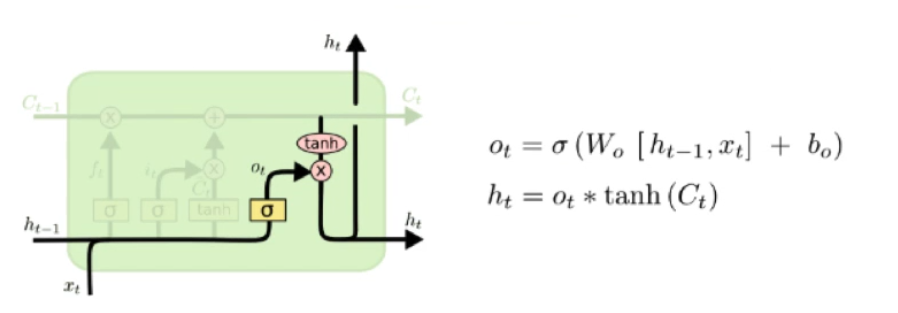
公式汇总及总结

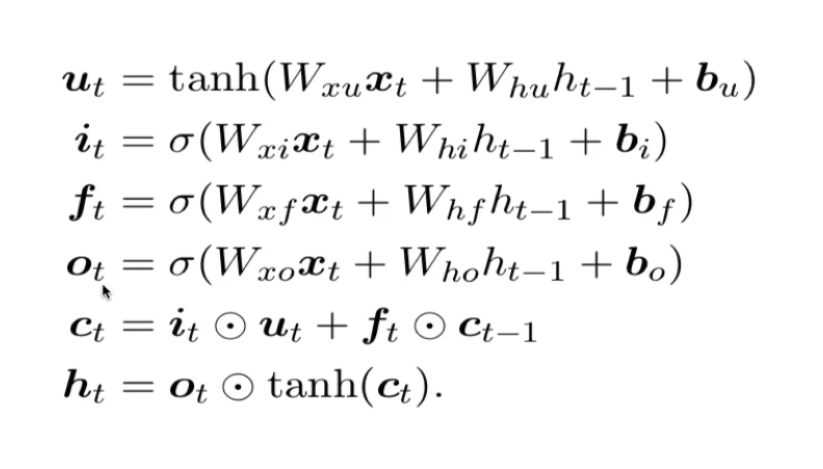
在这里插入图片描述

ht是t时刻隐藏层状态，Ct是t时刻的单元状态，xt是输入值

it,ft,ot是输入、遗忘、输出门

关于LSTM的认识：LSTM神经元在时间维度上向后传递了两份信息:cell state和hidden state。

hidden state是cell state经过一个神经元和一道输出门后得到的，因此hidden state里包含的记忆，实际上是cell state衰减之后的内容。另外，cell state在一个衰减较少的通道里沿时间轴传递，对时间跨度较大的信息的保持能力比hidden state要强很多。

因此，实际上hidden state里存储的，主要是近期记忆；cell state里存储的，主要是远期记忆。cell state的存在，使得LSTM得以对长依赖进行很好地刻画。（过去的信息直接在Cell运行，当下的决策或者说特征选择在Hidden State里面运行）

LSTM实现手写数字识别（pytorch代码）

这里仅仅是将LSTM应用于手写数字识别（图像的处理）这一经典问题，体现网络结构和训练过程方便大家学习，实际上RNN、LSTM等网络一般用于处理序列问题，而CNN等网络被用来处理图像问题（可以保存空间特征）

导入环境

import torch
from torch import nn
import torchvision.datasets
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
import warnings
import numpy as np
warnings.filterwarnings('ignore')
torch.manual_seed(1)

定义超参数

epoch = 2
batch_size = 64
time_step = 28 #时间步数（图片高度）（因为每张图像为28*28，而每一个序列长度为1*28，所以总共是28个1*28）
input_size = 28 #每步输入的长度（每行像素的个数）
lr = 0.01
download_mnist = True

num_classes = 10 #总共有10类
hidden_size = 128 #隐层大小
num_layers = 1

训练和测试数据定义

#MINIST
train_data = torchvision.datasets.MNIST(
    root='./mnist',
    train=True,
    transform=torchvision.transforms.ToTensor(),
    download=download_mnist,
)

test_data = torchvision.datasets.MNIST(
    root='./mnist',
    train=False,
    transform=torchvision.transforms.ToTensor(),
    download=download_mnist,
)

print(train_data.train_data.size())
print(train_data.train_labels.size())
plt.imshow(train_data.train_data[0].numpy(), cmap='gray')
plt.title("MNIST:%i" % train_data.train_labels[0])
plt.show()

torch.Size([60000, 28, 28])
torch.Size([60000])

加载器数据处理：

train_loader = torch.utils.data.DataLoader(dataset=train_data, batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(dataset=test_data, batch_size=batch_size, shuffle=False)

data = next(iter(train_loader)) #train_loader是迭代器
print(data[0].shape)  #data的第一个元素为64个（1*28*28的图像）
print(data[1].shape)  #data的第二个元素为64个标签
# print("data[0]", data[0])
# print("data[1]", data[1])
print(np.array(data).shape)
#每次迭代为64张图片由batch_size决定， 1为通道数（灰白图片）

torch.Size([64, 1, 28, 28])
torch.Size([64])
(2,)

for step, (b_x, b_y) in enumerate(train_loader): #遍历数据和标签
    print(b_x.shape)
    b_x = b_x.view(-1, 28, 28)  #将tensor拉成(64*28*28)
    print(b_x.shape)
    print(b_y.shape)
    
    print(b_x[0].shape)
    print(b_y[0])
    break

torch.Size([64, 1, 28, 28])
torch.Size([64, 28, 28])
torch.Size([64])
torch.Size([28, 28])
tensor(9)

test_data = torchvision.datasets.MNIST(root='./mnist/', train=False, transform=transforms.ToTensor())
test_x = test_data.test_data.type(torch.FloatTensor)[:2000]/255
test_y = test_data.test_labels.numpy()[:2000]
print(test_x.shape)
print(test_y.shape)

torch.Size([2000, 28, 28])
(2000,)

定义LSTM模型

(input0, output0) -> LSTM -> (output0, state1)
(input1, output1) -> LSTM -> (output1, state2)
…
(inputN, outputN) -> LSTM -> (outputN, stateN+1)
outputN -> Lineaer -> prediction
通过LSTM分析每一刻的值，并且将这一时刻和前面时刻的理解合并在一起，生成当前时刻对前面数据的理解或记忆

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers, num_classes):
        
        super(RNN, self).__init__()
        
        #LSTM层
        self.rnn_layer = nn.LSTM(
            input_size=input_size,  #每行的像素点个数
            hidden_size=hidden_size,
            num_layers=num_layers, #层数
            batch_first=True,  #input和output会以batch_size为第一维度   
        )
        
        #输出层
        self.linear_layer = nn.Linear(hidden_size, num_classes)
    
    def forward(self, x):
        #x.shape (batch, time_step, input_size)
        #rnn_out.shape (batch, time_step, output_size)
        #h_n (n_layers, batch, hidden_size) LSTM有两个hidden states, h_c是分线， h_c是主线
        #c_n (n_layers, batch, hidden_size)
        rnn_output, (h_n, c_n) = self.rnn_layer(x, None) #None表示hidden state 会用全0的state
        #选择lstm_output[-1] 也就是最后一个输出，因为每个cell都会有输出，但我们只关心最后一个(分类问题)
        #选取最后一个时间节点的rnn_output输出
        #这里的 rnn_output[:, -1, :]的值也是h_n的值
        output = self.linear_layer(rnn_output[:, -1, :])
        return output

rnn = RNN(input_size, hidden_size, num_layers, num_classes)
print(rnn)

RNN(
  (rnn_layer): LSTM(28, 128, batch_first=True)
  (linear_layer): Linear(in_features=128, out_features=10, bias=True)
)

LSTM模型训练和预测

#定义优化器和损失函数
optimizer = torch.optim.Adam(rnn.parameters(), lr=lr)
loss_func = nn.CrossEntropyLoss()
# device = 'cuda' if torch.cuda.is_available() else 'cpu'
# rnn.to(device) #将模型送入cuda
# print('devices = ', device)

在分类问题中，通常需要使用max()函数对softmax函数的输出值进行操作，求出预测值索引，然后与标签进行比对，计算准确率。
函数：
output = torch.max(input, dim)
输入:
input是softmax函数输出的一个tensor
dim是max函数索引的维度0/1，0是每列的最大值，1是每行的最大值
输出:
函数会返回两个tensor，第一个tensor是每行的最大值；第二个tensor是每行最大值的索引。

# print(len(train_loader))
#训练流程
for i in range(epoch):
    rnn.train()
    total_batch = len(train_loader)
    run_loss = 0.0
    for step, (images, labels) in enumerate(train_loader):
#         images, labels = images.to(device), labels.to(device)
        images = images.view(-1, 28, 28)
        
        #运行模型
        outputs = rnn(images)
        #损失函数
        loss = loss_func(outputs, labels)
        #清除梯度
        optimizer.zero_grad()
        #反向传播
        loss.backward()
        #更新
        optimizer.step()
        
        run_loss = loss.item()
        
        if(step + 1) % 100 == 0:
            print('Epoch[{}/{}], step[{}/{}], train_loss:{}'.format(i+1, epoch, step+1, total_batch, '%.4f' % run_loss))
    #训练结束
    
    
    #对模型进行测试
    with torch.no_grad():
        rnn.eval()
        correct = 0
        total = 0
        for i, (images, labels) in enumerate(test_loader):
#             images, labels = images.to(device), labels.to(device)
            images = images.view(-1, 28, 28)
            outputs = rnn(images)   #output(64, 10)  输出为（batch_size, output_size） 因为我们只关心最后一维输出
            #输出是每一批64个样本，每个样本有10个概率值（对应十个分类） 将概率值最大数值的所在类作为当前的预测结果
            if i == 0:
                print("输出的结果", )
                print("输出的维度", outputs.shape)
            _, prediction = torch.max(outputs.data, 1)  #prediction保存最大值的索引,也就相当于标签数0-9
            if i == 0:
                print("最大值和索引", (_, prediction))
            total += labels.size(0)
            correct += (prediction == labels).sum().item()
        #输出结果
        print(total, correct)
        print("Test accuracy of model in test images:{}".format(correct/total))

torch.save(rnn.state_dict(), 'rnn.pkl')

训练结果：

Epoch[1/2], step[100/938], train_loss:0.8388
Epoch[1/2], step[200/938], train_loss:0.5867
Epoch[1/2], step[300/938], train_loss:0.2973
Epoch[1/2], step[400/938], train_loss:0.2541
Epoch[1/2], step[500/938], train_loss:0.0706
Epoch[1/2], step[600/938], train_loss:0.1402
Epoch[1/2], step[700/938], train_loss:0.2660
Epoch[1/2], step[800/938], train_loss:0.1185
Epoch[1/2], step[900/938], train_loss:0.1742
输出的结果
输出的维度 torch.Size([64, 10])
最大值和索引 (tensor([ 8.9605,  7.0959, 10.5307,  6.7607,  6.3854,  9.9979,  5.8245,  4.1132,
         5.9978,  4.8795,  9.1994,  9.8002,  7.5107,  6.8908,  9.3948,  6.6050,
         6.8807,  9.0425,  3.7695,  6.1420,  2.9081,  9.6258,  9.2399,  7.6210,
         5.8143,  7.2229,  7.2480,  6.2991,  8.4457,  9.9901,  7.3378, 10.5309,
         6.9480,  3.4193,  7.5618,  6.5634,  7.3954,  9.9699,  4.1137,  9.4361,
         9.4986,  7.1948,  5.9212,  3.2806,  6.1133,  6.3882,  7.0285,  7.2906,
         5.1487,  6.1292, 10.3341,  5.6718,  7.6015,  5.9462, 10.0196,  6.7889,
         6.5652, 10.1855,  6.0312,  4.4976,  7.1902,  3.6839,  3.4036,  4.0903]), tensor([7, 2, 1, 6, 4, 1, 4, 9, 6, 9, 0, 6, 9, 0, 1, 5, 9, 7, 3, 4, 5, 6, 6, 5,
        4, 0, 7, 4, 0, 1, 3, 1, 3, 4, 7, 2, 7, 1, 2, 1, 1, 7, 4, 2, 3, 5, 1, 2,
        4, 4, 6, 3, 5, 5, 6, 0, 4, 1, 9, 5, 7, 8, 5, 2]))
10000 9490
Test accuracy of model in test images:0.949
Epoch[2/2], step[100/938], train_loss:0.1428
Epoch[2/2], step[200/938], train_loss:0.0757
Epoch[2/2], step[300/938], train_loss:0.0949
Epoch[2/2], step[400/938], train_loss:0.1465
Epoch[2/2], step[500/938], train_loss:0.0187
Epoch[2/2], step[600/938], train_loss:0.0690
Epoch[2/2], step[700/938], train_loss:0.1198
Epoch[2/2], step[800/938], train_loss:0.1921
Epoch[2/2], step[900/938], train_loss:0.0716
输出的结果
输出的维度 torch.Size([64, 10])
最大值和索引 (tensor([ 7.3178, 10.6847,  9.3740,  9.1583,  8.6876,  9.2710,  8.7351,  7.1284,
         3.9576,  8.4149, 10.2904,  6.8698,  8.2608,  8.7133,  9.3011, 10.0828,
         7.2414,  7.4259,  3.6580,  9.1079,  8.4237,  8.2516,  7.3270,  9.8116,
         8.6081, 10.0169,  6.0650,  8.7936,  9.6732,  5.8133, 10.1085,  5.3593,
        10.7706,  4.9747,  6.7490, 10.1497,  7.4211,  5.8098,  7.0112, 10.3313,
         6.5496,  7.1471,  7.7012,  6.9186,  9.2815,  8.7697,  7.8598,  9.9610,
         6.2150,  8.2662,  7.9309,  8.6589,  9.6622,  8.4956,  5.3241,  8.6748,
         8.7984,  8.1394,  6.9538,  5.7582,  9.1990,  7.1813,  4.1776,  7.4175]), tensor([7, 2, 1, 0, 4, 1, 4, 9, 5, 9, 0, 6, 9, 0, 1, 5, 9, 7, 3, 4, 9, 6, 6, 5,
        4, 0, 7, 4, 0, 1, 3, 1, 3, 4, 7, 2, 7, 1, 2, 1, 1, 7, 4, 2, 3, 5, 1, 2,
        4, 4, 6, 3, 5, 5, 6, 0, 4, 1, 9, 5, 7, 8, 9, 3]))
10000 9794
Test accuracy of model in test images:0.9794