浮点数精度丢失分析及解决为什么会出现精度丢失浮点数底层存储实现浮点数操作如何避免精度丢失参考

77 阅读 0 评论 51 点赞

我是靠谱客的博主单身高跟鞋，最近开发中收集的这篇文章主要介绍浮点数精度丢失分析及解决为什么会出现精度丢失浮点数底层存储实现浮点数操作如何避免精度丢失参考，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

Java语言在处理浮点数，其实现逻辑与整数不同，如果使用不当可能会造成精度丢失、计算不准确、死循环等问题，严重的话，会造成经济损失。本文将从浮点数精度丢失入手，详细介绍下浮点数的原理及使用。

为什么会出现精度丢失

计算机使用二进制存储数据，由于二进制自身局限性，导致其无法精确的表示所有小数。而浮点数是由整数部分和小数部分组成，这也就意味着，计算机无法精确表示浮点数。也即，在计算机中，浮点数存在精度丢失的问题。这里将以十进制小数转为二进制数为例，介绍下为何二进制无法精确表示小数。
十进制小数转换成二进制小数采用"乘2取整，顺序排列"的做法。基本思想如下：用二乘以当前十进制小数，然后将乘积的整数部分取出，如果乘积中的小数部分为零或者达到所要求的精度则停止计算。否则再用二乘以余下的小数部分，又得到一个乘积，再将积的整数部分取出，如此进行。完成计算后，把每次执行取出的整数部分按顺序排列起来，先取的整数作为二进制小数的高位有效位，后取的整数作为低位有效位。这里介绍下如何把十进制小数0.8125转换为二进制小数。
0.8125转二进制.png
当然，也存在无法准确适用二进制表示的小数。如十进制小数0.7。
0.7转二进制.png
对于无法用二进制表示的小数，只能根据精度近似的表示。

浮点数底层存储实现

与整数存储数值不同，浮点数在计算机的存储时，会拆分成是三个部分：符号位、指数位、尾数位。其抽象公式是：
$1)^S*(1.M...)*2^E$
其中， $S$ 表示符号(正数、负数)、E表示指数、M表示尾数。在Java中，float是32位存储，double是64存储，各部分的存储长度是：
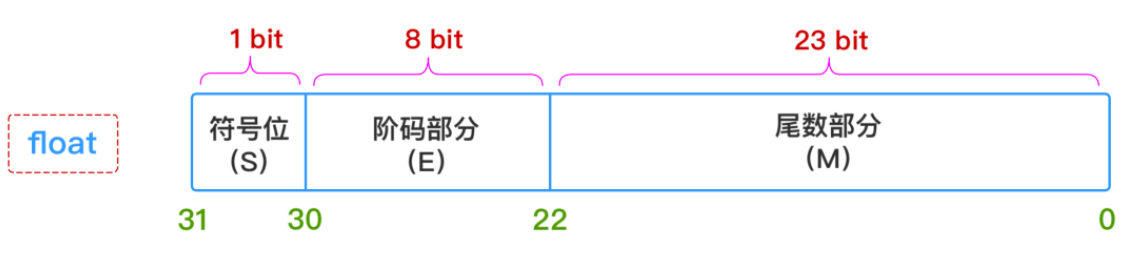
float存储结构
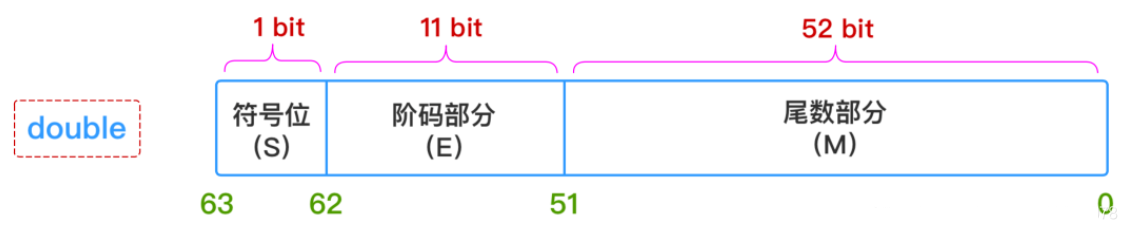
double存储结构
因为指数位影响数的大小，指数位决定大小范围。而小数位则决定计算精度，小数位能表示的数越大，则能计算的精度越大。
float 的小数位只有 23 位，即二进制的 23 位，能表示的最大的十进制数为 2 的 23 次方，即 8388608，即十进制的 7 位，严格点，精度只能百分百保证十进制的 6 位运算。
double 的小数位有 52 位，对应十进制最大值为 4 503 599 627 370 496，这个数有 16 位，所以计算精度只能百分百保证十进制的 15 位运算。

浮点数操作

既然浮点数不能精确表示小数，那么在执行浮点数操作时(算数运算、比较运算等)，要考虑精度丢失可能带来的问题。这里以浮点数比较为例，介绍两个浮点数比较带来的死循环问题。

public void createEndlessLoop() {
    double a = 1.6;
    double b = 0.3;
    double c = a + b;
    double d = 1.9;
    while (c != d) {
        System.out.println("c: " + c + ", d: " + d);
    }
    System.out.print("c == d");
}

执行上述方法，该方法将进入到死循环。浮点数的比较，由于精度丢失问题，其比较结果常常与预期相左。一种基本的思路是引入误差来辅助浮点数比较，但是这种做法仍不能满足某些场景。更多该思路的拓展可以参考链接。

如何避免精度丢失

那么如何避免浮点数的精度丢失问题。其实这个问题没有银弹。要根据不同的业务场景，选择合适的处理方式。如果可以不对浮点数进行运算，则尽量不使用浮点数进行运算。如果必须使用浮点数进行运算，要根据场景，选择合适的处理方式。如浮点数四则运算、比较运算场景，使用BigDecimal。上一个问题的正确处理方式如下：

public void createEndlessLoopWithBigDecimal() {
    BigDecimal a = new BigDecimal("1.6");
    BigDecimal b = new BigDecimal("0.3");
    BigDecimal c = a.add(b);
    BigDecimal d = new BigDecimal("1.9");
    while (c.doubleValue() != d.doubleValue()) {
        System.out.println("c: " + c.doubleValue()  + ", d: " + d.doubleValue());
    }
    System.out.print("c == d");
}

注意，这里并没有使用形如"BigDecimal a = new BigDecimal(1.6);"的方式初始化BigDecimal实例，这是因为浮点数无法精确表示，所以使用BigDecimal(Double)创建的BigDecimal是可能损失了精度，其赋值结果可能和实际有差异。考虑下面的代码，将进入死循环。

public void createEndlessLoopWithBigDecimal() {
    BigDecimal a = new BigDecimal(1.6);
    BigDecimal b = new BigDecimal(0.3);
    BigDecimal c = a.add(b);
    BigDecimal d = new BigDecimal(1.9);
    while (c.doubleValue() != d.doubleValue()) {
        System.out.println("c: " + c.doubleValue()  + ", d: " + d.doubleValue());
    }
    System.out.print("c == d");
}

更多BigDecimal使用上的坑，可参考链接。

参考

https://www.cnblogs.com/fuzongle/p/14986543.html Java浮点数计算精度丢失与解决方案
https://www.cnblogs.com/xujishou/p/7491932.html java中double和float精度丢失问题
https://www.runoob.com/w3cnote/decimal-decimals-are-converted-to-binary-fractions.html 十进制小数转化为二进制小数
https://blog.csdn.net/qq_36915078/article/details/106019023 浮点数如何转二进制
https://www.runoob.com/w3cnote/java-the-different-float-double.html Java 浮点类型 float 和 double 的主要区别
https://www.cnblogs.com/PrimoPrimo/archive/2013/02/22/3307196.html 浮点数的比较
https://blog.csdn.net/wangxufa/article/details/121722126 BigDecimal源码分析及使用

原创不易，如果本文对您有帮助，欢迎关注我，谢谢 ~_~