文章转自:https://www.jb51.net/article/75801.htm
这篇文章主要介绍了解决JavaScript数字精度丢失问题的方法,需要的朋友可以参考下
本文分为三个部分
- JS 数字精度丢失的一些典型问题
- JS 数字精度丢失的原因
- 解决方案(一个对象+一个函数)
一、JS数字精度丢失的一些典型问题
1. 两个简单的浮点数相加
| 1 |
|

这真不是 Firebug 的问题,可以用alert试试 (哈哈开玩笑)。
看看Java的运算结果
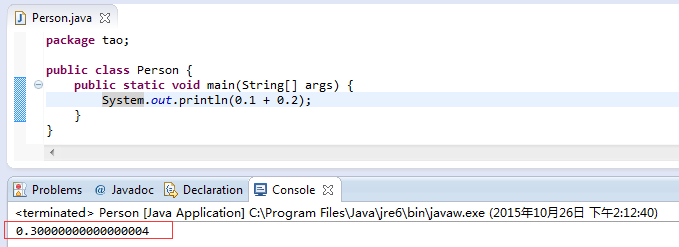
再看看Python

2. 大整数运算
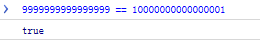
16位和17位数竟然相等,没天理啊。
又如
| 1 2 |
|
看结果

三观又被颠覆了。
3. toFixed 不会四舍五入(Chrome)
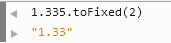
线上曾经发生过 Chrome 中价格和其它浏览器不一致
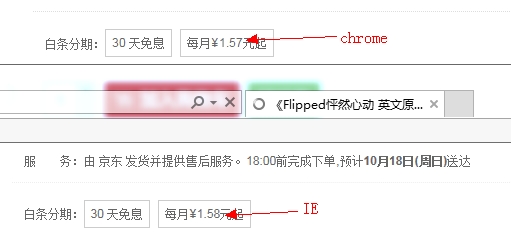
二、JS 数字丢失精度的原因
计算机的二进制实现和位数限制有些数无法有限表示。就像一些无理数不能有限表示,如 圆周率 3.1415926...,1.3333... 等。JS 遵循 IEEE 754 规范,采用双精度存储(double precision),占用 64 bit。如图
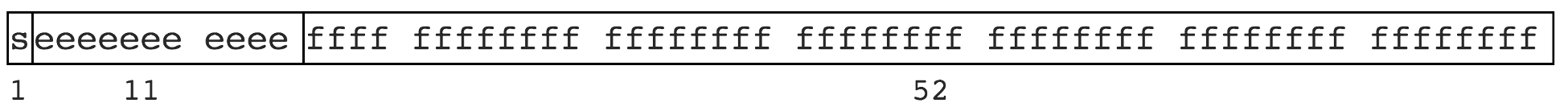
意义
- 1位用来表示符号位
- 11位用来表示指数
- 52位表示尾数
浮点数,比如
| 1 2 |
|
此时只能模仿十进制进行四舍五入了,但是二进制只有 0 和 1 两个,于是变为 0 舍 1 入。这即是计算机中部分浮点数运算时出现误差,丢失精度的根本原因。
大整数的精度丢失和浮点数本质上是一样的,尾数位最大是52位,因此 JS 中能精准表示的最大整数是 Math.pow(2, 53),十进制即 9007199254740992。
大于 9007199254740992 的可能会丢失精度
| 1 2 3 |
|
实际上
| 1 2 3 4 |
|
结果如图
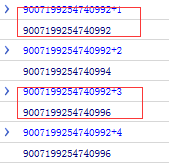
以上,可以知道看似有穷的数字, 在计算机的二进制表示里却是无穷的,由于存储位数限制因此存在“舍去”,精度丢失就发生了。
三、解决方案
对于整数,前端出现问题的几率可能比较低,毕竟很少有业务需要需要用到超大整数,只要运算结果不超过 Math.pow(2, 53) 就不会丢失精度。
对于小数,前端出现问题的几率还是很多的,尤其在一些电商网站涉及到金额等数据。解决方式:把小数放到位整数(乘倍数),再缩小回原来倍数(除倍数)
| 1 2 |
|
以下是我写了一个对象,对小数的加减乘除运算丢失精度做了屏蔽。当然转换后的整数依然不能超过 9007199254740992。
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
|
toFixed的修复如下
| 1 2 3 4 5 6 7 |
|
以上就是关于JavaScript数字精度丢失问题全部内容,对典型问题进行分析,分析数字精度丢失原因,还分享了解决方案,希望对大家的学习有所帮助。
最后
以上就是陶醉帆布鞋最近收集整理的关于解决JavaScript数字精度丢失问题的方法的全部内容,更多相关解决JavaScript数字精度丢失问题内容请搜索靠谱客的其他文章。








发表评论 取消回复