概述
一、算法设计：将两个递增的有序链表合并为一个递增的有序链表。要求结果链表仍使用原来两个链表的存储空间，不另外占用其它的存储空间。表中不允许有重复的数据。
第一题的解法其实很简单，首先利用指针改变指向的空间地址从而达到排序。如图，有两个递增的有序链表La和Lb，用两个指针p1和p2分别指向La->next和Lb->next，这样可以读取到有序链表之后的数据，在利用两个有序链表的第一个数据比较得到虚拟头指针d应该指向哪个有序链表的头指针是La还是Lb。这样就能确定接下来需要排序的头指针了。
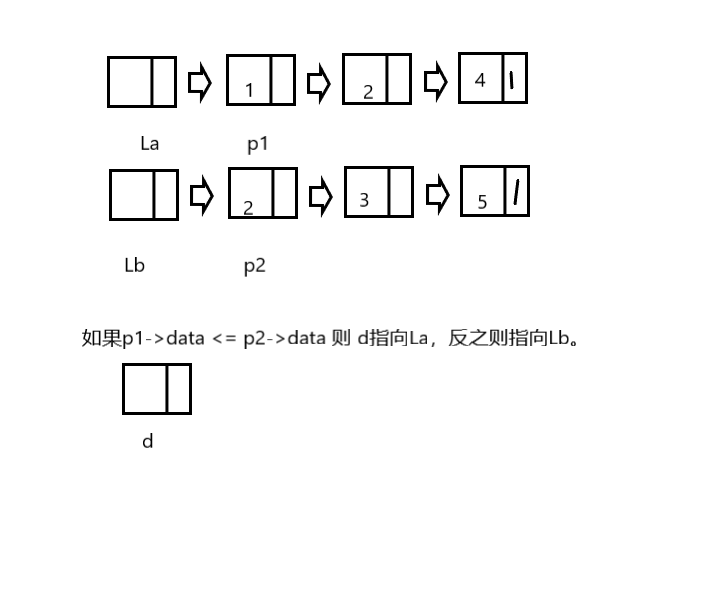
第二步，虚拟指针v指向p1和p2比较后指向最小的数据的那个指针，然后最小数据的那个指针向后移动，这样方便之后的比较，以后比较出来最小的那个让虚拟指针v->next 指向那个最小的数据的指针所指向的空间。大致思路是这样代码如下:
LinkList CompareList(LinkList La,LinkList Lb){
LinkList p1,p2,d,v;
p1 = La->next;
p2 = Lb->next;
if(p1->data <= p2->data){
d = La;
}
else{
d = Lb;
}
v = d;
while(p1 != NULL && p2 != NULL ){
if(p1->data < p2->data){
v->next = p1;
p1 = p1->next;
v = v->next;
}
else if(p1->data > p2->data){
v->next = p2;
p2 = p2->next;
v = v->next;
}
else if(p1->data == p2->data){
v->next = p1;
p1 = p1->next;
v = v->next;
v->next = p2;
p2 = p2->next;
v = v->next;
}
}
if(p1 != NULL) v->next = p1;
else if(p2 != NULL) v->next = p2;
return d;
}
二、算法设计：将两个非递减的有序链表合并为一个非递增的有序链表。要求结果链表仍使用原来两个链表的存储空间，不另外占用其它的存储空间。表中允许有重复的数据。
这道题的思路和刚才那道题思路差不多，只不过刚才那道题利用的是链表的后插法，这道题利用后插法。
首先先确定虚拟头指针的指向，因为这道题是两个递增的有序链表合并成一个递减的有序链表那么先找到最小的插进去，用前插法插入这样最后插入到虚拟头指针的那个数便是最大的，这样就合并成了一个递减有序链表。
代码如下:
LinkList CompareList(LinkList &La,LinkList &Lb){
LinkList d,v,p1,p2;
p1 = La->next;
p2 = Lb->next;
if(p1->data <= p2->data){
d = La;
v = p1;
p1 = p1->next;
v->next = NULL;
}
else {
d = Lb;
v = p2;
p2 = p2->next;
v->next = NULL;
}
while(p1 != NULL && p2 != NULL){
if(p1->data < p2->data){
v = p1;
p1 = p1->next;
v->next = d->next;
d->next = v;
}
else if(p1->data > p2->data){
v = p2;
p2 = p2->next;
v->next = d->next;
d->next = v;
}
else {
v = p1;
p1 = p1->next;
v->next = d->next;
d->next = v;
v = p2;
p2 = p2->next;
v->next = d->next;
d->next = v;
}
}
while(p1 != NULL){
v = p1;
p1 = p1->next;
v->next = d->next;
d->next = v;
}
while(p2 != NULL){
v = p2;
p2 = p2->next;
v->next = d->next;
d->next = v;
}
return d;
}
三、算法设计：设计一个算法，删除递增有序涟表中值大于mink且小于ma×k的所有元素(mink和maxk是给定的两个参数，其值可以和表中的元素相同，也可以不同）。
这道题和前两道题的思路不一样，但是很好想，因为你删除的是一个表的一段区域，那么首先最重要的就是确定这段区域的头在哪里，由于是递增有序链表那么先找到和mink相同的值的那个空间的下一个空间地址就是这段区域的头，从这个头开始依次删除这些空间直到maxk这个值的空间截止，然后再将剩下的两段区域接上。这是其中一种情况，还有两种情况，一种是mink的值大于这个递增有序链表的任何一个值，不需要删除。另一种情况是maxk大于这个递增有序链表中的任何一个值，但是mink确存在这个表中。需要删掉mink值后的一整段。
代码如下:
LinkList DeleteList(LinkList &L,int mink,int maxk){
LinkList p,v,q,n;
p = L->next;
v = L;
while(p->data != mink){
v = p;
p = p->next;
if(p->next == NULL) return L;
}
q = p;
p = p->next;
v = p;
while(p->data != maxk){
n = p;
p = p->next;
if(p->next == NULL) {
q->next = NULL;
while(v->next != NULL){
n = v;
v = v->next;
delete n;
}
return L;
}
}
q->next = p;
n->next = NULL;
while(v->next != NULL){
n = v;
v = v->next;
delete n;
}
return L;
}
四、算法设计：已知长度为n的线性表A采用顺序存储结构，请写一时间复杂度为0（n）、空间复杂度为O（1）的算法，该算法删除线性表中所有值为item的数据元素。
弄懂上面三种算法写这道题就会简单很多因为这道题也是利用了相同的道理，只不过这道题是将这个线性表每判定一次就重新填入数据。
代码如下:
void Delete(List &L,int item){
int i,j,countL;
i = 0;
j = 0;
countL = 0;
for(i=0; i<L.length;){
if(L.d[i] == item){
i++;
countL++;
}
else{
L.d[j] = L.d[i];
i++;
j++;
}
}
L.length -= countL;
}
最后
以上就是魔幻砖头为你收集整理的关于算法设计的一种思路的全部内容，希望文章能够帮你解决关于算法设计的一种思路所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复