传统算法-知识总结-递推+递归+分治+动态规划+贪心算法+回溯算法+分支
目录
一:算法基础
1.1.算法基础介绍
1.1.1 算法满足4条性质:
1.1.2 算法定义:
1.1.3 算法设计过程
1.2.欧几里德算法介绍
1.2.1 定义:
1.2.2 算法内容:
1.2.3 算法证明:
二.递推
2.1 递推的定义
2.2 迭代法求解递推方程
2.3 递推样例
2.3.1 一元多项式求导
2.3.2分鱼程序
三:递归
3.1 递归:
3.2 实例:
3.2.1 阶乘
3.2.2 Fibonacci数列:
3.3 经典hanoi塔问题
3.3.1 问题定义:
3.3.2 解题思路
3.3.3Java代码实现hanoi塔
四:分治
4.1 分治的基本概念
4.1.1.基本介绍
4.1.2 算法的一般设计模式
4.2 二分搜索技术
4.2.1 Java中封装的二分搜索
4.2.2二分搜索描述和思想
4.2.3 代码实现:
4.3 快速排序
4.3.1 快排的定义和思想:
4.3.2 图解快排过程
4.3.3 代码实现
五:贪心算法
5.1 贪心算法基本概念
5.1.1 定义
5.1.2 贪心算法的基本思路
5.1.3 贪心算法适用问题
5.2 背包问题
六:动态规划
6.1 动态规划引例-钞票使用问题
6.1.1 问题描述
6.1.2 如何避免不是最优解
6.1.3 钞票问题代码
6.2 基本概念:
6.2.1 动态规划的定义:
6.2.2 无后效性
6.2.3 最优子结构
6.3 动态规划样例:最长公共子系列
6.3.1 最长子问题描述:
6.3.2 最长子问题分析
6.3.3 最长子问题解决
七:回溯法
7.1 回溯法的基本定义和思想
7.2 回溯法的解题步骤
7.3 回溯法代码框架
7.3.1 递归回溯框架
7.3.2 非递归的算法框架
7.4 n皇后问题
7.4.1 题目描述
74.2.代码实现
八:分支限界
8.1.基本介绍
8.2 分支限界法与回溯法的区别
8.3 分支限界--单源最短路径问题
8.3.1 单源最短路径问题介绍
8.3.2 单源最短路径问题思路
8.3.3 单源最短路径问题代码实现
九.参考文献
一:算法基础
1.1.算法基础介绍
1.1.1 算法满足4条性质:
1)输入:有0个或者多个由外部提供的的量作为算法的输入
2)输出:算法产生至少一个量作为输出
3)确定性:组成算法的每条指令是清晰的和无歧义的
4)有限性:算法中每条指令的执行次数是有限的,执行每条指令的时间也是有限的。
1.1.2 算法定义:

1.1.3 算法设计过程


1.2.欧几里德算法介绍
1.2.1 定义:
欧几里德算法也被称为辗转相除法,用于计算两个整数a, b的最大公因子。符号记为:gcd(a,b).特别gcd(0, n) = 0,因为任何整数都能整除0;
1.2.2 算法内容:

通俗的讲:假设a比b大,我们要找a, b的最大公因子。第一步,用a除以b余数为y.第二步:把第一步中的除数当作被除数,把第一步中的余数当作除数再进行相除;第三步:重复第二步的步骤,一直到余数为0,结束算法,此时剩余的最后的被除数就是我们要找的最大公因子。
1.2.3 算法证明:
对于任何可以整除a和b的整数,那么它也一定可以整除(a-b)和 b.选择该整数为gcd(a, b);同理,任何可以整除a-b和b的整数,一定可以整除a和b,因此我们选择该整数为gcd(a-b,b);由此可得:gcd(a,b)=gcd(a-b,b)。
因为总有整数n,使得 a - n*b = a mod b,所以迭代可知:gcd(a-b,b)=gcd(a-2b,b)=...=gcd(a-n*b,b)=gcd(a mod b,b)。
二.递推
2.1 递推的定义
一个问题的求解需一系列的计算,在已知条件和所求问题之间总存在着某种相互联系的关系,在计算时,如果可以找到前后过程之间的数量关系(即递推式),那么,从问题出发逐步推到已知条件,此种方法叫逆推。无论顺推还是逆推,其关键是要找到递推式。
递推算法的首要问题是得到相邻的数据项间的关系(即递推关系)。递推算法避开了求通项公式的麻烦,把一个复杂的问题的求解,分解成了连续的若干步简单运算。一般说来,可以将递推算法看成是一种特殊的迭代算法
2.2 迭代法求解递推方程
不断用递推方程的右部替换左部,每次替换,随着 n 的降低在和式中多出一项,直到出现初值停止迭代,将初值代入并对和式求和
可用数学归纳法验证解的正确性
2.3 递推样例
2.3.1 一元多项式求导
(1)题目

(2)c语言求解

(3)Java语言求解
注意四个细节
- 第一个坑:数字之间可能有多个空格 如果你是用Java切割字符串的话
- 第二个坑:当系数项是0的时候输出0 0 *如:3 4 -5 2 6 1 0 1 对应输出是12 3 -10 1 6 0 0 但是题目给出的输出是 12 3 -10 1 6 0
- 第三个坑:当系数项不是0,指数是0的时候 什么也不输出 *如:3 4 -5 2 6 1 -2 0 对应输出是12 3 -10 1 6 0 (-2 0没对应的数字输出)
- 第四个坑:当输出多项式是空串的时候要输出0 0 *如:输入只有 -2 0 的时候 输出空串 但是此时必须输出0 0
代码实现:
package temp;
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String arg[]) {
System.out.println("请输入整数: ");
int n,fac;
Scanner scan = new Scanner(System.in);
String str = scan.nextLine();
String[] newstr =str.split("\s+");
ArrayList<Integer>alist = new ArrayList<Integer>();
for(int i=0;i<newstr.length;i=i+2) {
int j = i+1;
if(Integer.valueOf(newstr[i])==0){
alist.add(0);
alist.add(0);
}
if(Integer.valueOf(newstr[i])!=0&&Integer.valueOf(newstr[j])==0) {
}
if(Integer.valueOf(newstr[i])!=0&&Integer.valueOf(newstr[j])!=0) {
alist.add(Integer.valueOf(newstr[i])* Integer.valueOf(newstr[j]));
alist.add(Integer.valueOf(newstr[j])-1);
}
}
if(alist.isEmpty()){ //如果将要输出的是空字符串,那么就输出0 0
System.out.println("0 0");
}else{
for(int i=0 ;i<alist.size() ;i++){
System.out.print(alist.get(i));
if(i!=alist.size()-1){
System.out.print(" "); //行末不能有空格 控制空格的输出
}
}
}
System.out.println();
}
}
2.3.2分鱼程序
题目:
A、B、C、D、E五个人在某天夜里合伙去捕鱼,到第二天凌晨时都疲惫不堪,于是各自找地方睡觉。日上三杆,A第一个醒来,他将鱼分为五份,把多余的一条鱼扔掉,拿走自己的一份。B第二个醒来,也将鱼分为五份,把多余的一条鱼扔掉,保持走自己的一份。C、D、E依次醒来,也按同样的方法拿走鱼。问他们合伙至少捕了多少条鱼?
这个程序非常巧妙,先给a[0]一个初值为6,然后利用6去计算其他的鱼,在进行判断比较。
package temp;
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String arg[]) {
int countsum = 6;
for(int i=6; ;i++)
{
int count2 =(i-1)/5*4;
int count3 = (count2-1)/5*4;
int count4 = (count3-1)/5*4;
int count5 = (count4-1)/5*4;
if(i%5==1&&count2%5==1&&count3%5==1&&count4%5==1&&count5%5==1) {
System.out.println(i);
break;
}
}
}
}
三:递归
3.1 递归:
直接或者间接地调用自身的算法成为递归算法。用函数自身给出定义的函数称为递归函数。
3.2 实例:
3.2.1 阶乘
(1)阶乘函数可递归定义为:
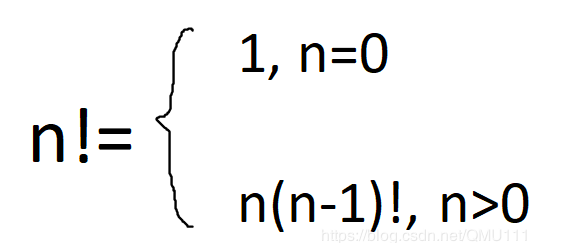
(2)代码实现
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String arg[]) {
System.out.println("请输入整数: ");
int n,fac;
Scanner scan = new Scanner(System.in);
n= scan.nextInt();
//int []Result_Seq=new int[n];
fac = factorial(n);
System.out.println(fac);
}
public static int factorial(int m) {
if(m==0) return 1;
else return m*factorial(m-1);
}
}
3.2.2 Fibonacci数列:
(1)定义:
无穷数列1,1,2,3,5,8,13,21,34,55,........,称为Fibonacci数列,表现形式:
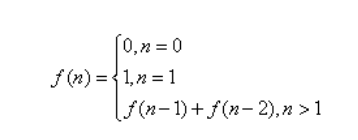
(2)代码实现
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String arg[]) {
System.out.println("请输入整数: ");
int n,fac;
Scanner scan = new Scanner(System.in);
n= scan.nextInt();
//int []Result_Seq=new int[n];
fac = fibonacci(n);
System.out.println(fac);
}
public static int fibonacci(int m) {
if(m<=1) return 1;
else return fibonacci(m-1)+fibonacci(m-2);
}
}
3.3 经典hanoi塔问题
3.3.1 问题定义:
汉诺塔是根据一个传说形成的一个问题。汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着 64 片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
我们将 Hanoi 问题抽象为一种数学问题。首先给出如下三个柱子 A、B、C,其中 A 柱子上有从上到下从小叠到大的 N 个云盘。现要求将A柱子上的圆盘都移动到 C 柱子上,其中,每次移动都必须满足:
每次只能移动一个圆盘
小圆盘上不能放大圆盘
那么针对这个数学问题,就可以提出相关问题:
移动 N 个圆盘最少需要多少次
第 M 步移动的是哪个圆盘以及圆盘移动方向
解题:设总共有 N 个圆盘,Steps表示总移动次数
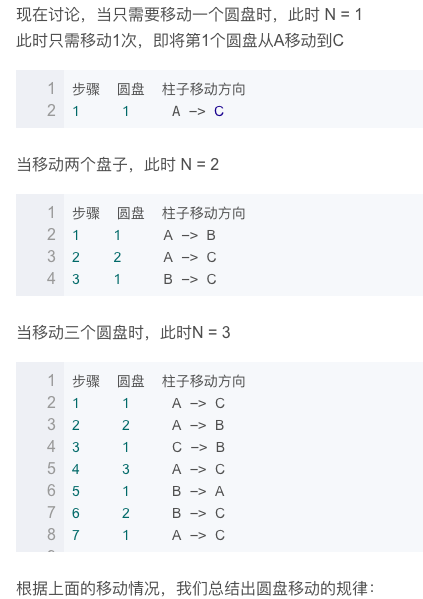
3.3.2 解题思路

3.3.3Java代码实现hanoi塔
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
static long s = 0;
public static void main(String args[]) {
System.out.println("开始hanoi塔游戏 ");
int n = 0;
Scanner console = new Scanner(System.in);
n = console.nextInt();
System.out.println("汉诺塔层数为" + n);
System.out.println("移动方案为:");
hanoi(n, 'a', 'b', 'c');
System.out.println("需要移动次数:" + s);
}
static void hanoi(int n, char a, char b, char c) { //a为初始塔,b为目标塔,c为辅助塔
if (n == 1){
System.out.println("n=" + n + " " + a + "-->" + c);
s++;
}
else{
/*递归的调用*/
hanoi(n-1,a,b,c); // 把 a移动到c借助b;
System.out.println("n=" + n + " " + a + "-->" + c);
hanoi(n-1,b,a,c); //把b 移动到a借助c.
s++;
}
}
}
四:分治
4.1 分治的基本概念
4.1.1.基本介绍
分治法的基本思想是将一个规模为n的问题分解为k个规模较小的子问题,这些子问题互相独立且与原问题相同。递归地解决这些子问题,然后将各个子问题的解合并得到原问题的解。
4.1.2 算法的一般设计模式
divide-and-conquer(P){
if(|P| <= n0){
divide P into smaller subinstances P1, P2,.....,Pk;
for(i = 1; i<= k; i++){
yi = divide-and-conquer(Pi);
}
return merge(y1 , y2, ....., yk);
}
}从分治算法的一般设计模式可以看出,用它设计出的程序一般是递归算法。
4.2 二分搜索技术
4.2.1 Java中封装的二分搜索
以Java为例,二分搜索已经被封装了,例如,我们写代码的时候可以直接使用语句:
int pos = currentItemset.binarySearch(item); binarySearch()方法,若搜索键包含在列表中,则返回键的索引,否则,返回-1;
4.2.2二分搜索描述和思想
(1)问题描述:
给定已经排好序的n个元素a[ 0 : n-1],现在要在这n个元素中找出一特定元素x.
(2)核心思想:
二分搜索方法的基本思想是将n个元素分成个数大致相同的的两半,取a[n / 2]与x作比较,如果x = a[n / 2],说明找到x,算法终止。如果x < a[n / 2],则只需要在数组a的左半部分继续搜索x; 如果x > a[n / 2],则只需要在a的右半部分继续搜索x.
4.2.3 代码实现:
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String args[]) {
System.out.println("请输入一行从小到大排序好的整数: ");
Scanner scan = new Scanner(System.in);
String str = scan.nextLine();
System.out.println("请输入要寻找的数 ");
int x =scan.nextInt();
String[] newstr = str.split("\s+");
ArrayList<Integer> a = new ArrayList<Integer>();
for(int i=0; i<newstr.length; i++) {
if(Integer.valueOf(newstr[i]) != ' ') {
a.add(Integer.valueOf(newstr[i]));
}
}
//System.out.println(x);
int start = 0;
int end = a.size();
int flag = binarysearch(a,x,start,end);
if(flag == 1) {
System.out.println("搜索成功");
}else {
System.out.println("搜索失败");
}
}
static int binarysearch(ArrayList<Integer> a, int x,int start, int end) {
int flag = 0;
while(start<= end) {
int middle = (start+end)/2;
if(a.indexOf(middle) == x) {
flag =1;
System.out.println("找到了:" + a.indexOf(middle));
break;
}
else if(x< a.indexOf(middle)) {
end = middle -1;
binarysearch(a, x, start, end);
}
else if(x > a.indexOf(middle)) {
start = middle+1;
binarysearch(a,x,start,end);
}
}
return flag;
}
}
4.3 快速排序
4.3.1 快排的定义和思想:
快速排序算法是基于分治策略的一个排序算法。
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个 10 个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便,就让第一个数 6 作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在 6 的右边,比基准数小的数放在 6 的左边,类似下面这种排列。 3 1 2 5 4 6 9 7 10 8
核心思想步骤为:分解->递归->合并
4.3.2 图解快排过程
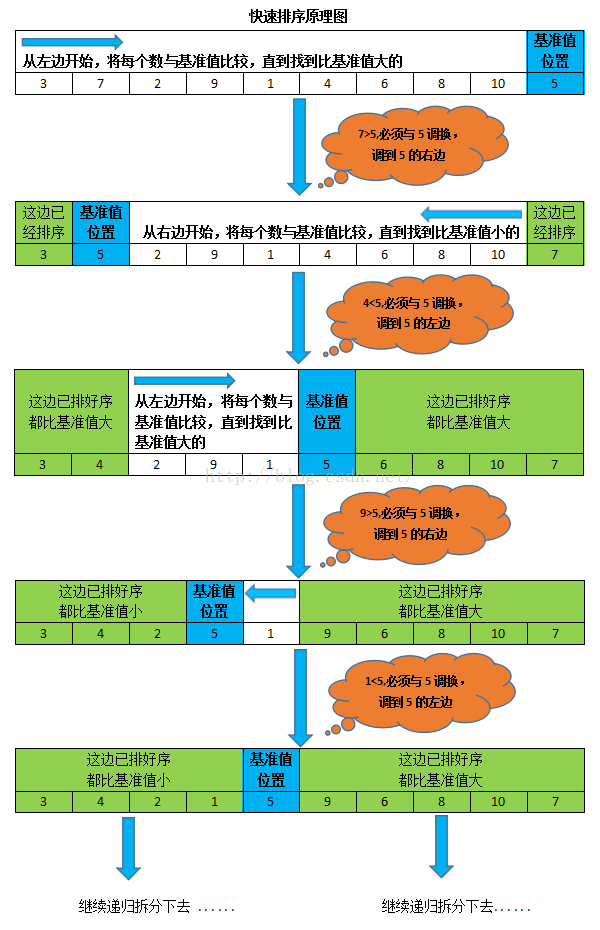
4.3.3 代码实现
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String args[]) {
int[] a = new int[]{2,7,4,5,10,1,9,3,8,6};
int[] b = new int[]{1,2,3,4,5,6,7,8,9,10};
int[] c = new int[]{10,9,8,7,6,5,4,3,2,1};
int[] d = new int[]{1,10,2,9,3,2,4,7,5,6};
sort(a, 0, a.length-1);
System.out.println("排序后的结果:");
for(int x : a){
System.out.print(x+" ");
}
}
public static int divide(int a[],int start , int end) {
int base = a[end]; //每次以最右边的元素为基准值
while(start < end) {
while(start < end && a[start] <= base)
//从左边开始遍历,如果目前值比基准值小,就继续往右走
start++;
if(start < end) {
int temp = a[start];
a[start] = a[end];
a[end] = temp;
end--; // 交换后,此时那个被调换的值也同时调到了正确的位置()
}
while(start < end && a[end] >= base)
end--; // 从右边开始遍历
if(start < end) {
int temp = a[start];
a[start] = a[end];
a[end] = temp;
start++;
}
}
return end; //return start 也行
}
public static void sort (int[] a , int start , int end) {
if(start > end ) {
return ; // 如果只有一个元素,则不需要排序
}
else {
int partition = divide(a,start,end);
sort(a, start , partition-1);
sort(a, partition+1, end);
}
}
}
五:贪心算法
5.1 贪心算法基本概念
5.1.1 定义
在问题求解时,总是做出当前看来是最好的选择。也就是说不从整体最
优上加以考虑,所做出的仅仅是某种意义上的局部最优解。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
5.1.2 贪心算法的基本思路
(1)建立数学模型描述问题;
(2)把求解的问题分解成若干子问题;
(3)对每一个子问题求解,得到子问题的局部最优解;
(4)把子问题的局部最优解合成原来解问题的一个解
5.1.3 贪心算法适用问题
贪心策略适用的前提就是局部最优解能够产生全局最优解。一般,对一个问题分析是否适用于贪心算法,可以先选择该问题下的几个实际数据进行分析,就可做出判断
5.2 背包问题
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String[] args) {
// 单位重量价值分别为:10 5 7 6 3 8 90 100
double w[] = { 0, 50, 80, 30, 40, 20, 60, 10 ,1};//物体的重量
double v[] = { 0, 500, 400, 210, 240, 60, 480, 900,100 };//物体的价值
double M = 170;// 背包所能容纳的重量
int n = w.length - 1;// 物体的个数
double[] x = new double[n + 1];// 每个物体装进的比例,大于等于0并且小于等于1
packages(w, v, M, n, x);//调用贪心算法函数
System.out.println("排序后的物体的重量:");
for(int i=1;i<=n;i++){
System.out.print(w[i]+"t");
}
System.out.println();
System.out.println("排序后的物体的价值:");
for(int i=1;i<=n;i++){
System.out.print(v[i]+"t");
}
double[]t=new double[n+1];//定义一个数组表示单位重量物体的价值
for(int i=1;i<=n;i++){
t[i]=v[i]/w[i];
}
//用冒泡排序对double[]t进行排序(大的在前)
for(int i=1;i<=n;i++){
for(int j=1;j<=n-i;j++){
if(t[j]<t[j+1]){
double temp=t[j];
t[j]=t[j+1];
t[j+1]=temp;
}
}
}
System.out.println();
System.out.println("排好序后的单位物体的价值: ");
for(int i=1;i<=n;i++){
System.out.print(t[i]+"t");
}
double maxValueSum=0; //用来存放背包能装下的物体的最大价值总和
for(int i=1;i<x.length;i++){
maxValueSum+=x[i]*v[i];
}
System.out.println();
System.out.println("排序后每个物体装进背包的比例:");
for(int i=1;i<=n;i++){
System.out.print(x[i]+"t");
}
System.out.println();
System.out.println("背包能装下的物体的最大价值总和为: "+maxValueSum);
}
public static void packages(double[] w, double[] v, double M, int n, double[] present) {
unitvaluesort(w,v,n);
double restcapacity = M ; // 背包剩余的容量
int i; //表示第几个物品
for(i = 1; i<= n; i++) {
if(w[i] <= restcapacity) {
present[i] =1;
restcapacity = restcapacity - w[i];
}
else {
break;
}
}
if(i<= n) {
present[i] = restcapacity/w[i];
}
}
public static void unitvaluesort(double[] w, double[] v, int n) {
double[] unitvalue = new double[n+1];
for(int i=1;i<=n;i++) {
unitvalue[i] = v[i]/w[i];
}
// 以单位重量的价值的大小进行排序,同时以此为依据
for(int i =1; i<= n; i++) {
for(int j=1; j<=n-1; j++) {
if(unitvalue[j]< unitvalue[j+1]) {
double temp = unitvalue[j];
unitvalue[j] = unitvalue[j+1];
unitvalue[j+1] = temp;
double temp2=w[j];
w[j]=w[j+1];
w[j+1]=temp2;
double temp3=v[j];
v[j]=v[j+1];
v[j+1]=temp3;
}
}
}
}
}
5.3 哈夫曼编码
5.4 单源最短路径之dijkstra
5.5 最小生成树之prim
5.6 最小生成树之kruskal
(5.3节到5.6节暂时不写博客,后期有空闲时间再补上)
六:动态规划
6.1 动态规划引例-钞票使用问题
6.1.1 问题描述
假设您是个土豪,身上带了足够的1、5、10、20、50、100元面值的钞票。现在您的目标是凑出某个金额w,需要用到尽量少的钞票。依据生活经验,我们显然可以采取这样的策略:能用100的就尽量用100的,否则尽量用50的……依次类推。在这种策略下,666=6×100+1×50+1×10+1×5+1×1,共使用了10张钞票。这种策略称为“贪心”:假设我们面对的局面是“需要凑出w”,贪心策略会尽快让w变得更小。能让w少100就尽量让它少100,这样我们接下来面对的局面就是凑出w-100。长期的生活经验表明,贪心策略是正确的。但是,如果我们换一组钞票的面值,贪心策略就也许不成立了。如果一个奇葩国家的钞票面额分别是1、5、11,那么我们在凑出15的时候,贪心策略会出错:
15=1×11+4×1 (贪心策略使用了5张钞票)
15=3×5 (正确的策略,只用3张钞票)
为什么会这样呢?贪心策略错在了哪里?鼠目寸光。
刚刚已经说过,贪心策略的纲领是:“尽量使接下来面对的w更小”。这样,贪心策略在w=15的局面时,会优先使用11来把w降到4;但是在这个问题中,凑出4的代价是很高的,必须使用4×1。如果使用了5,w会降为10,虽然没有4那么小,但是凑出10只需要两张5元。在这里我们发现,贪心是一种只考虑眼前情况的策略。
6.1.2 如何避免不是最优解
如果直接暴力枚举凑出w的方案,明显复杂度过高。太多种方法可以凑出w了,枚举它们的时间是不可承受的。我们现在来尝试找一下性质。重新分析刚刚的例子。w=15时,我们如果取11,接下来就面对w=4的情况;如果取5,则接下来面对w=10的情况。我们发现这些问题都有相同的形式:“给定w,凑出w所用的最少钞票是多少张?”接下来,我们用f(n)来表示“凑出n所需的最少钞票数量”。那么,如果我们取了11,最后的代价(用掉的钞票总数)是多少呢?明显cost =f(4)+1=4+1=5 ,它的意义是:利用11来凑出15,付出的代价等于f(4)加上自己这一张钞票。现在我们暂时不管f(4)怎么求出来。
依次类推,马上可以知道:如果我们用5来凑出15,cost就是 f(10)+1 = 2+1 =3。
那么,现在w=15的时候,我们该取那种钞票呢?当然是各种方案中,cost值最低的那一个!
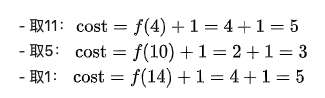

这个式子是非常激动人心的。我们要求出f(n),只需要求出几个更小的f值;既然如此,我们从小到大把所有的f(i)求出来不就好了?注意一下边界情况即可。
6.1.3 钞票问题代码
import java.util.ArrayList;
import java.util.Scanner;
public class algorithmtest001 {
public static void main(String[] args) {
int n=15;
int[] f = new int[16];
f[0] = 0;
for(int i=1; i<= n; i++) {
int cost = 100;
if(i>=11) {
cost = Math.min(cost , f[i-11]+1);
}
if(i>=5) {
cost = Math.min(cost , f[i-5]+1);
}
if(i>=1) {
cost = Math.min(cost , f[i-1]+1);
}
f[i]= cost;
System.out.println("请输出此时的整数n对应的次数:: "+ i+ " : "+cost);
}
}
}
运行结果:

6.2 基本概念:
6.2.1 动态规划的定义:
动态规划与分治法类似,其基本思想也是将待求问题分解成若干子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合与用动态规划求解的问题,经分解得到的子问题往往不是互相独立的,若使用分治法来解决这类问题,则分解得到的子问题数目太多,以至于最后解决原问题需要耗费指数时间,然而,不同子问题的数目常常只有多项式量级。在用分治法求解时,有些子问题被重复计算了许多次。如果能够保存已经解决子问题的答案,在需要的时候再找出这些已经求得的答案,这样就可以避免大量的重复运算,从而得到多项式时间算法。
为了达到上述目的,可以使用一个表来记录所有已经解决子问题的答案。不管子问题以后是否被用到,只要它被计算过,就将结果填入表中。这就是动态规划的基本思想。
6.2.2 无后效性
如果给定某一阶段的状态,则在这一阶段以后过程的发展不受这阶段以前各段状态的影响。即未来与过去无关。例如,
一旦f(n)确定,“我们如何凑出f(n)”就再也用不着了。要求出f(15),只需要知道f(14),f(10),f(4)的值,而f(14),f(10),f(4)是如何算出来的,对之后的问题没有影响。
6.2.3 最优子结构
回顾我们对f(n)的定义:我们记“凑出n所需的最少钞票数量”为f(n)。f(n)的定义就已经蕴含了“最优”。利用w=14,10,4的最优解,我们即可算出w=15的最优
大问题最优解可以由小问题的最优解推出。
6.3 动态规划样例:最长公共子系列
6.3.1 最长子问题描述:
LCS问题陈述:给定两个序列,找出两个序列中存在的最长子序列的长度。子序列是以相同的相对顺序出现的序列,但不一定是连续的。例如,“abc”、“abg”、“bdf”、“aeg”、“'”acefg“等等都是“abcdefg”的子序列。所以一个长度为n的字符串有2^n个不同的可能子序列。具体例子:对于给定的字符串 “ABCDGH” 和 “AEDFHR”,其最长公共子序列为: “ADH”,最长公共子序列的长度为:3。对于给定的字符串 “AGGTAB” 和 “GXTXAYB”,其最长公共子序列为:“GTAB”,最长公共子序列的长度为:4。
6.3.2 最长子问题分析

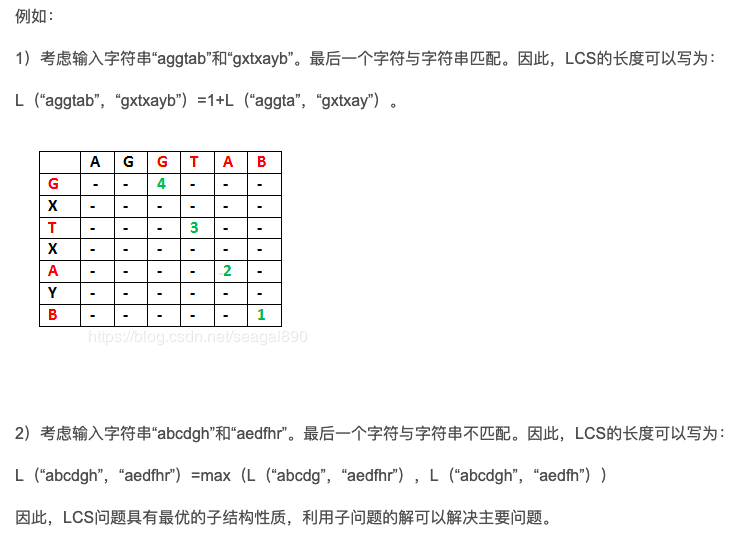
6.3.3 最长子问题解决
由上面的分析可以看到,问题具有递归结构。因此可以使用递归算法。但是因为该问题具有重叠子结构性质,为了避免有些子问题中同一个子问题被重复计算,我们使用动态规划算法实现。
代码实现
import java.util.ArrayList;
import java.util.Scanner;
public class temp {
public static void main(String[] args) {
//algorithmtest001 lcs = new algorithmtest001();
String s1 = "AGGTAB";
String s2 = "GXTXAYB";
char[] X = s1.toCharArray();
char[] Y = s2.toCharArray();
int m = X.length;
int n = Y.length;
System.out.println("Length of LCS is "+ " "+ lcs(X,Y,m,n));
}
static int lcs(char[] X, char[] Y, int m, int n) {
int L[][] = new int[m+1][n+1];
for(int i=0; i<= m; i++) {
for(int j=0; j<= n; j++) {
if(i == 0 || j==0) {
L[i][j] = 0;
}
else if(X[i -1] == Y[j-1]) {
L[i][j] = L[i-1][j-1] +1;
}
else {
L[i][j] = Math.max(L[i-1][j], L[i][j-1]);
}
}
}
return L[m][n];
}
}
七:回溯法
7.1 回溯法的基本定义和思想
回溯法有“通用的解题法”之称。用回溯法可以系统地搜索一个问题的所有解或者任意解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。它在问题的解空间树中按照深度优先策略,从根结点出发搜索解空间树。算法搜索至解空间树的任一节点时候,先判断该节点是否包含问题的解。如果肯定不包含,则跳过对以该节点为跟的子树的搜索,逐层向其祖先节点回溯。否则进入该子树,继续按照深度优先策略搜索。回溯法求解问题所有解时,只要搜索到问题的一个解就可以结束。
7.2 回溯法的解题步骤
(1)针对所给问题,确定问题的解空间;(首先明确定义问题的解空间,问题的解空间至少包括包含问题的一个解);
(2)确定节点扩展搜索规则;
(3)以深度优先搜索方式搜索解空间,并且在搜索过程中使用剪枝函数避免无效搜索
7.3 回溯法代码框架
7.3.1 递归回溯框架
回溯法是对解空间的深度优先搜索,在一般情况下使用递归函数来实现回溯法比较简单,其中i为搜索的深度,框架如下f
void backtrack (int t) //t表示递归深度
{
if (t>n) output(x); //n表示深度界限
else
for (int i=f(n,t);i<=g(n,t);i++) // f(n,t),g(n,t)分别表示当前扩展结点未搜索过的子树的起始编号和终止编号
{
x[t]=h(i);
if (constraint(t)&&bound(t)) //满足约束函数和限界函数
backtrack(t+1);
}
}
7.3.2 非递归的算法框架
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if (f(n,t)<=g(n,t))
for (int i=f(n,t);i<=g(n,t);i++) {
x[t]=h(i);
if (constraint(t)&&bound(t)) {
if (solution(t)) output(x);
else t++;}
}
else t--;
}
}
7.4 n皇后问题
7.4.1 题目描述
在n ~n格的棋盘上放置彼此不受攻击的n个皇后按照国际象棋的规则,皇后可以攻击与之处在同一行或者同一列或者同一斜线上的棋子。n皇后问题等价于在n ~n格的棋盘上放置n个皇后,任何两个皇后不放在同一行或者同一列或者同一斜线上。
74.2.代码实现
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;
public class QueenSolution {
private int[][] board = new int[8][8];
private int total = 0; //结果的数量
public void putQueen(int k) {
int max = board.length;
//放置最后一个的时候,说明棋盘放置完毕,输出结果
if(k>= max) {
total++;
System.out.println(String.format("==========%s=======", total));
for(int i =0; i< max;i++) {
System.out.println(Arrays.toString(board[i]));
}
System.out.println("==================");
}
else {
for(int i =0; i< max; i++) {
if(check(k,i)) {
board[k][i] =1;
putQueen(k+1);
board[k][i] = 0;
}
}
}
}
private boolean check(int row, int col) {
// 检查列是否有皇后
for(int i =0; i< row; i++) {
if(board[i][col] == 1) {
return false;
}
}
//检查左上对角线
for(int m = row-1, n= col-1;m>=0&& n>=0;m--,n--) {
if(board[m][n] == 1) {
return false;
}
}
//检查右上对角线是否有皇后
for (int m = row - 1, n = col + 1; m >= 0 && n < board[0].length; m--, n++) {
if (board[m][n] == 1) {
return false;
}
}
return true;
}
public static void main(String[] args) {
QueenSolution solution = new QueenSolution();
solution.putQueen(0);
}
}
八:分支限界
8.1.基本介绍
分支限界法类似于回溯法,也是在问题的解空间上搜索问题解的算法。一般情况下,分支限界法与回溯法的求解目标不同。回溯法的求解目标是找出解空间中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或者极小的解,即在某种意义下的最优解。
分支限界法通常以广度优先搜索或以最小耗费优先的方式搜索问题的解空间树。问题的解空间树是表示问题解空间的一颗有序树,常见的有子集树和排列树。在搜索问题的解空间树时,分支限界法与回溯法的主要区别在于他们对当前扩展节点所采用的扩展方式不同,在分支限界法中,每一个活结点只有一次机会成为扩展节点。活节点一旦成为扩展节点,就一次性产生其所有儿子节点。在这些儿子节点中,导致不可行解或者导致非最优解的儿子节点被舍弃,其余儿子节点被加入活节点表中。此后,从活节点表中取下一节点成为当前扩展节点,并且重复上述节点的扩展过程。这个过程一直持续到找到所需的解或者活节点表为空时为止。
8.2 分支限界法与回溯法的区别
- 回溯法
1)(求解目标)回溯法的求解目标是找出解空间中满足约束条件的一个解或所有解。
2)(搜索方式深度优先)回溯法会搜索整个解空间,当不满条件时,丢弃,继续搜索下一个儿子结点,如果所有儿子结点都不满足,向上回溯到它的父节点。
- 分支限界法
1)(求解目标)分支限界法的目标一般是在满足约束条件的解中找出在某种意义下的最优解,也有找出满足约束条件的一个解。
2)(搜索方式)分支限界法以广度优先或以最小损耗优先的方式搜索解空间。
- 常见的两种分支界限法
a.队列式(FIFO)分支界限法(广度优先):按照队列先进先出原则选取下一个结点为扩展结点
b.优先队列式分支限界法(最小损耗优先):按照优先队列规定的优先级选取优先级最高的结点成为当前扩展结
8.3 分支限界--单源最短路径问题
8.3.1 单源最短路径问题介绍
问题描述:给定带权重的有向图G=(V, E),图中的每一条边都具有非负的长度,求从源顶点s到目标顶点t的最短路径问题。
8.3.2 单源最短路径问题思路
(1) 把源顶点s作为根节点开始进行搜索。对源顶点s的所有邻接顶点,都产生一个分支结点,估计从源点s经该邻接顶点到达目标顶点t的距离作为该分支结点的下界。选择下界最小的分支结点,对该分支结点所对应的顶点的所有邻接顶点继续进行上述的搜索.
(2)下界估算方法:(贪心算法思想)
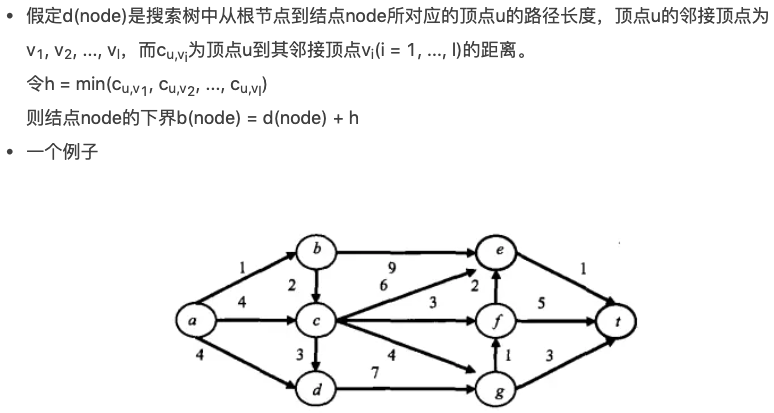
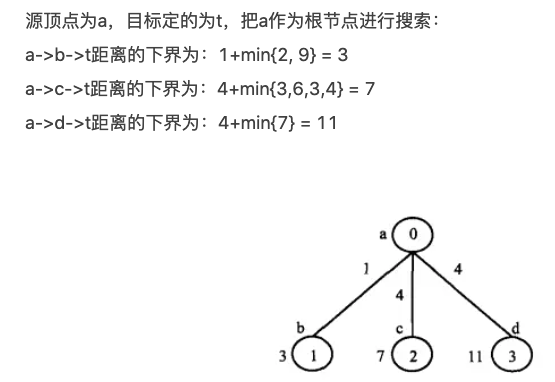
(注意:分支限定算法思想中也隐藏着贪心算法和回溯算法的基本思维)
(3)具体样例说明:
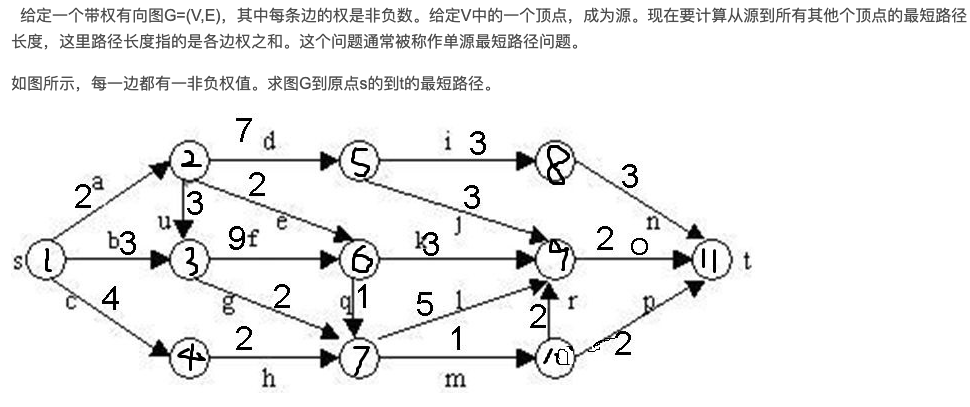
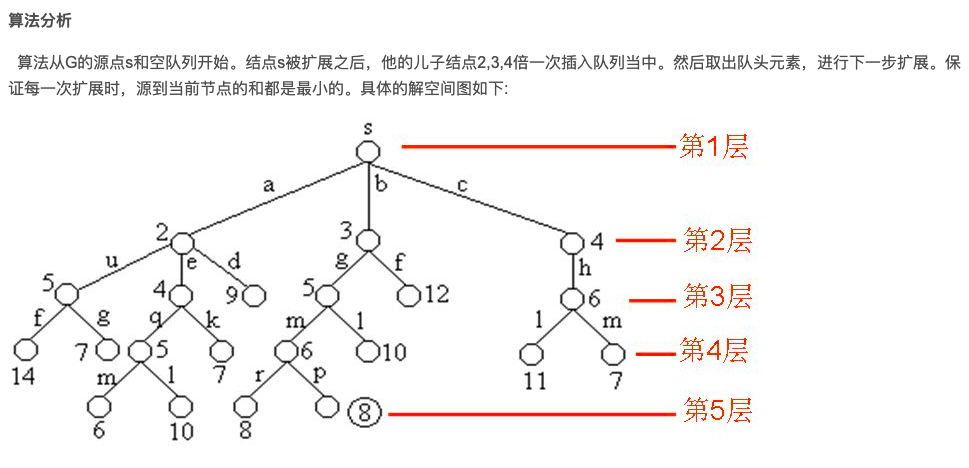

8.3.3 单源最短路径问题代码实现
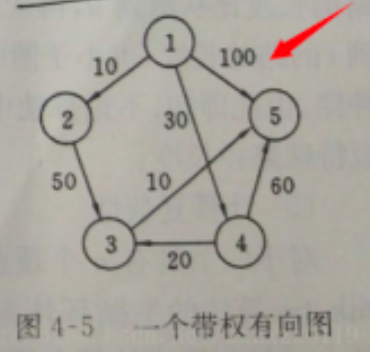
输入:
5
-1 10 -1 30 100
-1 -1 50 -1 -1
-1 -1 -1 -1 10
-1 -1 20 -1 60
-1 -1 -1 -1 -1package temp;
import java.io.BufferedInputStream;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Scanner;
/**
* 分支限界法解决单源最短路径
*/
public class BBShortestPath {
public static void main(String[] args) {
System.out.println("请输入节点个数和节点之间路径长度");
Scanner cin = new Scanner(new BufferedInputStream(System.in));
int n = cin.nextInt();
int[] dist = new int[n+1];
int[] pre = new int[n+1];
int[][] map = new int[n+1][n+1];
for(int i= 1;i<=n;i++) {
for(int j =1;j<=n;j++) {
map[i][j] = cin.nextInt();
}
}
BBShortestPath bbp = new BBShortestPath(n,map,dist,pre);
bbp.ShortestPath(1);
for(int i =2;i<=n;i++) {
System.out.println("源点到" + i + "节点的最短距离是:"+dist[i]);
System.out.println("这个节点的前驱节点是"+ pre[i]);
}
}
private static final int INF = 1000000;
private int n ;
private int[][] map;
private int[] dist,pre; //记录最短距离的数组,以及保存前驱顶点的数组
public BBShortestPath(int n,int[][] map,int[] dist, int[] pre) {
super();
this.n =n;
this.map= map;
this.dist = dist;
this.pre = pre;
}
//最小堆中的元素类 ID表示该活节点所表示的图中的相应的顶点号, length表示源点到改点的距离
private static class MinHeapNode implements Comparable<MinHeapNode>{
private int id;
private int length;
public MinHeapNode(int id, int length) {
super();
this.id = id;
this.length= length;
}
@Override
public int compareTo(MinHeapNode o) { //升序排列
return length > o.length ? 1: (length == o.length ? 0 : -1);
}
}
public void ShortestPath(int s) {
LinkedList<MinHeapNode>heap= new LinkedList<MinHeapNode>();
MinHeapNode now = new MinHeapNode(s, 0);
for(int i=1;i<=n;i++) {dist[i] = INF;}
dist[s] = 0;
while(true) {
for(int j =1; j<= n; j++) {
if(map[now.id][j] !=-1 && now.length+map[now.id][j] <dist[j]) {
dist[j] = now.length+map[now.id][j];
pre[j] = now.id;
MinHeapNode next = new MinHeapNode(j, dist[j]); //加入活节点队列中
heap.add(next);
Collections.sort(heap);
}
}
if(heap.isEmpty())break;
else now = heap.poll();
}
}
}
输出结果

九.参考文献
欧几里德与扩展欧几里德算法
浅议Fibonacci(斐波纳契)数列求解
牛客网-一元多项式求导
递推与递归算法总结
hanoi问题
Java实现hanoi塔
图解快速排序
快速排序
贪心算法
* 十大传统经典算法PDF(https://github.com/zebrama/life-source/tree/master/%E8%B5%84%E6%BA%90/%E5%AD%A6%E4%B9%A0/%E8%AF%BE%E5%A4%96/%E7%BC%96%E7%A8%8B%E8%AF%AD%E8%A8%80)
什么是动态规划
非常好的动态规划总结
最长公共子序列问题
回溯法之八皇后问题
回溯算法
分支限界法详细应用介绍
分支限界法
* 算法设计-Java语言描述
分支限界法总结--例题(01背包,最大团,单源最短路径,装载问题,布线问题)
最后
以上就是忐忑发卡最近收集整理的关于算法设计-最全详细知识总结-递推+递归法+分治法+动态规划+贪心算法+回溯算法+分支法(Java版)传统算法-知识总结-递推+递归+分治+动态规划+贪心算法+回溯算法+分支一:算法基础二.递推三:递归四:分治五:贪心算法六:动态规划七:回溯法八:分支限界九.参考文献的全部内容,更多相关算法设计-最全详细知识总结-递推+递归法+分治法+动态规划+贪心算法+回溯算法+分支法(Java版)传统算法-知识总结-递推+递归+分治+动态规划+贪心算法+回溯算法+分支一:算法基础二内容请搜索靠谱客的其他文章。








发表评论 取消回复