机器学习笔记——决策树

72 阅读 0 评论 48 点赞

我是靠谱客的博主彪壮鞋子，最近开发中收集的这篇文章主要介绍机器学习笔记——决策树，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

昨天是七夕啊，我看了一眼空荡荡的卧室今年还是一个人过七夕，只能

import numpy as npy

????单身的朋友早日脱单，下面正文开始

（本来是昨天发的，结果一个CTRL+Z把文章给我干碎了就只能重写）

什么是决策树(Decision Tree)？

决策树是一种常用的解决分类问题的监督性学习方法，它采用了树形结构就长下面那样

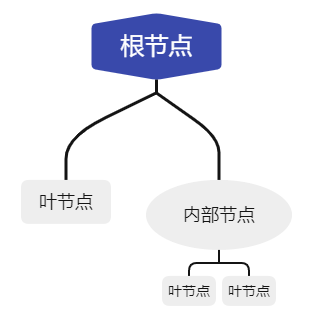
其中根节点是所有样本的全集，只有出边；内部节点是对于某一特征的比较或测试，有一条进边与若干条出边；叶节点代表了决策过后分出的类别，只有一条进边。

当我们预测一个样本的类别时，会从根节点出发，然后通过内部节点对于某一特征的判断去向其子节点，然后重复直到到达叶节点，输出叶节点所表示的类别就是预测值。而在这个过程中我们判断的规则就是通过训练得到的，我们可以将决策树理解为一套if-then-else系统。

举个例子，假设我们得到了一组关于茶的样本，我们要判断它是不是好茶，我们就得从根节点出发

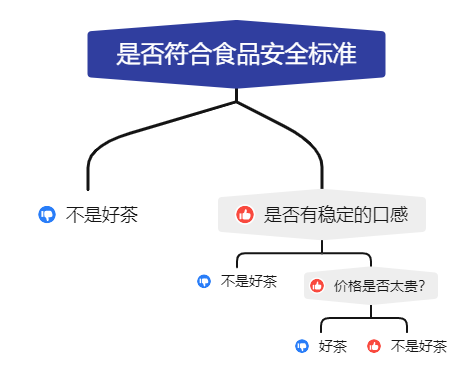这里大拇指朝上表示判断结果为是，大拇指朝下表示判断结果为否。

生成决策树

在我们有了足够数量的样本来训练决策树的时候，我们就会根据这些样本来生成我们的决策树。在这之前我们得先知道一个概念叫做信息熵（entropy）,熵表示的是混乱程度，可以理解为在分类出的子集里面类别的杂乱程度。假设当前样本集合里有n个类别，那其中一个类别i的信息就为而对所有的类别求和并乘上选中那个类别的概率我们就得到了信息熵，所以

计算信息熵的代码如下

了解了信息熵之后我们就得考虑如何生成最佳的决策树，因为对于同样的训练集我们可以生成很多个决策树都适用于这个训练集，而现在我们只去考虑最优的那一棵树，对于其他的我在之后随机森林的文章里会讲到。那么最优的那棵树肯定是在每一个内部节点上都会减少最多的信息熵来让剩下的子集更好分类，也就是会去最大化父节点与其下子节点之间的信息熵的差值，我们会称之为最大化信息增益。而对于离散特征a可能会有M种不同的取值，即a1,a2,a3...am，而如果我们使用特征a对数据集D分类会产生M个分支节点，而Dm就是在数据集D种所有在特征a取值am的样本合集，也就是第M个分支，计算信息增益的公式为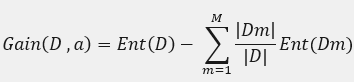

所以生成决策树时我们就会从根节点开始，算出以所有还未使用过的特征分类得到的最大的信息增益，然后基于这个特征建立子节点，然后再在之后的子节点重复这一过程直到信息增益很小或所有特征用完为止。

决策树算法

决策树生成算法有ID3,C4.5,CART等，上面提到的方法是ID3也就是最早提出的决策树算法。

C4.5: 这个算法可以说是ID3的加强升级版，通过对于ID3算法的学习我们会发现可能会出现过拟合（Overfit）的问题，也就是分类分的太细，这样虽然能在训练集中保持很高的正确率但是对于外来数据正确率就会骤降。举个不是很恰当的例子，一家服装店按照三个不同身高的但都比较瘦人制作了三种大小的衣服，之后又来了三个人，有一个身材健硕的顾客来试穿了属于他身高的那一种尺寸的衣服之后会觉得很勒。也就是这三个尺寸是为最开始量尺寸的三个人量身定做的，对于之后来的顾客都穿不了。所以为了避免分类太细这一点C4.5使用了信息增益率来替换信息增益，这样一来在细小的分支信息增益率会很小，在其他地方都与ID3相同。

CART：cart是一种二叉分类树，即一个父节点下只有两个子节点。而生成决策树的基准从信息熵替换成了基尼系数（GINI）。基尼系数公式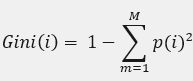p(i)就是样本是第i类的概率，当生成CART树的时候会对于特征a的每个取值分别判断，比如 if a == a1 之后会建立两个子节点分别代表是或否直到剩余样本或基尼系数过小。而生成的规则也是找到基尼系数最小的特征a和其对应的特征值作为最优切分。