信息熵（熵）

参考链接1
参考链接2
熵常用来作为一个集合的信息的量化指标。进一步可以作为一个系统的量化指标或者参数选择的依据。
熵越大代表集合信息的不确定程度越大。（不确定程度与随机变量的概率分布有关，概率分布越均匀，不确定程度越大）

公式

X表示随机变量，H表示熵，p(x)表示事件x发生的概率。

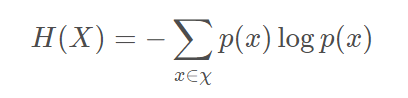
且，0log(0)=0。
当log函数以2为底时，熵的单位是比特（bit）
当数据集中只含有一类数据时，数据的纯度最高，则熵最小，E=0

为何要使用上述公式计算熵呢？因为熵需要满足以下条件：

• 单调性，发生概率越高的事件，其携带的信息量越低；
• 非负性，信息熵可以看作为一种广度量，非负性是一种合理的必然；
• 累加性，即多随机事件同时发生存在的总不确定性的量度是可以表示为各事件不确定性的量度的和，这也是广度量的一种体现。

符合上述三个条件的函数只有如上的形式。

回过头来再看信息熵的公式，其中对概率取负对数表示了一种可能事件发生时候携带出的信息量。把各种可能表示出的信息量乘以其发生的概率之后求和，就表示了整个系统所有信息量的一种期望值。从这个角度来说信息熵还可以作为一个系统复杂程度的度量，如果系统越复杂，出现不同情况的种类越多，那么他的信息熵是比较大的。如果一个系统越简单，出现情况种类很少（极端情况为 1 种情况，那么对应概率为 1，那么对应的信息熵为 0），此时的信息熵较小。

信息增益

两个概率分布的熵的差称为信息增益。
计算公式：原始熵-划分后的数据集子集的熵

• 1）一般而言，信息增益越大，则意味着用属性a来进行划分所获得的"纯度提升"越大，因此，我们可用信息增益来进行决策树的划分属性选择。
• 2）著名的ID3 决策树学习算就是以信息增益为准则来选择划分属性。

决策树

参考资料-写的真挺好的
决策树： 就是通过构建树来进行数据的分类，中间节点表示特征，边表示特征的取值。构建的过程，利用训练集的数据，理想情况每个叶子节点上的的数据都只存在一个类别。因此在使用决策树对输入的测试数据进行分类时，只需要根据每个特征的取值沿着决策树从上而下的走，直到走到叶子结点，当前叶子节点的类别就是该测试数据的预测类别。

决策树的构建(ID3算法)

构建过程采用递归的过程：

1. 找到信息增益最大的特征，该特征作为当前节点
2. 根据该特征对数据集进行划分，构造边。如果划分后的数据集中只有一个类别，则为叶子结点；如果存在多个类别则为中间节点，继续跳到步骤1找新的特征。

递归的结束条件（构建到了叶子结点）：

• 划分后的数据集中只有一个类别
• 已经对所有的特征进行了划分，那么将当前数据集中的出现次数最多的类比作为该叶子节点的类别。

利用决策树进行分类

在进行分类时，

• 需要：已经构建好的决策树、构造决策树的特征标签向量
• 过程：比较测试数据与决策树上的特征对应的数值，递归的执行该过程直到走到叶子结点，则该叶子节点的类别即为测试数据的类别。

决策树的存储

本文后续代码对于构建的决策树使用字典类型存储树的信息
并且使用了python中pickle模块对决策树（字典）数据进行序列化存储到磁盘上。

总结

• 优点：计算复杂度不高，输出结果易于理解
• 缺点：可能出现过度匹配的问题（剪枝处理）
• 适用数据类型：数值型和标称型

过度匹配问题

实就是构造好的决策树太过复杂，叶子结点太多，将这种问题称为过度匹配。
解决方法：剪枝：如果叶子结点存在的信息比较少，可以将该叶子结点删掉，将它并入其他节点。

ID3算法

ID3算法其实无法处理数值型数据，在下面的代码中也只是使用了标称型数据，对于数值型数据可以通过划分区间的方法进行处理。（如参考链接所述）

利用ID3算法构建决策树代码

from math import log


def calcShannonEnt(dataSet):
    '''
    计算给定数据集的熵
    :param dataSet:
    :return:
    '''
    # 1、根据频率计算概率：先计算数据集中每个类别出现的次数，存在字典中
    num = len(dataSet)
    dataDict = {}
    for data in dataSet:
        label = data[-1]
        if label not in dataDict.keys():
            dataDict[label] = 0
        dataDict[label] += 1
    # 2、根据上面计算的频率，计算熵
    shannonEnt = 0.0
    for key in dataDict.keys():
        p = dataDict[key] / float(num)
        shannonEnt += p * log(p, 2)
    return -shannonEnt


def createDataSet():
    dataSet = [[1, 1, 'yes'],
               [1, 1, 'yes'],
               [1, 0, 'no'],
               [0, 1, 'no'],
               [0, 1, 'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels


def splitDataSet(dataSet, axis, value):
    '''
    根据axis=value划分数据集，将axis=value的数据划分出来返回。
    :param dataSet:
    :param axis:
    :param value:
    :return:
    '''
    retDataSet = []
    for data in dataSet:
        if data[axis] == value:
            reducedata = data[:axis]
            reducedata.extend(data[axis + 1:])
            retDataSet.append(reducedata)
    return retDataSet


def chooseBestFeatureTopSplit(dataSet):
    '''
    选择最好的数据集划分方法，
    先使用每个特征和特征取值进行划分，然后计算每个划分的熵
    :param dataSet:
    :return:
    '''
    numfeature = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestFeature = -1
    bestInfoGain = 0.0
    for i in range(numfeature):
        # 1、要获取每个特征的取值
        featureList = [line[i] for line in dataSet]
        featureList = list(set(featureList))
        # 2、对每个特征的每个取值进行划分数据集然后分别计算熵，然后保留与原始熵差最大的，--特征以及其取值进行返回
        for feaValue in featureList:
            # 划分数据集
            dataSetSplit = splitDataSet(dataSet, i, feaValue)
            # 计算新的熵
            entropy = calcShannonEnt(dataSetSplit)
            if bestInfoGain < (baseEntropy - entropy):
                bestInfoGain = baseEntropy - entropy
                bestFeature = i
        return bestFeature


def maxClassNum(classList):
    '''
    计算当前划分后的数据集的类别标签中各个类别的数目，返回最大类别数目的
    :param classList:
    :return: 类别数最多的类别的数目
    '''
    classDict = {}
    for i in classList:
        if i not in classDict.keys():
            classDict[i] = 0
        classDict[i] += 1
    sortedclassDict = sorted(classDict.items(), lambda x: x[1], reverse=True)
    return sortedclassDict[0][0]


def createTree(dataSet, labels):
    '''
    构建决策树,递归函数
    :param dataSet:
    :param labels: 数据集中所有特征的标签
    :return:
    '''
    # 1、首先判断递归是否结束
    classList = [temp[-1] for temp in dataSet]
    # 递归结束条件1：划分后的数据集的所有类别都一致
    if classList.count(classList[0]) == len(classList): return classList[0]
    # 递归结束条件2：所有的特征都用完了，这时虽然没有划分结束，但是也只能返回数目组多的类别作为此时的叶子结点
    if len(dataSet[0]) == 1: return maxClassNum(classList)

    # 2、递归没有结束就继续划分
    # 找到最优划分的特征
    bestFeature = chooseBestFeatureTopSplit(dataSet)
    bestFeatureLabel = labels[bestFeature]
    # 根据最优划分特征将数据集进行划分
    tree = {bestFeatureLabel: {}}
    del (labels[bestFeature])
    feaValue = list(set([line[bestFeature] for line in dataSet]))
    for fea in feaValue:
        subLabel = labels[:]
        tree[bestFeatureLabel][fea] = createTree(splitDataSet(dataSet, bestFeature, fea), subLabel)
    return tree


def classfity(traintree, labelList, testVec):
    '''
    使用在训练集上构造的决策树对测试数据进行分类，思想就是根据测试数据的特征取值沿着决策树向下走，直到走到叶子结点
    :param traintree:
    :param labelList:
    :param testVec:
    :return:
    '''
    firstnode = list(traintree.keys())[0]
    print(labelList)
    labelindex = labelList.index(firstnode)
    sideDict = traintree[firstnode].keys()
    for side in sideDict:
        if testVec[labelindex] == side:
            if type(traintree[firstnode][side]).__name__ == 'dict':
                classResult = classfity(traintree[firstnode][side], labelList, testVec)
            else:
                classResult = traintree[firstnode][side]
    return classResult


def storeTree(tree,filename):
    # 将生成的决策树进行序列化，存储到文件中
    import pickle
    fw = open(filename, 'wb')
    pickle.dump(tree, fw)
    return fw.close()


def readTree(filename):
    # 将磁盘上存储的决策树进行反序列化
    import pickle
    fr = open(filename, 'rb')
    pickle.load(fr)


# 按间距中的绿色按钮以运行脚本。
if __name__ == '__main__':
    dataSet, labels = createDataSet()
    print(dataSet)
    print(labels)
    shannonEnt = calcShannonEnt(dataSet)
    print("数据集的熵为", shannonEnt)

    # 测试划分数据集的函数
    # splitdata = splitDataSet(dataSet, 1, 1)
    # print(dataSet)
    # print(splitdata)

    # 测试chooseBestFeatureTopSplit方法
    # bestFeature = chooseBestFeatureTopSplit(dataSet)
    # print('最好的数据集划分特征：', bestFeature)
    # # 计算划分之后的熵
    # dataSetSplit=splitDataSet(dataSet,bestFeature,0)
    # entroySplit=calcShannonEnt(dataSetSplit)
    # print("划分之后的熵为：",entroySplit)

    tree = createTree(dataSet, labels)
    print(tree)
    # 测试分类函数
    dataSet, labels = createDataSet()
    classres = classfity(tree, labels, [0, 0])
    print(classres)

    # 将决策树进行序列化
    filename='./decisionTree.txt'
    # storeTree(tree,filename)

    # 将磁盘中存储的决策树进行反序列化，
    tree_read=readTree(filename)
    classres = classfity(tree, labels, [0, 0])
    print(classres)

最后

以上就是正直蜜粉为你收集整理的机器学习2——决策树信息熵（熵）决策树的全部内容，希望文章能够帮你解决机器学习2——决策树信息熵（熵）决策树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。