决策树介绍:
决策树分类算法是一种基于实例的归纳学习方法,它能从给定的无序的训练样本中,提炼出树型的分类模型。树中的每个非叶子节点记录了使用哪个特征来进行类别的判断,每个叶子节点则代表了最后判断的类别。根节点到每个叶子节点均形成一条分类的路径规则。而对新的样本进行测试时,只需要从根节点开始,在每个分支节点进行测试,沿着相应的分支递归地进入子树再测试,一直到达叶子节点,该叶子节点所代表的类别即是当前测试样本的预测类别。
一般的,一棵决策树包含一个根结点、若千个内部结点和若千个叶结点;叶结点对应于决策结果,其他每个结点则对应于-一个属性测试;每个结点包含的样本集合根据属性测试的结果被划分到子结点中;根结点包含样本全集。从根结点到每个叶结点的路径对应了一个判定测试序列。决策树学习的目的是为了产生一棵泛化能力强,即处理未见示例能力强的决策树,其基本流程遵循简单且直观的“分而治之”(divide and-conquer)策略,如图所示:
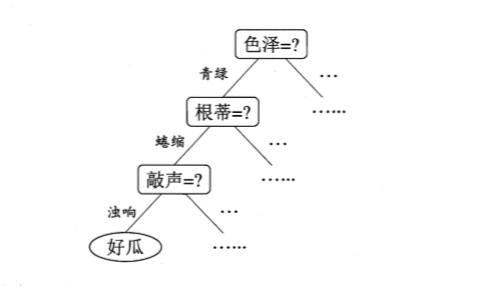
显然,决策树的生成是一个递归过程。在决策树基本算法中,有三种情形会导致递归返回:(1) 当前结点包含的样本全属于同一类别,无需划分; (2)当前属性集为空,或是所有样本在所有属性上取值相同,无法划分;(3)当前结点包含的样本集合为空,不能划分。
在第(2)种情形下,我们把当前结点标记为叶结点,并将其类别设定为该结点所含样本最多的类别;在第(3)种情形下,同样把当前结点标记为叶结点,但将其类别设定为其父结点所含样本最多的类别。注意这两种情形的处理实质不同:情形(2)是在利用当前结点的后验分布,而情形(3)则是把父结点的样本分布作为当前结点的先验分布。
什么是决策树?
让我们从养宠物开始说起
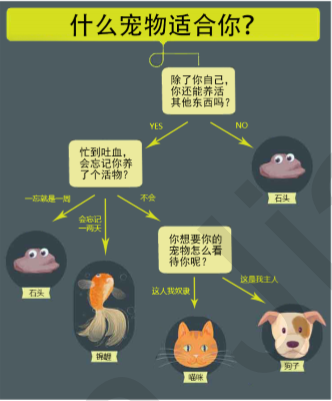
通过上面的例子,我们很容易理解:决策树算法的本质就是树形结构,我们可以通过一些精心设计的问题,就可以对数据进行分类了。在这里,我们需要了解三个概念:
| 节点 | 说明 |
|---|---|
| 根节点 | 没有进边,有出边 |
| 中间节点 | 既有进边也有出边,但进边有且仅有一条, 出边也可以有很多条 |
| 叶节点 | 只有进边,没有出边,进边有且仅有一条。 每个叶节点都是一个类别标签 |
| *父节点和子节点 | 在两个相连的节点中,更靠近根节点的是父节点,另一个则是子节点。两者是相对的。 |
我们可以把决策树看作是一个if-then规则的集合。 将决策树转换成if-then规则的过程是这样的:
由决策树的根节点到叶节点的每一条路径构建一 条规则
路径上中间节点的特征对应着规则的条件,也叶节点的类标签对应着规则的结论。决策树的路径或者其对应的if-then规则集合有一个重要的性质:互斥并且完备。也就是说,每一个实例都被 有且仅有一条路径或者规则所覆盖。这里的覆盖是指实例的特征与路径上的特征一致,或实例满足规则的条件。
决策树的构建准备工作
使用决策树做分类的每一个步骤都很重要,首先我们要收集足够多的数据,如果数据收集不到位,将会导致没有足 够的特征去构建错误率低的决策树。数据特征充足,但是不知道用哪些特征好,也会导致最终无法构建出分类效果 好的决策树。从算法方面来看的话,决策树的构建就是我们的核心内容。决策树如何构建呢?通常,这一过程可以概括为3个步骤:特征选择、决策树的生成和决策树的剪枝。
特征选择:
特征选择就是决定用哪个特征来划分特征空间,其目的在于选取对训练数据具有分类能力的特征。这样可以提高决 策树学习的效率。如果利用一个特征进行分类的结果与随机分类的结果没有很大的差别,则称这个特征是没有分类能力的,经验上扔掉这些特征对决策树学习的精度影响不会很大。
一般而言,随着划分过程不断进行,我们希望决策树的分支节点所包含的样本 尽可能属于同一类别,也就是节点的纯度(purity)越来越高。下面三个图表示的是纯度越来越低的过程,最后一个表示的是纯度最低的状态:
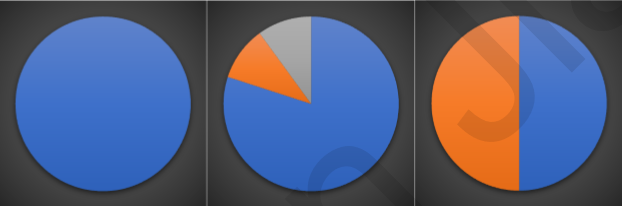
在实际使用中,我们衡量的常常是不纯度。度量不纯度的指标有很多种,比如:熵、增益率、基尼指数。
信息增益:
“信息熵”(information entropy)是度量样本集合纯度最常用的一种指标。假定当前样本集合D中第kt类样本所占的比例为pk (k= 1,2…1.1), 则D的信息熵定义为:
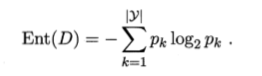
Ent(D)的值越小,则D的纯度越高。
假定离散属性a有V个可能的取值{al,a2…,aV},若使用a来对样本集D进行划分,则会产生V个分支结点,其中第v个分支结点包含了D中所有在属性a上取值为a"的样本,即样本数越多的分支结点的影响越大,于是可计算出用属性a对样本集D进行划分所获得的“信息增益”(information gain):
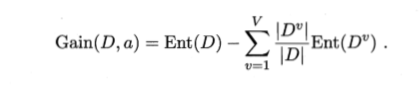
一般而言,信息增益越大,则意味着使用属性a来进行划分所获得的“纯度提升”越大。因此,我们可用信息增益来进行决策树的划分属性选择,即选择属性a*= argmax Gain(D,a)。著名的ID3决策树学习算法就是通过ID3算法实现的
增益率
信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法不直接使用信息增益,而是使用“增益率" (gain ratio)来选择最优划分属性,增益率定义为:
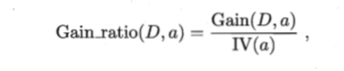
其中
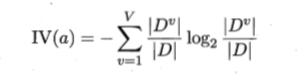
基尼系数
CART决策树使用“基尼指数”(Gini index)来选择划分属性,数据集D的纯度可用基尼值来度量:
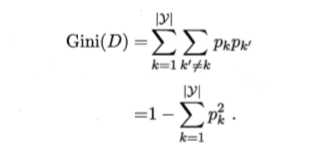
直观来说, Gini(D)反映了从数据集D中随机抽取两个样本,其类别标记直观来说,不一致的概率。因此,Gini(D)越小,则数据集D的纯度越高。属性a的基尼指数定义为:
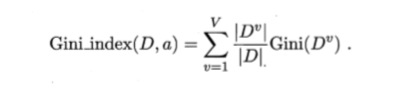
于是,我们在候选属性集合A中,选择那个使得划分后基尼指数最小的属性作为最优划分属性。
代码实现:
#计算香农熵
import numpy as np
def calEnt(dateset):
n=dateset.shape[0];#总行数
iset=dateset.iloc[:,-1].value_counts()#获取种类
p=iset/n;#计算每个种类的概率
ent=(-p*np.log2(p)).sum();#计算熵
return ent;#返回熵的值
#建立数据集(海洋生物为例)
import pandas as pd
def createDateset():
row_date={
'no-surfacing':[1,1,1,0,0],
'flippers':[1,1,0,1,1],
'fish':['yes','yes','no','no','no']
}
dateset=pd.DataFrame(row_date);
return dateset;
#创建一个数据集
dataset=createDateset();
#print('数据集的香农熵为:%s'%(calEnt(dataset)));
#选择最优的列进行切分,返回最佳切分列的索引
def bestSplite(dataset):
baseEnt=calEnt(dataset);#计算信息熵
bestGain=0;#初始化信息增益
asix=-1;#初始化最佳的切分列,标签类
for i in range(dataset.shape[1]-1):#对列进行循环
levels=dataset.iloc[:,i].value_counts().index;#获取当前列的所有值
ents=0;#初始化子节点的信息熵
for j in levels:#对每一列的每一个取值进行循环
childset=dataset[dataset.iloc[:,i]==j]#对每个子节点的dataframe
ent=calEnt(childset);#计算每一个节点的信息熵
ents+=(childset.shape[0]/dataset.shape[0])*ent;#计算当前列的信息熵
# print("信息增益为:%s"%ents)
infoGain=baseEnt-ents;#计算当前列的信息增益
# print("当前的信息增益为:%s"%infoGain)
if infoGain>bestGain:
bestGain=infoGain;
asix=i;
return asix;#返回切分列所在的索引
#按照给定的列切分数据集
#dataset原始的数据集 asix是指定的索引列
#value指定属性值
#测试信息增益
def mysplite(dataset,axis,value):
col=dataset.columns[axis];#获取索引的列的特征名字
redateset=dataset.loc[dataset[col]==value,:].drop(col,axis=1);#将该列去除
return redateset;#返回去除后剩下的列
#构建树
def createTree(dataset):
featlist=list(dataset.columns)#提取出所有的的列
classlist=dataset.iloc[:,-1].value_counts()#获取所有的类标签
#判断是否结束
if classlist[0]==dataset.shape[0] or dataset.shape[1]==1:
#如果所有标签是同一个类的话结束
#如果只剩下最后一列的话结束
return classlist.index[0]#如果是,返回类标签
axis=bestSplite(dataset)#找到当前的最佳标签
bestfeat=featlist[axis]#获取该索引的特征
mytree={bestfeat:{}}#采用字典的形式存储树的信息
del featlist[axis]#删除当前的特征
valuelist=set(dataset.iloc[:,axis])#提取最佳切分列的所有的属性值
for value in valuelist:
#对每一个属性值递归建树
mytree[bestfeat][value]=createTree(mysplite(dataset,axis,value))
return mytree;#返回已经建好的树
#bestSplite(dataset);
mytree=createTree(dataset)
# print(mytree)
#决策树的保存
# np.save('myTree.npy',mytree);
# #将建好的树保存为myTree.npy格式,为了节省时间,建好后的树立马将其保存
# #后续使用直接调用即可
# #打开树,直接调用load()函数即可
# read_mytree=np.load('myTree.npy').item()
# #print(read_mytree)
# #建立分类的函数验证决策树
#iniputtree:已经生成的决策树
#lables:存储选择的最优特征的标签
#testcv:测试数据列表,顺序对应原数据集
def classify(inputTree,lables,testcv):
firstStr=next(iter(inputTree))#获得第一个节点
seconDict=inputTree[firstStr]#获取到下一个字典
feateIndex=lables.index(firstStr)#获取第一个节点所咋IDE索引
for key in seconDict.keys():
if testcv[feateIndex]==key:
if type(seconDict[key])==dict:
classLabel=classify(seconDict[key],lables,testcv);
else:
classLabel=seconDict[key];
return classLabel;
#测试准确率的函数
def acc_classfiy(train,test):
inputTree=createTree(train);#根据训练集生成一个树
lables=list(train.columns)#对数据集的列名称
result=[];#记录结果
for i in range(test.shape[0]):
testvc=test.iloc[i,:-1];
classLable=classify(inputTree,lables,testvc);
result.append(classLable);
test['predict']=result;
acc=(test.iloc[:,-1]==test.iloc[:,-2]).mean();
print(f"模型的准确率为{acc}")
return test;
train=dataset;
test=dataset.iloc[:3,:];
acc_classfiy(train,test);
最后
以上就是壮观黑裤最近收集整理的关于机器学习算法-决策树分类算法的全部内容,更多相关机器学习算法-决策树分类算法内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复