决策树 (Decision Tree)- 机器学习算法

今天来回顾一下一种很古老，又很好理解的机器学习算法--决策树算法，英文名叫Decision Tree。

简介

决策树是一种基本的分类与回归方法，表明它既可以做分类算法，也可以作为回归算法，同时也特别适合集成学习（比如随机森林）。

构建决策树本质上是一个递归的过程。通常是一个递归地选择最有特征，并根据该特征对训练数据进行分割，使得对各个子数据集有一个最好的分类的过程。

在分类问题中，它表示基于特征对实例进行分类的过程，可以认为是if-then规则的集合（可以理解为嵌套的if-then的条件判断过程），也可以认为是定义在特征空间与类空间上的条件概率分布。

决策树工作原理（构造+剪枝）

决策树基本上就是把我们以前的经验总结出来。以下图为例，我们一般会根据条件 "天气"，"温度"， "刮风"，"湿度" 来决定是否去打篮球，结果是："去打篮球"，或 "不去打篮球"。这就是一颗典型的决策树。

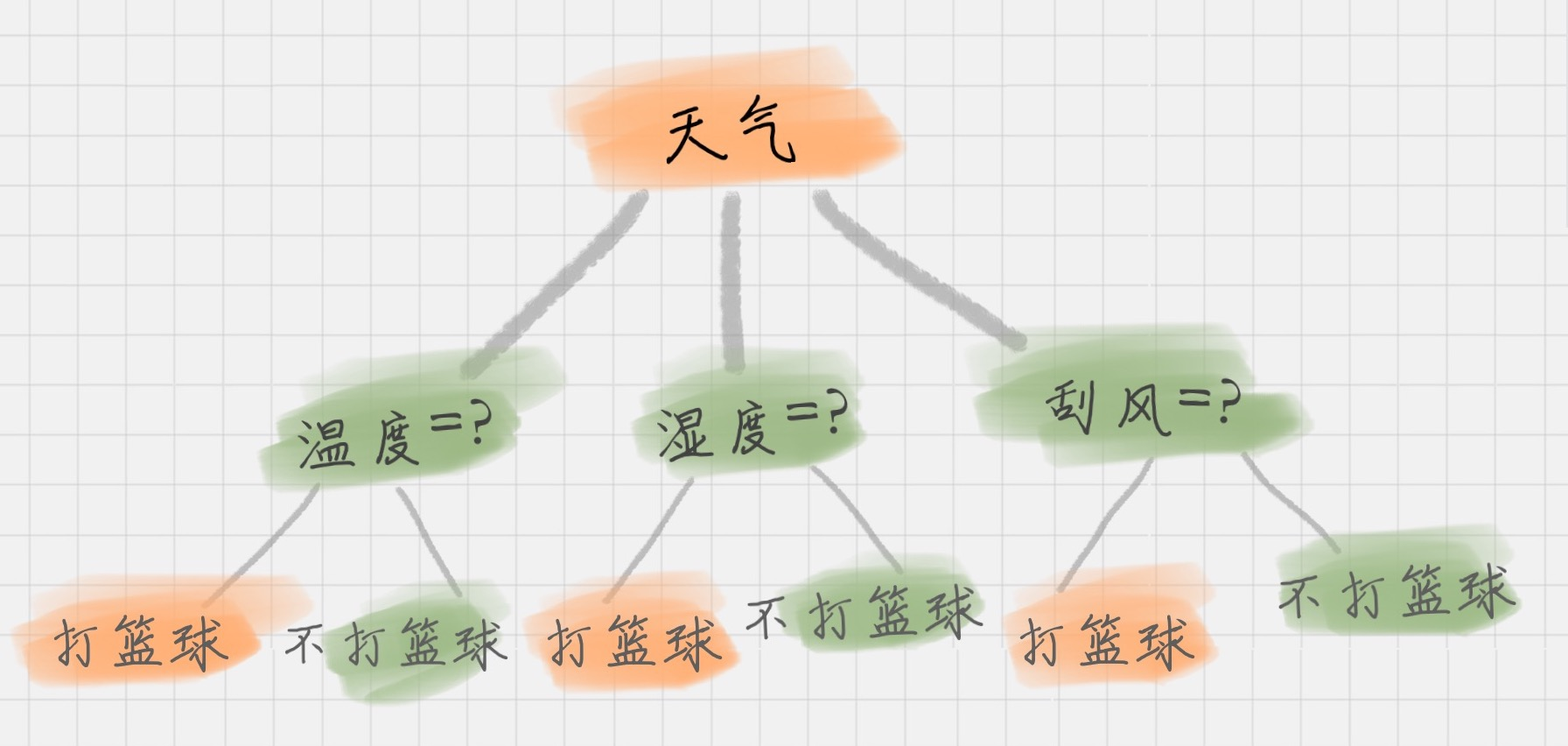
我们在做决策树时，通常包括3个步骤：特征选择，决策树的生成（构造），决策树的修剪（剪枝）

 1.特征选择 

特征选择在于选取对训练数据具有分类能力的特征。

通常特征选择的准则是信息增益（information gain）或信息增益比（information gain rate）。从信息增益的角度来讲，决策树的特征选择实际上是对信息不确定性逐渐下降的过程。

特征选择是决定选用哪个特征来划分特征空间。

2.决策树的生成（构造）

生成决策树的过程就是在不同的节点上选择放置不同特征的过程。构造的过程中，会遇到3种类型的节点

• 根节点：决策树的最顶端。比如，上图中的 "天气" 就处于根节点；
• 内部节点：决策树中间的那些节点。比如，"温度"，"湿度"，"刮风"；
• 叶节点：决策树最底部的节点，也就是决策结果。比如，上图中的 "打篮球" 或 "不打篮球"。

节点之间存在父子关系。比如，根节点会有子节点，子节点会有子子节点，直到叶节点为止。在生成决策树的过程中，需要解决3个问题：选择哪个特征作为根节点，选择哪些特征作为内部节点，什么时候停止并得到目标状态。

3.决策树的修剪（剪枝） 

剪枝，顾名思义就是给决策树 "去掉" 一些判断分支，同时在剩下的树结构下仍然能得到不错的结果。

目的：之所以进行剪枝，是为了防止或减少 "过拟合现象" 的发生，是决策树具有更好的泛化能力。

(需要详细了解 "过拟合现象" 的同学，可以参考下文：https://blog.csdn.net/weixin_42077402/article/details/102619041)

具体作法：去掉过于细分的叶节点，使其回退到父节点，甚至更高的节点，然后将父节点或更高的叶节点改为新的叶节点。

剪枝的两种方法：

• 预剪枝：在决策树构造时就进行剪枝。在决策树构造过程中，对节点进行评估，如果对其划分并不能再验证集中提高准确性，那么该节点就不要继续王下划分。这时就会把当前节点作为叶节点。
• 后剪枝：在生成决策树之后再剪枝。通常会从决策树的叶节点开始，逐层向上对每个节点进行评估。如果剪掉该节点，带来的验证集中准确性差别不大或有明显提升，则可以对它进行剪枝，用叶子节点来代填该节点。

注意：决策树的生成只考虑局部最优，相对地，决策树的剪枝则考虑全局最优。

如何判定决策树的构造有效性

回顾之前是否去打球的例子，决策过程的3个问题中的一个问题是选择哪个属性作为根节点。再回答这个问题之前，让我们想来学习几个概念：纯度，信息熵，条件熵，信息增益（ID3算法），信息增益比（C4.5算法），基尼指数（Cart算法）

>>纯度

数学上，纯度可以用于表示讲目标变量的分歧最小。决策树的构造过程可以理解为寻找纯净划分的过程。

举例说明，假设3个集合：按照纯度的指标来说，集合1（分歧最小）> 集合2> 集合3（分歧最大）。

• 集合1：6次都去打球
• 集合2：4次去打球，2次不去
• 集合3：3次去打球，3次不去

>>信息熵：表示信息的不确定度。

在信息论与概率统计中，随即离散事件出现的概率存在着不确定性。信息熵（Entropy）是表示随机变量不确定性的度量。信息熵越大，随机变量的不确定性就越大，即包含的信息越多。信息熵的计算公式：

     

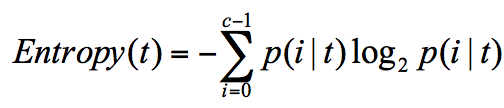
其中，p(i|t) 代表了节点t为分类i的概率。

举例说明，假设有2个集合：

• 集合1：5次打球，1次不打。
• 集合2：3次打球，3次不打。

对于集合1，节点划分为类别"打球"的概率为5/6，划分为类别"不打"的概率为1/6，带入信息熵公式得：

对于集合2，节点划分为类别"打球"的概率为3/6，划分为类别"不打"的概率为3/6，带入信息熵公式得：

可见，信息熵越大，纯度越低。当集合中的所有样本都是均匀混合时，信息熵最大，纯度最低，包含的信息量最大。

>> 条件熵(conditional entropy) H(X|Y)：

定义为特征变量X在给定条件下Y的条件概率分布的信息熵对X的数学期望。

我们在构造决策树时，会基于纯度来构建，经典的 "不纯度" 的判定指标有3种，分别是信息增益（ID3算法），信息增益比（C4.5算法），以及基尼系数（Cart算法）。

>> <ID3算法> 信息增益（Information Gain）

信息增益指的是划分可以带来的纯度的提高，也即信息熵的下降。物理意义表示得知特征X的信息而使得类Y的信息的不确定减少的程度。它的计算公共，表示父节点信息熵减去所有子节点的信息熵:

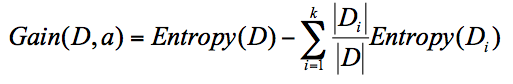
其中，D是父节点，Di是子节点，Gain(D,a)中的a作为D节点的属性选择。

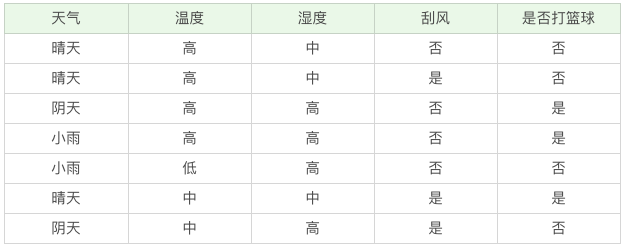
以上表为例说明，假设D天气 = 晴， D1 刮风 = 是，D2 刮风 = 否

D2 刮风 = 否，会有 5 次去打篮球，5 次不打篮球。其中 D1 刮风 = 是，有 2 次打篮球，1 次不打篮球。D2 刮风 = 否，有 3 次打篮球，4 次不打篮球。那么a 代表节点的属性，即天气 = 晴。

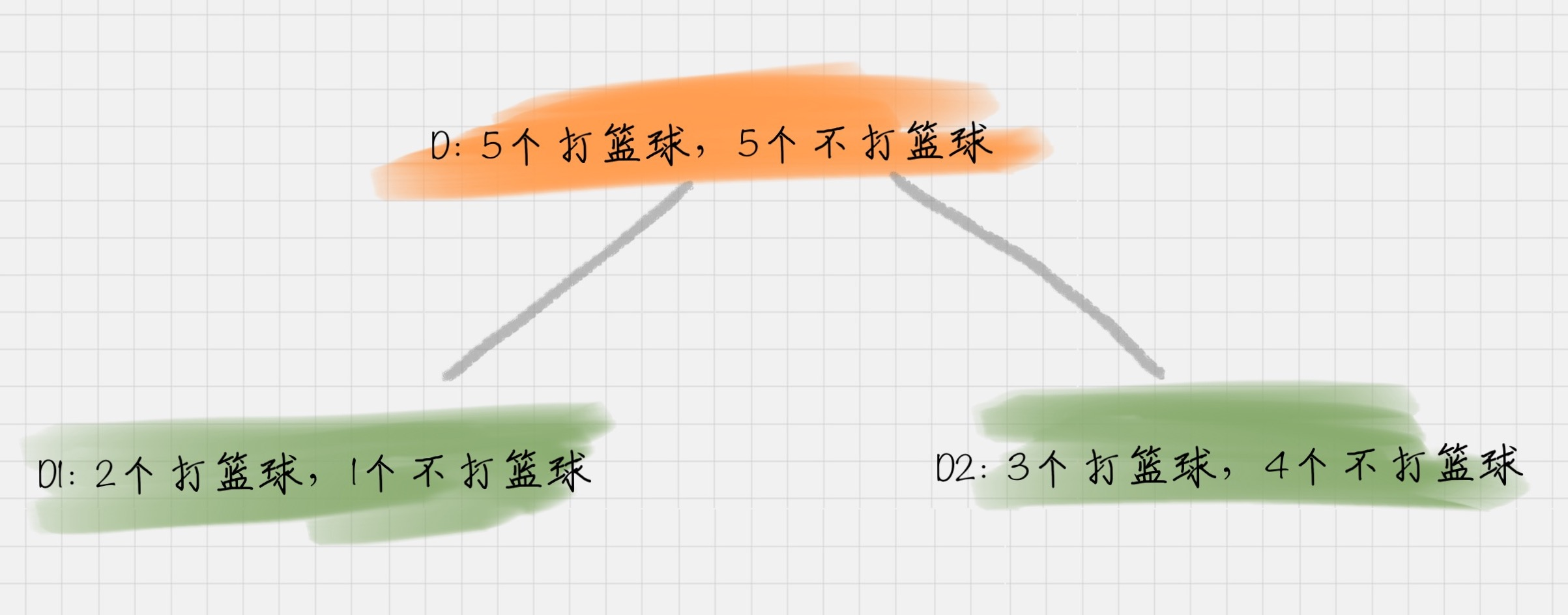
针对图上这个例子，D 作为节点的信息增益为：

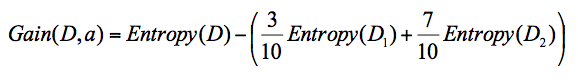
也就是 D 节点的信息熵 -2 个子节点的归一化信息熵。2个子节点归一化信息熵 =3/10 的 D1 信息熵 +7/10 的 D2 信息熵。

我们基于 ID3 的算法规则，完整地计算下我们的训练集，训练集中一共有 7 条数据，3 个打篮球，4 个不打篮球，所以根节点的信息熵是：

如果你将天气作为属性的划分，会有三个叶子节点 D1、D2 和D3，分别对应的是晴天、阴天和小雨。

我们用 + 代表去打篮球，- 代表不去打篮球。

那么第一条记录，晴天不去打篮球，可以记为 1-，于是我们可以用下面的方式来记录 D1，D2，D3：

D1(天气 = 晴天)={1-,2-,6+}

D2(天气 = 阴天)={3+,7-}

D3(天气 = 小雨)={4+,5-}

我们先分别计算三个叶子节点的信息熵：

 

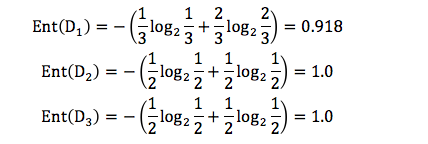
因为 D1 有 3 个记录，D2 有 2 个记录，D3 有2 个记录，所以 D 中的记录一共是 3+2+2=7，即总数为 7。所以 D1 在 D（父节点）中的概率是 3/7，D2在父节点的概率是 2/7，D3 在父节点的概率是 2/7。

那么作为子节点的归一化信息熵 = 3/7*0.918+2/7*1.0+2/7*1.0=0.965。

因为我们用 ID3 中的信息增益来构造决策树，所以要计算每个节点的信息增益。

天气作为属性节点的信息增益为，Gain(D , 天气)=0.985-0.965=0.020。

同理我们可以计算出其他属性作为根节点的信息增益，它们分别为：

Gain(D , 温度)=0.128

Gain(D , 湿度)=0.020

Gain(D , 刮风)=0.020

我们能看出来温度作为属性的信息增益最大。因为 ID3 就是要将信息增益最大的节点作为父节点，这样可以得到纯度高的决策树，所以我们将温度作为根节点。其决策树状图分裂为下图所示：

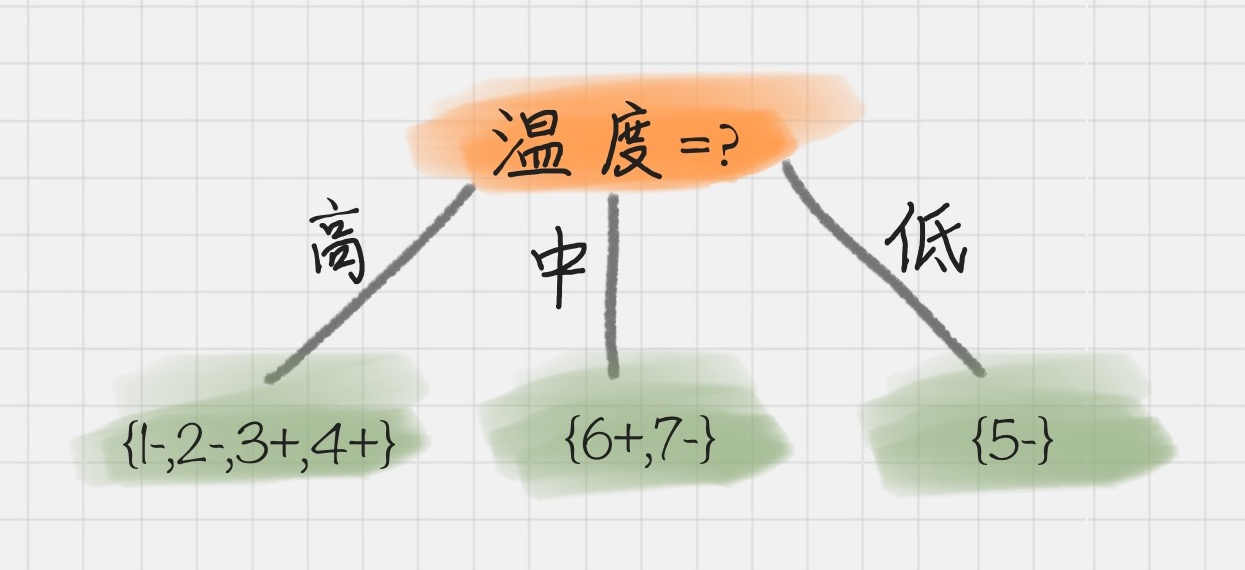
然后我们要将上图中第一个叶节点，也就是 D1={1-,2-,3+,4+}进一步进行分裂，往下划分，计算其不同属性（天气、湿度、刮风）作为节点的信息增益，可以得到：

Gain(D , 天气)=0

Gain(D , 湿度)=0

Gain(D , 刮风)=0.0615

我们能看到刮风为 D1 的节点都可以得到最大的信息增益，这里我们选取刮风作为节点。同理，我们可以按照上面的计算步骤得到完整的决策树，结果如下：

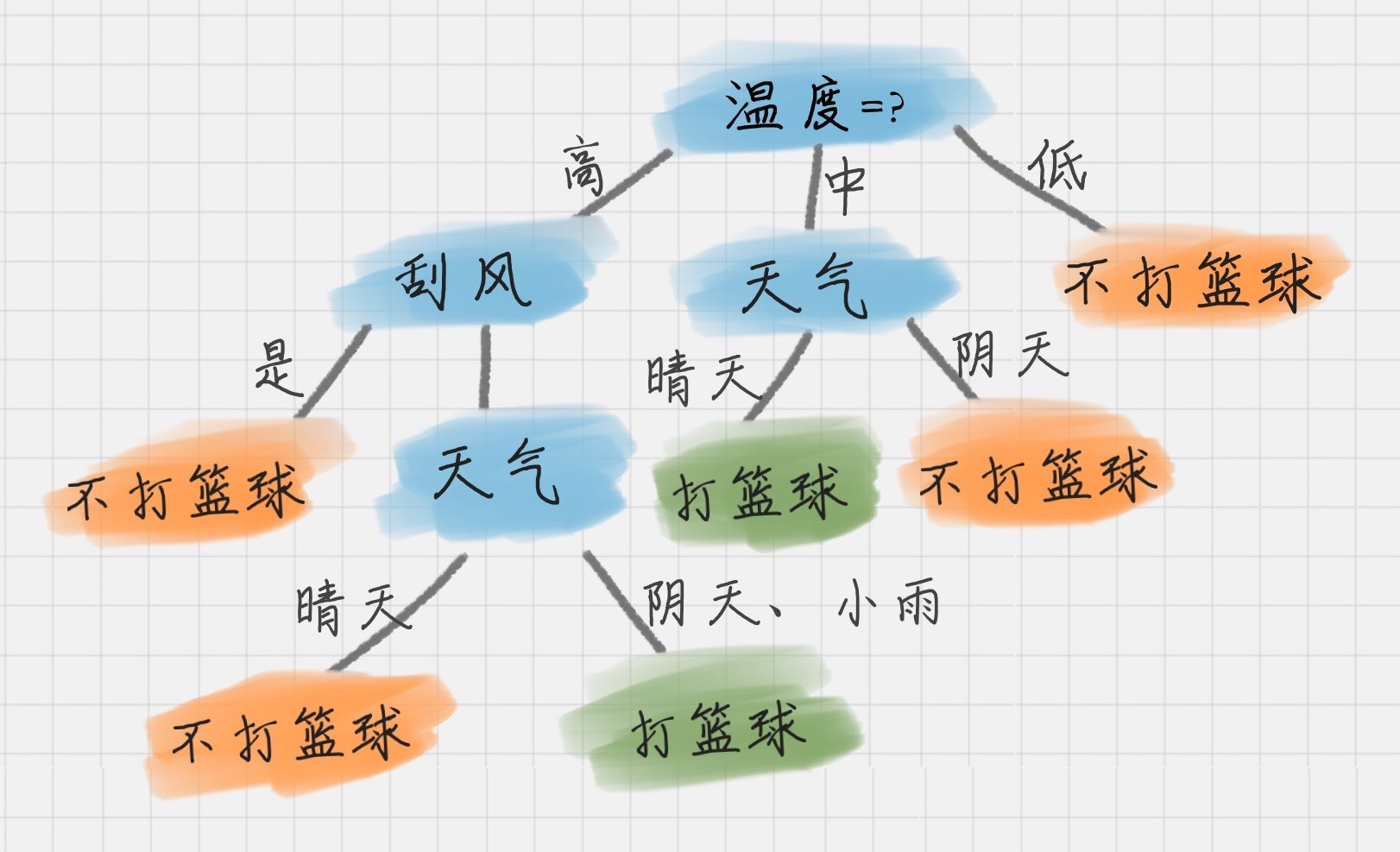
ID3 的算法规则相对简单，可解释性强。同样也存在缺陷，比如我们会发现

•  ID3 算法倾向于选择取值比较多的属性。这样，如果我们把“编号”作为一个属性（一般情况下不会这么做，这里只是举个例子），那么“编号”将会被选为最优属性 。但实际上“编号”是无关属性的，它对“打篮球”的分类并没有太大作用。
• ID3没办法处理连续值，对于连续值的特征无法进行划分；
• ID3无法处理有缺失值的数据；
• ID3无法处理过拟合问题，而决策树很容易出现过拟合；

>>  <C4.5算法> 信息增益比（Information Gain）

1>. 采用信息增益率

因为 ID3 在计算的时候，倾向于选择取值多的属性。为了避免这个问题，C4.5 采用信息增益率的方式来选择属性。信息增益率 = 信息增益 / 属性熵

当属性有很多值的时候，相当于被划分成了许多份，虽然信息增益变大了，但是对于 C4.5 来说，属性熵也会变大，所以整体的信息增益率并不大。

2>. 采用悲观剪枝

ID3 构造决策树的时候，容易产生过拟合的情况。在 C4.5中，会在决策树构造之后采用悲观剪枝（PEP），这样可以提升决策树的泛化能力。

悲观剪枝是后剪枝技术中的一种，通过递归估算每个内部节点的分类错误率，比较剪枝前后这个节点的分类错误率来决定是否对其进行剪枝。这种剪枝方法不再需要一个单独的测试数据集。

3>. 离散化处理连续属性

C4.5 可以处理连续属性的情况，对连续的属性进行离散化的处理。比如打篮球存在的“湿度”属性，不按照“高、中”划分，而是按照湿度值进行计算，那么湿度取什么值都有可能。该怎么选择这个阈值呢，C4.5 选择具有最高信息增益的划分所对应的阈值。

4>. 处理缺失值

针对数据集不完整的情况，C4.5 也可以进行处理。

假如我们得到的是如下的数据，你会发现这个数据中存在两点问题。第一个问题是，数据集中存在数值缺失的情况，如何进行属性选择？第二个问题是，假设已经做了属性划分，但是样本在这个属性上有缺失值，该如何对样本进行划分？

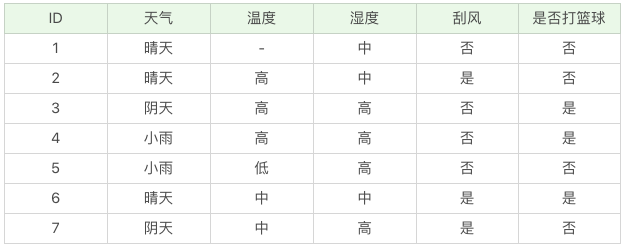
我们不考虑缺失的数值，可以得到温度 D={2-,3+,4+,5-,6+,7-}。温度 = 高：D1={2-,3+,4+}；温度 = 中：D2={6+,7-}；温度 = 低：D3={5-} 。这里 + 号代表打篮球，- 号代表不打篮球。比如ID=2 时，决策是不打篮球，我们可以记录为 2-。

所以三个叶节点的信息熵可以结算为：

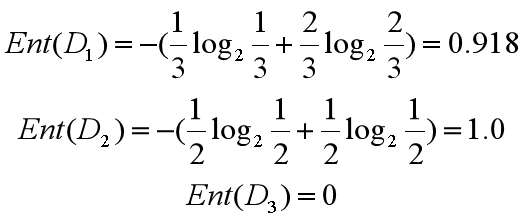
这三个节点的归一化信息熵为 3/6*0.918+2/6*1.0+1/6*0=0.792。

针对将属性选择为温度的信息增益率为：

Gain(D′, 温度)=Ent(D′)-0.792=1.0-0.792=0.208

D′的样本个数为 6，而 D 的样本个数为 7，所以所占权重比例为 6/7，所以 Gain(D′，温度) 所占权重比例为6/7，所以：

Gain(D, 温度)=6/7*0.208=0.178

这样即使在温度属性的数值有缺失的情况下，我们依然可以计算信息增益，并对属性进行选择。

虽然C4.5解决了ID3算法中的几个缺点，但其仍有不足之处：

• C4.5的剪枝不够有效；
• 和ID3一样，C4.5也是生成多叉树，然而计算机中二叉树模型比多叉树效率高很多；
• C4.5只能处理分类问题，不能处理回归为题。

>> <CART算法> 基尼指数

对C4.5进行改进就得到了CART算法，采用二叉树作为树模型的基础结构，通过基尼系数（分类问题）和方差（回归问题）属性来选取最优划分特征。

CART分类树

先引入基尼指数，基尼指数也可以表述数据集D的不确定性，基尼指数越大，样本集合的不确定性就越大，包含的信息量就越大。

       对于给定的样本集，假设有k个类别，第k个类别的概率为Pk，则基尼指数的表达式为：

　　

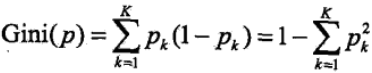
　　对于给定的样本集合D，其基尼指数可以表述为：

　　

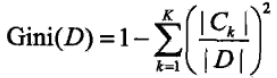
　　在给定特征A的情况下，若集合被特征A的取值给分成D1和D2 ，则在特征A的条件下的基尼指数可以表述为：

　　

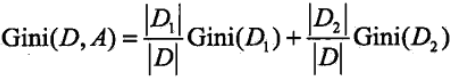
CART回归树

　　CART回归树是CART算法中新引进的用来处理回归问题，其算法流程和CART分类树差不多，但在细节上有写不同，主要是以下两个方面：

　　1）对连续值的处理方式不一样，采用的特征选择属性不一样，在这里采用的是常用的和方差来进行特征选择，其表达式如下：

　　

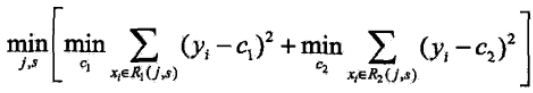
　　对于任意特征A，对应的任意划分点将数据集划分成D1和D2两个部分，寻找到使得D1和D2各自集合的均方误差最小，并且D1和D2的均方误差之和也最小的划分点，该划分点就是该特征最佳的划分点，因此利用和方差选取最优特征时，就是选取使得和方差最小的特征和划分点。

　　2）决策树的预测方式不一样，在分类算法中都是采用叶子结点中数量最多的类别作为输出值，而对于回归问题，一般采用叶子结点中的样本集的均值或者中位数作为输出值，有的还会基于叶子结点中的集合建立线性回归模型来作为输出值。

CART算法虽然进行了大量的改进，但仍然存在一些缺陷：

• 每次用最有特征进行划分，这种贪心算法很容易陷入局部最优。事实上，分类决策不应该由单个特征决定，而是一组特征；
• 样本的敏感性，样本的一点改动足以影响整个数的结构；

决策树的优缺点

决策树的优点：

　　1）决策树简单直观，相比于如神经网络之类的黑盒模型，决策树容易理解，还可以进行可视化；

　　2）基本上不需要做预处理，不需要做归一化，不需要处理缺失值；

　　3）使用决策树进行预测的时间复杂度低，只有O(log2m)，m为样本数；

　　4）即可以处理离散值，也可以处理连续值，无论数对于分类问题还是回归问题；

　　5）可以很容易的处理多分类的问题；

　　6）可以用交叉验证来对决策数进行剪枝，避免过拟合（对于很复杂的决策树，最好配合预剪枝一起处理）；

　　7）对于异常点的容错性好，健壮性高；

决策树的缺点：

　　1）决策树很容易过拟合，很多时候即使进行后剪枝也无法避免过拟合的问题，因此可以通过设置树深或者叶节点中的样本个数来进行预剪枝控制；

　　2）决策树属于样本敏感型，即使样本发生一点点改动，也会导致整个树结构的变化，可以通过集成算法来解决；

　　3）寻找最优决策树是各NP难题，一般是通过启发式方法，这样容易陷入局部最优，可以通过集成算法来解决；　　

　　4）决策树无法表达如异或这类的复杂问题；

小结：

感觉单独用决策树算法的情况不多，决策树大多还是作为集成算法的基学习器来使用的。

 

特别声明：本文中ID3算法，C4.5算法，Cart算法部分引用了 "微笑sun"的博客

参考：

《统计学习方法》 第5章 李航

https://www.cnblogs.com/jiangxinyang/p/9219771.html

https://www.cnblogs.com/pinard/p/6050306.html

https://www.cnblogs.com/molieren/articles/10664954.html

最后

以上就是执着鱼为你收集整理的决策树 (Decision Tree)- 机器学习算法的全部内容，希望文章能够帮你解决决策树 (Decision Tree)- 机器学习算法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。