3.EventMap及其派生类、roots文件

到现在为止，程序acc-tree-stats累积好了构建决策树所需的统计量，程序cluster-phones和compile-questions自动生成好了构建决策树所需的问题集，那么我们就可以开始构建决策树，对三音素GMM的状态进行绑定了。但是在构建决策树之前，我们必须理解清楚决策树构建代码中一个很核心的类：EventMap，只有对EventMap及其派生类理解透彻了，才能深入理解Kaldi决策树构建代码。
　　
　　建议学习Kaldi官方文档《Decision tree internals》、《How decision trees are used in Kaldi》。

EventMap

建议学习Kaldi官方文档《Decision tree internals》的Event maps部分。
　　EventMap是Kaldi决策树状态绑定部分的核心，只有对EventMap理解透彻了，才能看明白构建决策树的代码到底在讲什么。
　　EventType描述三音素和HMM状态信息，其中保存着四对数，其中三对数表示三音素三个位置上的音素分别是什么，剩下的一对数表示HMM状态编号。
　　来看几个int32的别名：　　
　　1. EventKeyType：和EventValueType成对出现；一般表示三音素的位置，当取值为0,1,2时，分别代表三音素从左到右的三个位置；当取值为-1时（一般用常量kPdfClass表示-1），其对应的EventValueType表示的是HMM的第几个状态，也就是HMM state-id。
　　2. EventValueType：和EventKeyType成对出现；当EventKeyType取值为kPdfClass（-1）时，该值表示HMM state-id（一般为0,1,2）；当EventKeyType取0,1,2时，该值表示三音素EventKeyType位置上的音素编号（从1开始对音素进行编号）。
　　3. EventAnswerType：表示发射概率密度函数（p.d.f.）的编号pdf-id；在HMM-GMM模型中，发射概率密度函数就是混合高斯函数；每一个（三音素+HMM state-id）都能确定一个HMM状态，而每个HMM状态都有一个发射p.d.f，所以每个EventType都对应一个pdf-id。状态绑定想做的事就是使多个EventType对应到同一个pdf-id，这样就能减少参数，更好的训练模型。
　　EventType就是四个<EventKeyType, EventValueType>对，其具体的定义是vector<pair<EventKeyType, EventValueType> >。
　　每一个EventType（三音素+HMM state-id）都能确定一个HMM状态，而每个HMM状态都有一个发射p.d.f，我们对模型中所有的p.d.f.进行编号，用不同的pdf-id表示不同的p.d.f，那么从EventType到pdf-id就有一个映射关系，怎么表示这一映射关系？这个时候EventMap就要出场了，EventMap实现了从EventType到pdf-id的映射。
　　具体来讲，EventMap对象的成员方法Map()实现了从EventType到EventAnwserType的映射。
　　举个例子，假设三音素是a/b/c，其音素编号分别为10,11,12，我们想知道该三音素第二个HMM状态的pdf-id是多少（假设答案是1000），下面的代码找出该pdf-id：

EventType e = { {-1, 1}, {0, 10}, {1, 11}, {2, 12} };
EventAnswerType ans;
bool ret = emap.Map(e, &ans); // emap是一个EventMap
// 此时ans为1000

EventMap是保存决策树的一种方法，它是一个多态纯虚类，不能够被实例化。有三个具体的类继承自EventMap，实现了EventMap接口，每种类都有不同的功能，下面我逐一介绍。

ConstantEventMap

ConstantEventMap表示决策树的叶子结点。
　　我们先来思考一下决策树叶子结点的作用和其需要保存什么信息。
　　给定EventType（三音素+HMM state-id，之后都用EventType代表三音素+HMM state-id），我们希望通过决策树得到什么？我们希望通过决策树得到这个EventType对应的p.d.f.的pdf-id。
　　假设我们已经构建好了一个决策树，对某一个EventType，我们从决策树的树根开始问问题，比如左边的音素属于问题集1吗（每个问题集都是一些音素的集合）？右边的音素属于问题集20吗？根据对问题的回答我们就会进入决策树的不同分支，直到到达这个决策树的某一叶子结点，若该叶子结点保存着pdf-id，那么我们就得到了EventType对应的pdf-id。
　　前面我们讲到，可以用EventValueType表示pdf-id，那么叶子结点就只需要保存一个EventValueType类型的变量answer_，用来保存该叶子结点对应的pdf-id即可。

SplitEventMap

SplitEventMap表示决策树的非叶子结点。
　　我们先来思考一下决策树的非叶子结点的作用和其需要保存什么信息。
　　给定一个EventType（三音素+HMM state-id，假设HMM state-id是x），我们开始在中间音素的第x个HMM状态对应的决策树上查找该EventType所属的叶子结点，也就是查找该EventType对应的p.d.f.的pdf-id。对于该EventType，在决策树的每一个非叶子结点，我们都会问一个问题以决定进入该非叶子结点的哪个分支，比如“左边的音素属于问题集1吗？”、“右边的音素属于问题集20吗？”，那么我们该怎么表示“左边”、“右边”呢？根据我们对EventType的理解，可以用EventKeyType类型的变量来表示这个位置信息，我们将其命名为key_——当其取值为0时，我们是对左边的音素问问题；当其取值2时，我们是对右边的音素问问题；因为Kaldi也可以对HMM状态问问题，所以key_可以取kPdfClass(-1)，并且当其取值为kPdfClass时，我们是对HMM状态问问题。
　　在论文中遇见的手工制作的问题类似这样：“左边的音素是鼻音吗？”、“右边的音素是元音吗？”上面我们已经解决了如何描述“左边”、“右边”的问题，另一个问题来了，我们怎么表示“鼻音”、“元音”这些概念呢？其实鼻音就是一些音素的集合，元音也是一些音素的集合。Kaldi中不使用手工制作的问题集，而是使用自动生成的问题集，这些问题集中的每一个问题也都是一些音素的集合。于是我们发现在非叶子结点所问问题的本质其实就是一些音素的集合。这样一来，在每个非叶子结点所问的问题就等价于“第key_个位置的音素属于音素集合1吗？”、“第key_个位置的音素属于音素集合20吗？”类似于EventType那样，我们可以用EventValueType类型的变量表示一个音素，用vector类型的变量表示音素集，我们把这个变量命名为yes_set_。
　　此时，我们在每个非叶子结点所问的问题可以从“左边的音素时鼻音吗？”变成等价的“第key_个位置的音素属于音素集合yes_set_吗？”
　　当第key_个位置的音素属于yes_set_时，我们进入命名为yes_的孩子结点；当第key_个位置的音素不属于yes_set_时，我们进入命名为no_的孩子结点。因为孩子结点可以是叶子结点也可以是非叶子结点，所以用EventMap *来表示指向两个孩子结点的指针。（注意，属于yes_set_和不属于yes_set_两者结合起来等于全部的音素，也就是在每个非叶子结点，无论音素是什么，总能进入某一个分支）
　　综上所述，表示决策树非叶子结点的SplitEventMap所需的数据成员包括：问题所问的位置key_，音素集yes_set_、问题答案属于音素集yes_set_时进入的孩子指针yes_，和问题答案不属于音素集yes_set_时进入的孩子指针no_。
　　实际代码如下所示，注意ConstIntegerSet只是vector的高效表示而已，本质一样。

  EventKeyType key_;
  //  std::vector<EventValueType> yes_set_;
  ConstIntegerSet<EventValueType> yes_set_;  // more efficient Map function.
  EventMap *yes_;
  EventMap *no_;

TableEventMap

一般来说，对每个中间音素的每个状态都要建立一棵决策树进行状态绑定，比如说有63个不同音素，每个音素3个HMM状态，则需要建立63x3=189个决策树。但是Kaldi中想把这189个决策树放进一棵大树里面，这棵大树的189个叶子结点分别是189个决策树的起点；
　　我们随后对这189个叶子结点的每一个进行扩展，每个叶子结点都扩展成一棵决策树，整个完整的大决策树就生成了。当然，这棵大树也用EventMap表示。我个人理解TableEventMap的作用就是更高效的建立扩展之前的这棵大树。当讲到后面的GetStubMap()时应该会体会到这一点。若在每个非叶子结点SplitEventMap上对某个key_问一个问题集yes_set_对大树进行划分，63个点要划分多次才能到达一个叶子结点，可能划分至少5次才能进入一个叶子结点，我们能不能在划分第二次的时候，直接生成多个叶子结点呢？当然可以。注意在SplitEventMap上进行一次划分最多生成两个叶子结点，TableEventMap则可以直接生成多个叶子结点。
　　TableEventMap的数据成员包括进行划分的位置EventKeyType key_，以及指向对其划分后的所有子结点的指针向量std::vector<EventMap*> table_。

Map()

三种EventMap（指ConstantEventMap、SplitEventMap、TableEventMap）具有相同的成员函数接口，但是其具体实现不太一样，具体实现和不同EventMap的功能有关。其中最重要的是搞清楚三种EventMap的Map()方法和Copy()方法做了什么事情。下面我们就逐一讲解。
　　先不看Map()方法的不同实现，我们从统一的接口来看Map()方法完成什么工作。前面讲过，EventMap实现了从EventType到EventValueType到映射，也就是从（三音素+HMM state-id）到pdf-id的映射。Map()的作用是输入EventType，输出pdf-id，其函数声明如下，event是输入的EventType，ans是返回的pdf-id。

bool Map(const EventType &event, EventAnswerType *ans)

在讲解不同的Map()实现之前，我们先讲一下EventMap中用到的静态方法bool Lookup(const EventType &event, EventKeyType key, EventValueType *ans)，输入event和key，输出该event中位置key上保存的内容——若key是kPdfClass(-1)，输出HMM state-id；或key是0,1,2，输出音素编号。
　　决策树是一棵树，树这个数据结构中很重要的思想就是递归。所以关于Map()和Copy()很重要的一点就是递归调用，记住这一点会帮助你进一步理解代码。

• SplitEventMap::Map()。前面讲过，SplitEventMap表示决策树的非叶子结点，在该结点会检查EventType第key_个位置的值（音素编号或HMM state-id）是否属于yes_set_，若属于则进入yes_孩子结点，若不属于则进入no_孩子结点。在SplitEventMap::Map()中，我们首先查找EventType第key_个位置的值value是什么，若该value在yes_set_中，则递归调用yes_孩子的Map()；若该value不在yes_set_中，则递归调用no_孩子的Map()。直到孩子结点是一个叶子结点ConstantEventMap，直接返回保存pdf-id的EventAnswerType answer_。
  举个例子，对于某个中间音素x的决策树，给定中间音素是x的EventType（三音素+HMM state-id）。从该决策树的根结点我们开始进行划分，根结点SplitEventMap保存着自己的key_和yes_set_，我们查看该EventType第key_个位置的值是否在yes_set_中，若在则调用yes_孩子的Map()，若不在则调用no_孩子的Map()；对每个非叶子结点重复这样的划分。假设我们一直进入yes_孩子，则一直递归调用yes_孩子的Map()，直到yes_孩子是一个叶子结点ConstantEventMap，这时就直接把ans置为该叶子结点保存的pdf-id answer_。然后一路返回到树根，这时的ans已经是该EventType对应的pdf-id了，于是我们就根据输入EventType得到了输出EventAnswerType。

  virtual bool Map(const EventType &event, EventAnswerType *ans) const {
    EventValueType value;
    if (Lookup(event, key_, &value)) {
      // if (std::binary_search(yes_set_.begin(), yes_set_.end(), value)) {
      if (yes_set_.count(value)) {
        return yes_->Map(event, ans);
      }
      return no_->Map(event, ans);
    }
    return false;
}

• ConstantEventMap::Map()。前面讲过，ConstantEventMap表示决策树的叶子结点，其保存着该叶子结点所对应的pdf-id。Map()方法的作用就是返回EventType对应的pdf-id，所以当调用ConstantEventMap::Map()时，就直接将ans置为answer_。
  依旧以上面的例子为例，给定EventType，当对决策树的非叶子结点SplitEventMap（后简称SE）一路递归调用Map()到达决策树的叶子结点时，直接返回ConstantEventMap（后简称CE）中保存的answer_即得到了该EventType对应的pdf-id。

  virtual bool Map(const EventType &event, EventAnswerType *ans) const {
    *ans = answer_;
    return true;
     }

• TableEventMap::Map()。在构建扩展之前的决策树时，TableEventMap（后简称TE）也可以作为非叶子结点。在TE结点的Map()方法中，会检查EventType第key_个位置的值tmp是否在table_的范围内，当table_的第tmp个元素存在且不为空时，对TE的第tmp个孩子结点，也就是table_的第tmp个元素递归调用Map()函数，直到到达叶子结点CE，返回该CE的pdf-id answer_。
  TableEventMap的孩子结点数量是固定，为table_.size()，但是这个指针数组不一定都有指向的孩子结点，没有孩子结点的就为null。

  virtual bool Map(const EventType &event, EventAnswerType *ans) const {
    EventValueType tmp;   *ans = -1;  // means no answer
    if (Lookup(event, key_, &tmp) && tmp >= 0
       && tmp < (EventValueType)table_.size() && table_[tmp] != NULL) {
      return table_[tmp]->Map(event, ans);
    }
    return false;
  }

roots文件

在Kaldi中构建决策树时，除了需要累积的统计量和问题集，还需要roots文件。本部分对roots文件进行说明。
　　roots文件指明在决策树的聚类过程中，哪些音素应该共享树根。对放在roots文件同一行的音素共享一个树根，并且roots的每一行需指明下述两件事：

shared or not-shared

“shared”或“not-shared”说的是，对一个音素的不同HMM状态应该建立分开的决策树树根呢，还是让这个音素的不同HMM状态共享一个决策树树根？通过对决策树状态绑定原理的学习，我们知道对一个音素的每个HMM状态都应该建立一个决策树：若一个音素都包含3个HMM状态，则其需要建立三个决策树。若指定”shared”，则Kaldi使三个HMM状态上的决策树共享同一个树根。若指定”not-shared”，则Kaldi为三个HMM状态分别建立决策树树根。(其实差别就在:”not-shared”就是在最初的根节点的位置就对HMM的状态位置提问，然后根据不同的状态划分为三个子树，而”shared”就是在后续的一系列的问题集中，才会出现对HMM的状态位置提问，慢慢的对他们进行划分，可能会出现不止一个关于状态的问题)
　　有人可能会问：如果三个HMM状态共享同一个树根，那么在决策树的每个非叶子结点对左边的音素或右边的音素问问题之后，同一三音素的不同HMM状态不就总是进入同一叶子结点吗？这样一来某一三音素的不同HMM状态对应的pdf-id不就相同了吗？而我们知道某一三音素的不同HMM状态对应的pdf-id一般是不同的。
　　Kaldi采用另外一种机制来解决这个问题：**在每个非叶子结点可以对HMM状态位置问问题！**若某一音素的三个HMM状态共享一个决策树树根，则在该决策树的非叶子结点可以问这种问题：“第kPdfclass(-1)位置的HMM state-id属于{0, 1}吗？”我们知道EventType的第kPdfClass位置保存的值是HMM state-id，当该EventType的HMM state-id是0、1时进入yes_分支；当HMM state-id是2时进入no_分支，这样不同HMM状态就进入不同分支，最后就会进入不同的叶子结点，从而具有不同的pdf-id。

split or not-split

“split”或”not-split”说的是，是否应该对当前的决策树树根进行划分。如果该行指明”split”，则对决策树进行划分；如果该行指明”not-split”，则对该决策树不进行任何划分。
　　下面我们看一个具体的roots文件，上面是roots.txt，下面是对应的roots.int，第一列为行号：

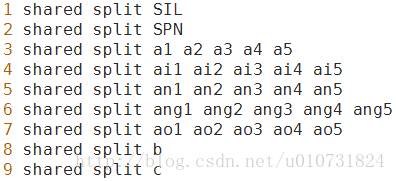
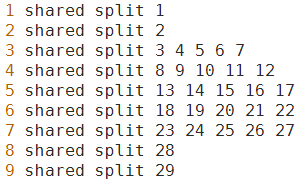
以第三行为例，a1,a2,a3,a4,a5共享一个决策树根，并且该行音素的不同HMM状态也共享(”shared”)一个决策树根。
注意：roots文件中有两种“共享”。一种是roots文件中位于同一行的音素共享同一个决策树；另一种是在每一行前指定”shared”，对不同HMM状态共享同一个决策树。

4.如何构建决策树？

到现在为止，程序acc-tree-stats累积好了构建决策树所需的统计量，程序cluster-phones和compile-questions自动生成好了构建决策树所需的问题集，我们也准备好了roots.int文件，那么我们就可以开始构建决策树，对三音素GMM的状态进行绑定。这次笔记的主要内容是讲解Kaldi如何构建决策树，实现对三音素GMM状态的绑定。
　　在这个笔记中，首先我会介绍构建决策树的主程序build-tree和主函数BuildTree()，然后介绍主函数中用到的核心函数GetStubMap()和SplitDecisionTree()。

建议学习Kaldi官方文档《Decision tree internals》的Classes and functions involved in tree-building部分，官方文档《How decision trees are used in Kaldi》和论文《Tree-Based State Tying For High Accuracy Acoustic Modelling》S.J.Young的第三部分Tree-BasedClustering。

build-tree

• 作用：构建决策树
• 输入：累积的统计量treeacc、问题集questions.qst、roots.int、HMM拓扑topo
• 输出：决策树tree
• 示例：

build-tree $context_opts --verbose=1 --max-leaves=$numleaves 
    --cluster-thresh=$cluster_thresh $dir/treeacc $lang/phones/roots.int 
    $dir/questions.qst $lang/topo $dir/tree

• 过程：

1. 读取roots.int，得到1)vector<vector> phone_sets，其一个元素包含roots.int的一行上的所有音素；2)vector is_shared_root，其一个元素指明该行的音素是否共享三个HMM状态的决策树树根；
   3)vector is_split_root，其一个元素指明是否对该行音素对应的决策树树根进行划分。
2. 读取topo文件，得到保存HMM拓扑结构的对象HmmTopology topo，一般音素的HMM状态为三个，我们实验室只有SIL和SPH的HMM状态为五个。
3. 读取treeacc，得到累积的统计量BuildTreeStatsType stats。
4. 读取questions.qst，得到Questions qo。
5. 调用topo.GetPhoneToNumPdfClasses(&phone2num_pdf_classes)得到vector phone2num_pdf_classes，其元素保存每个音素对应的HMM状态数（前面说了，除了音素SIL和SPH的HMM状态数为5，其他均为3）。
6. 调用BuildTree()，返回保存整个大决策树的EventMap *to_pdf。
7. 用to_pdf初始化对象ContextDependency ctx_dep(N, P, to_pdf)，并将ctx_dep写到文件tree。Kaldi用类ContextDependency对决策树进行封装，其数据成员包含音素宽度N_(=3)、中间音素位置P_(=1)、决策树to_pdf_。

BuildTree()

EventMap *BuildTree(Questions &qopts,
                    const std::vector<std::vector<int32> > &phone_sets,
                    const std::vector<int32> &phone2num_pdf_classes,
                    const std::vector<bool> &share_roots,
                    const std::vector<bool> &do_split,
                    const BuildTreeStatsType &stats,
                    BaseFloat thresh,
                    int32 max_leaves,
                    BaseFloat cluster_thresh,  // typically == thresh.  If negative, use smallest split.
                    int32 P)

建议阅读Kaldi官方文档《Decision tree internals》的 Classes and functions involved in tree-building部分。在build-tree中调用BuildTree()时传递的参数：

    to_pdf = BuildTree(qo,
                       phone_sets,
                       phone2num_pdf_classes,
                       is_shared_root,
                       is_split_root,
                       stats,
                       thresh,
                       max_leaves,
                       cluster_thresh,
                       P);

分块解析： (这是一个总体的流程，建议看一步，然后就往下看一下相应函数的详细解释，一步一步看)

1. 调用GetStubMap()得到初始的决策树EventMap *tree_stub，也就是扩展前的决策树。扩展前的决策树的一个叶子结点对应roots.int中的一行的决策树的树根。后面给出该函数的进一步解释，其中附带GetStubMap()生成的决策树D的图片。建议先跳到后面看懂此函数。
2. 调用FliterStatsByKey()，只把在roots.int中指定为split的音素的统计量留下，把指定为not-split的音素的统计量丢弃。因为我们实验室都是split，所以这一步什么都没做。
3. 调用SplitDecisionTree()，对tree_stub进行扩展，生成整个大的决策树EventMap *tree_split：把tree_stub的每个叶子结点扩展成决策树，对每一个音素生成实际的决策树。后面给出该函数的进一步解释，其中附带相关图片，尽力使该函数的代码变得直观。建议先跳到后面看懂此函数。
4. 调用ClusterEventMapRestrictedByMap()，对tree_split每个音素的决策树上的某些叶子结点进行合并（请参考一开始提到的论文），得到EventMap *tree_clustered。合并前的CE均有不同的answer_，也就是pdf-id不同，合并后某些CE的answer_相同，相同则说明这些叶子结点合并了。这块代码我并没有像之前那样看得很深，只是明白了其作用是什么。有兴趣的读者可以参考我在最后列出的手写笔记草稿的相关部分。
5. 调用RenumberEventMap()对tree_clustered的叶子结点重新编号（从0开始），得到EventMap *tree_renumbered，这就是我们最终得到的完整的决策树。把tree_renumbered返回到主程序build-tree。

GetStubMap()

EventMap *GetStubMap(int32 P,
                     const std::vector<std::vector<int32> > &phone_sets,
                     const std::vector<int32> &phone2num_pdf_classes,
                     const std::vector<bool> &share_roots,
                     int32 *num_leaves_out)

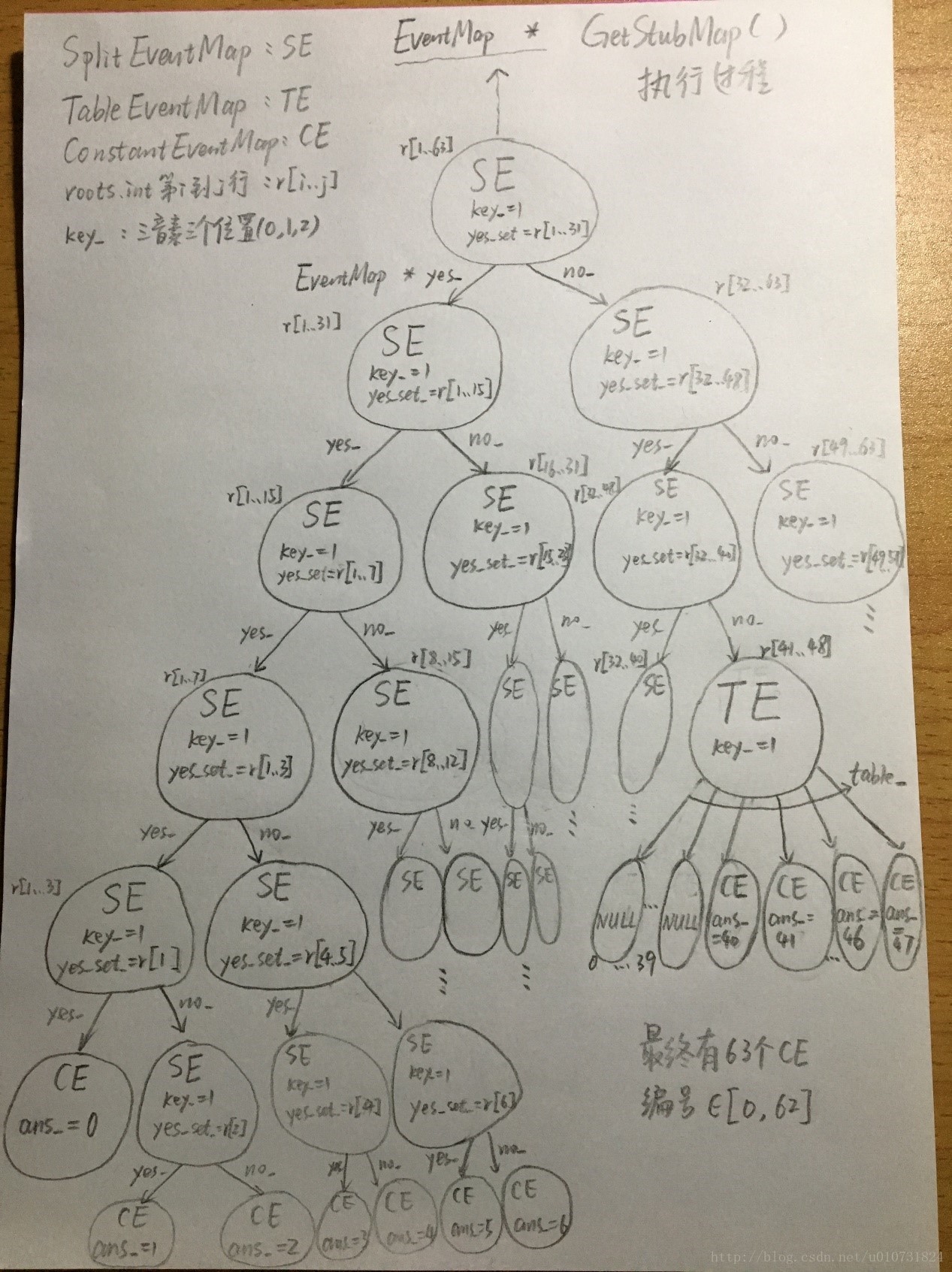
根据从论文中学习到的决策树状态绑定的理论，我们需要对每个音素的每个HMM状态构建一个决策树，假如有63个音素，每个音素有3个HMM状态的话，我们总共应该构建63x3=189个决策树；但是Kaldi中允许不同HMM状态共享同一个决策树根，并且允许在该决策树上的非叶子结点对HMM状态问问题，假如有63个音素，并且每个音素的HMM状态都共享决策树根的话，则我们只需要构建63个决策树。这63个决策树该怎么保存呢？我们可以一个一个写到文件中。但是Kaldi决定把这63个决策树也用一棵决策树D表示——D有63个叶子结点，每个叶子结点都作为63个决策树的树根。
　　GetStubMap()的作用就是构建决策树D，使其每个叶子结点都对应roots.int中的一行的决策树的树根，换句话说，我们本应为roots.int中的一行构建一个决策树d，现在用决策树D的叶子结点保存决策树d的树根。决策树D的作用只是把63个不同的决策树放在一起，随后的代码对决策树D的每个叶子结点进行扩展，在D的叶子结点上构建属于每个音素的实际的决策树。
　　有了上面的理解，按照代码注释里的说法，我们对该函数的作用再重复一遍：GetStubMap()对每一个音素集创建一个初始的叶子结点，一个音素集就是roots.int中的一行中的音素的集合。
　　上面介绍了GetStubMap()的作用，现在对GetStubMap()的代码进行分析，并给出该函数实际得到的决策树的图片，希望对决策树能有一个直观的认识。在阅读该函数的代码时，内心时刻谨记递归调用。
　　以下把ConstantEventMap简称为CE，TableEventMap简称为TE，SplitEventMap简称为SE。
　　该函数的核心代码分块三块，最外层if分支里的代码算一块，最外层else if分支里的代码算一块，最外层else分支里的代码算一块，其作用分别是创建叶子结点CE、创建非叶子结点TE、创建非叶子结点SE。

 if (phone_sets.size() == 1) {  // 创建叶子结点CE 
 
 }else if (max_set_size == 1
             && static_cast<int32>(phone_sets.size()) <= 2*highest_numbered_phone) {
             //创建非叶子结点TE
  } else {//创建非叶子结点SE

  }
  

phone_sets的一个元素是roots.int的一行上的全部音素，以我们实验室为例，roots.int有63行，则递归调用的最外层的GetStubMap()的phone_sets有63个元素。

else {
     // Do a split.  Recurse.
     size_t half_sz = phone_sets.size() / 2;//把phone_sets等分成前后两份
     std::vector<std::vector<int32> >::const_iterator half_phones =
         phone_sets.begin() + half_sz;
     std::vector<bool>::const_iterator half_share =
         share_roots.begin() + half_sz;
     std::vector<std::vector<int32> > phone_sets_1, phone_sets_2;
     std::vector<bool> share_roots_1, share_roots_2;
     phone_sets_1.insert(phone_sets_1.end(), phone_sets.begin(), half_phones);
     phone_sets_2.insert(phone_sets_2.end(), half_phones, phone_sets.end());
     share_roots_1.insert(share_roots_1.end(), share_roots.begin(), half_share);
     share_roots_2.insert(share_roots_2.end(), half_share, share_roots.end());
 //将音素集分为两份，将share_roots分为两份
     EventMap *map1 = GetStubMap(P, phone_sets_1, phone2num_pdf_classes, share_roots_1, num_leaves_out);
     EventMap *map2 = GetStubMap(P, phone_sets_2, phone2num_pdf_classes, share_roots_2, num_leaves_out);
 //对这两部分递归调用GetStubMap()得到两个子树map1和map2；
     std::vector<EventKeyType> all_in_first_set;
     for (size_t i = 0; i < half_sz; i++)
       for (size_t j = 0; j < phone_sets[i].size(); j++)
         all_in_first_set.push_back(phone_sets[i][j]);
     std::sort(all_in_first_set.begin(), all_in_first_set.end());
     KALDI_ASSERT(IsSortedAndUniq(all_in_first_set));
     return new SplitEventMap(P, all_in_first_set, map1, map2);
   }　　

我们先来看最外层的else分支的代码。因为一开始phone_sets.size()不为1而是63，并且max_set_size不为1（因为roots.int中有的行的音素数大于1），所以一开始我们进入的是else分支。一开始在else分支中，我们把phone_sets等分成前后两份，前一半phone_sets_1包含roots.int的前31行，后一半phone_sets_2包含roots.int的后32行；然后对这两部分递归调用GetStubMap()得到两个子树map1和map2；递归调用返回之后，我们创建一个非叶子结点SE，令其key_是1（也就是三音素的中间音素，记得我们要为每一个中间音素构建一棵决策树），其yes_set_是phones_sets的前一半phone_sets_1所包含的全部音素，其yes_孩子结点指向由phone_sets_1生成的子树，其no_孩子结点指向由phone_sets_2生成的子树。我们用SE把phone_sets中的音素分为了两份。
　　扩展上面的过程，我们对phone_sets_1递归调用GetStubMap()会发生什么？我们依旧会进入else分支，对phone_sets_1进行二等分，然后创建一个新的SE，其key_为1，其yes_set_是phone_sets_1的前一半（也就是phone_sets的前1/4），其yes_孩子指向由phone_sets_1的前一半生成的子树，其no_孩子结点指向由phone_sets_1的后一半生成的子树。对phone_sets_2递归调用GetStubMap()，对phone_sets_1的前一半、后一半递归调用GetStubMap()……

if (phone_sets.size() == 1) {  // there is only one set so the recursion finishes.
     if (share_roots[0]) {  // if "shared roots" return a single leaf.
       return new ConstantEventMap( (*num_leaves_out)++ );
     } else {  //因为我们的roots.int中的每一行都指定shared，所以这边先不考虑shared为false的情况
     }
   } 

随着递归调用的深度越深，我们不断生成新的SE对phone_sets进行划分，直到GetStubMap()的参数phone_sets只包含一个元素（也就是只包含roots.int中的一行），这时，我们进入最外层的if分支。（在这里我们假设roots.int中的每一行都指定shared，所以我们只考虑最外层if分支里的if分支，而不考虑最外层if分支里的else分支。）进入最外层的if分支所干的事情就是创建一个叶子结点CE，并设该叶子结点的answer_为num_leaves_out，也就是设该叶子结点的pdf-id为num_leaves_out。假设此时phone_sets只包含的一个元素是roots.int的第一行，我们生成第一个CE，此时num_leaves_out为0，则该CE的answer_为0。

else if (max_set_size == 1
             && static_cast<int32>(phone_sets.size()) <= 2*highest_numbered_phone) {
     // create table map splitting on phone-- more efficient.
     // the part after the && checks that this would not contain a very sparse vector.
     std::map<EventValueType, EventMap*> m;
     for (size_t i = 0; i < phone_sets.size(); i++) {
       std::vector<std::vector<int32> > phone_sets_tmp;
       phone_sets_tmp.push_back(phone_sets[i]);
       std::vector<bool> share_roots_tmp;
       share_roots_tmp.push_back(share_roots[i]);
       EventMap *this_stub = GetStubMap(P, phone_sets_tmp, phone2num_pdf_classes,
                                        share_roots_tmp,
                                        num_leaves_out);
       KALDI_ASSERT(m.count(phone_sets_tmp[0][0]) == 0);
       m[phone_sets_tmp[0][0]] = this_stub;
     }
     return new TableEventMap(P, m);

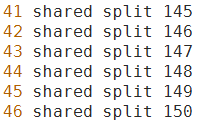
那么TableEventMap有什么作用呢？从上面的过程我们发现，每次划分我们只能创建两个孩子结点，包含63个元素的phone_sets要划分5次才能到达第一个叶子结点，太慢了。我们的目的是创建63个叶子结点，每个叶子结点保存roots.int中的一行，随后对这63个叶子结点进行扩展，构建真正的决策树。那么当某一次递归调用GetStubMap()时我们发现phone_sets的size()不为一但是其每一个元素只包含一个音素，这时我们进入最外层的else if分支，生成一个TE，令其key_为1。假设此时的phone_sets中保存的是roots.int的第41行到第46行，如下图所示，则生成的TE的table_包含150个元素，第0到144个都为NULL，第145到150个都是CE，我们一下子生成了6个叶子结点，比用SE划分快多了。

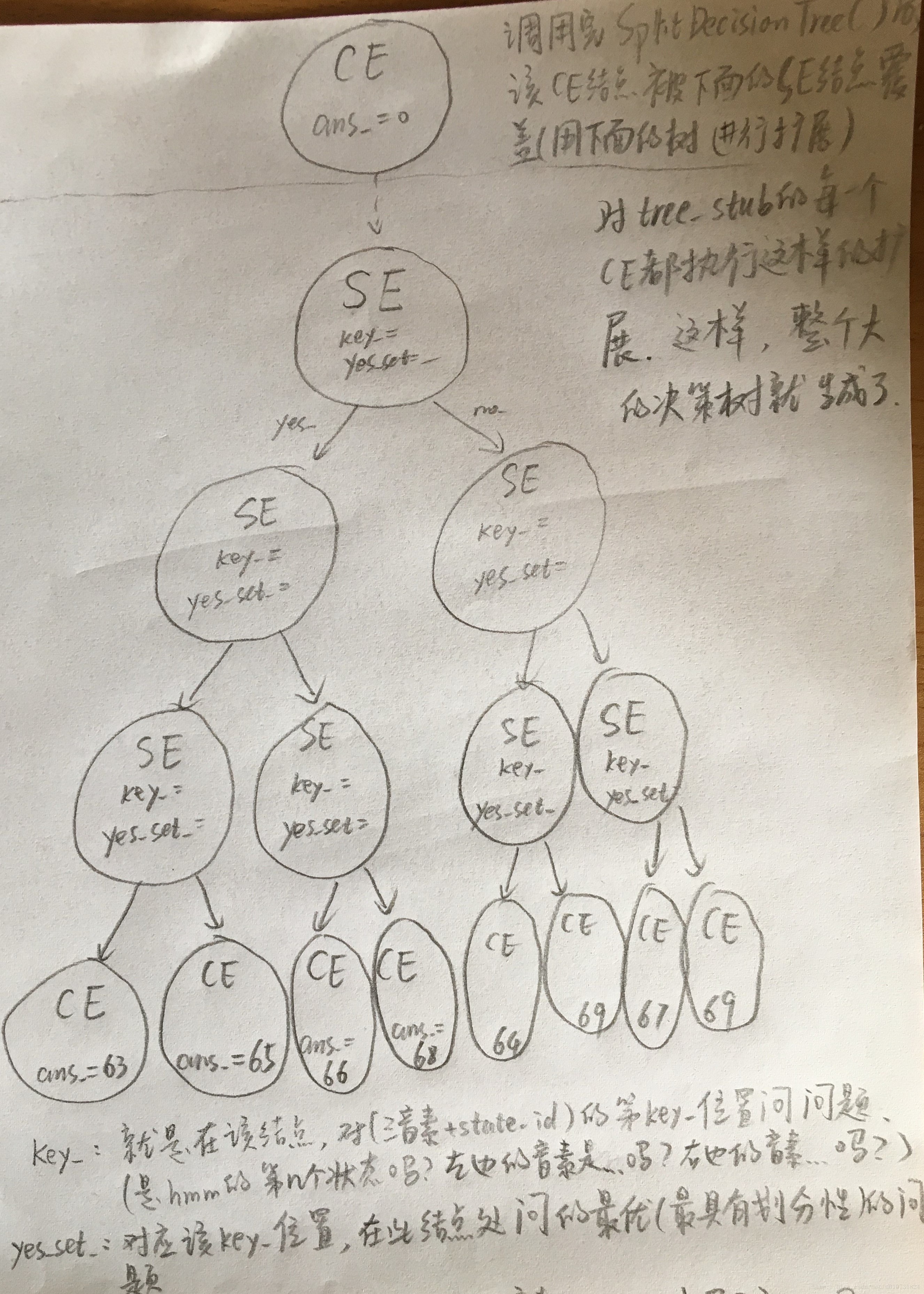
调用GetStubMap()生成的最终的决策树D大概如下图所示，这样我们就为roots.int中的63行的每一行生成了一个叶子结点，随后把这63个叶子结点扩展成各自的决策树，我们就把63个决策树放在一个大的决策树中。

SplitDecisionTree()

EventMap *SplitDecisionTree(const EventMap &input_map,
                            const BuildTreeStatsType &stats,
                            Questions &q_opts,
                            BaseFloat thresh,
                            int32 max_leaves,  // max_leaves<=0 -> no maximum.
                            int32 *num_leaves,
                            BaseFloat *obj_impr_out,
                            BaseFloat *smallest_split_change_out)

参数input_map就是扩展前的决策树tree_stub，其一个叶子结点表示一个音素（确切来说是roots.int中同一行的音素集合，但因为其共享同一个决策树，我们暂且称该音素集为一个音素，便于理解、陈述）。我们现在要对tree_stub的每个叶子结点、也就是每个音素构建一棵决策树，实现状态绑定，减少GMM参数。我们对决策树持续进行划分，直到总的叶子结点数目到达max_leaves，或者所有叶子结点中的最优划分带来的最大似然提升都小于thresh。

• 首先调用SplitStatsByMap()，根据tree_stub对stats进行划分得到split_stats，将对应到同一个叶子结点的统计量放在一起。以我们实验室为例，roots.int包含63行，tree_stub包含63个叶子结点，则对stats划分后，split_stats包含63个元素。对tree_stub的每一个叶子结点、也就是每一个音素初始化一个DecisionTreeSplitter对象，使用这个对象构建对应音素的决策树。我们注意到初始化DecisionTreeSplitter对象时传递的参数包括属于该音素的统计量、问题集。有这两者我们就可以构建起决策树。最终的builders包含63个DecisionTreeSplitter且一直包含63个DecisionTreeSplitter。。
  　　以下将DecisionTreeSplitter简称为DTS。
  　　在初始化每一个DTS时，都会找到这个DTS对应的叶子结点的最优化分（DTS.FindBestSplit()）：首先对于EvenType的每一个key（-1，0，1，2），在该key对应的问题集中（由q_opts给出每个key的问题集）找到一个问题，使得对叶子结点划分后获得的似然提升最大；现在对每个key都找到了一个似然提升，然后比较这几个key的似然提升，找出其中的最大似然提升，将DTS的key_设置为似然提升最大的key，将DTS的yes_set_设置为该key_上取得最大似然提升的问题。也就是说，我们在这个DTS问问题“第key_个位置的音素属于yes_set_吗？”对DTS进行划分。
  　　因为我们要对决策树进行持续划分，所以DTS还保存着指向两个子树的指针DTS *yes_, *no_。当第key_个位置的音素属于yes_set_时进入yes_子树，否则进入no子树。
  　　在本笔记中我就不详细介绍DTS了，其学习思路和笔记（二）中对TreeClusterer的介绍一样：先看该类有哪些数据成员，然后看该类的构造函数都完成什么初始化工作，最后看其主要的成员方法完成什么工作。在下面我会附一张DTS的手写笔记草稿，希望其有一定启发。

  std::vector<DecisionTreeSplitter*> builders;
 {  // set up "builders" [one for each current leaf].  This array is never extended.
   // the structures generated during splitting remain as trees at each array location.
   std::vector<BuildTreeStatsType> split_stats;
   SplitStatsByMap(stats, input_map, &split_stats);
   KALDI_ASSERT(split_stats.size() != 0);
   builders.resize(split_stats.size());  // size == #leaves.
   for (size_t i = 0;i < split_stats.size();i++) {
     EventAnswerType leaf = static_cast<EventAnswerType>(i);
     if (split_stats[i].size() == 0) num_empty_leaves++;
     builders[i] = new DecisionTreeSplitter(leaf, split_stats[i], q_opts);
   }
 }

• 把63个决策树（builders）放在一起比较，每次对似然提升最大的叶子结点（此时结点都是DTS）进行划分（builders[i]->DoSplit()），这种策略通过优先队列实现。划分具体就是指，对处于叶子位置的DTS找到第key_个位置和在该位置所问的问题yes_set_，同时将该DTS上的统计量根据划分结果分配到两个孩子DTS yes_和no_。我们对所有的builders持续进行划分，在tree_stub的每个叶子结点就生成了一棵结点全是DTS的树。

  {  // Do the splitting.
    int32 count = 0;
    std::priority_queue<std::pair<BaseFloat, size_t> > queue;  // use size_t because logically these
    // are just indexes into the array, not leaf-ids (after splitting they are no longer leaf id's).
    // Initialize queue.
    for (size_t i = 0; i < builders.size(); i++)
      queue.push(std::make_pair(builders[i]->BestSplit(), i));
    // Note-- queue's size never changes from now.  All the alternatives leaves to split are
    // inside the "DecisionTreeSplitter*" objects, in a tree structure.
    while (queue.top().first > thresh
          && (max_leaves<=0 || *num_leaves < max_leaves)) {
      smallest_split_change = std::min(smallest_split_change, queue.top().first);
      size_t i = queue.top().second;
      like_impr += queue.top().first;
      builders[i]->DoSplit(num_leaves);
      queue.pop();
      queue.push(std::make_pair(builders[i]->BestSplit(), i));
      count++;
    }
     }

• 对tree_stub的每个叶子结点，我们通过调用builders[i]->GetMap()得到由EventMap表示的属于该音素的决策树。生成好属于每个音素的决策树之后，我们对tree_stub进行扩展，把tree_stub种表示每个音素的叶子结点替换成属于这个音素的决策树EventMap，这就是input_map.Copy(sub_trees)完成的工作。于是，完整的大决策树就生成了。

  EventMap *answer = NULL;
  {  // Create the output EventMap.
    std::vector<EventMap*> sub_trees(builders.size());
    for (size_t i = 0; i < sub_trees.size();i++) sub_trees[i] = builders[i]->GetMap();
    answer = input_map.Copy(sub_trees);
    for (size_t i = 0; i < sub_trees.size();i++) delete sub_trees[i];
}

下面有两幅图片，第一幅表示对tree_stub的第一个叶子结点构建出的由DTS表示的决策树，第二幅表示对DTS表示的决策树的树根(builders[0])调用GetMap()后得到的由EventMap表示的决策树。希望能让大家对每个音素的决策树构建过程有一个直观的认识：

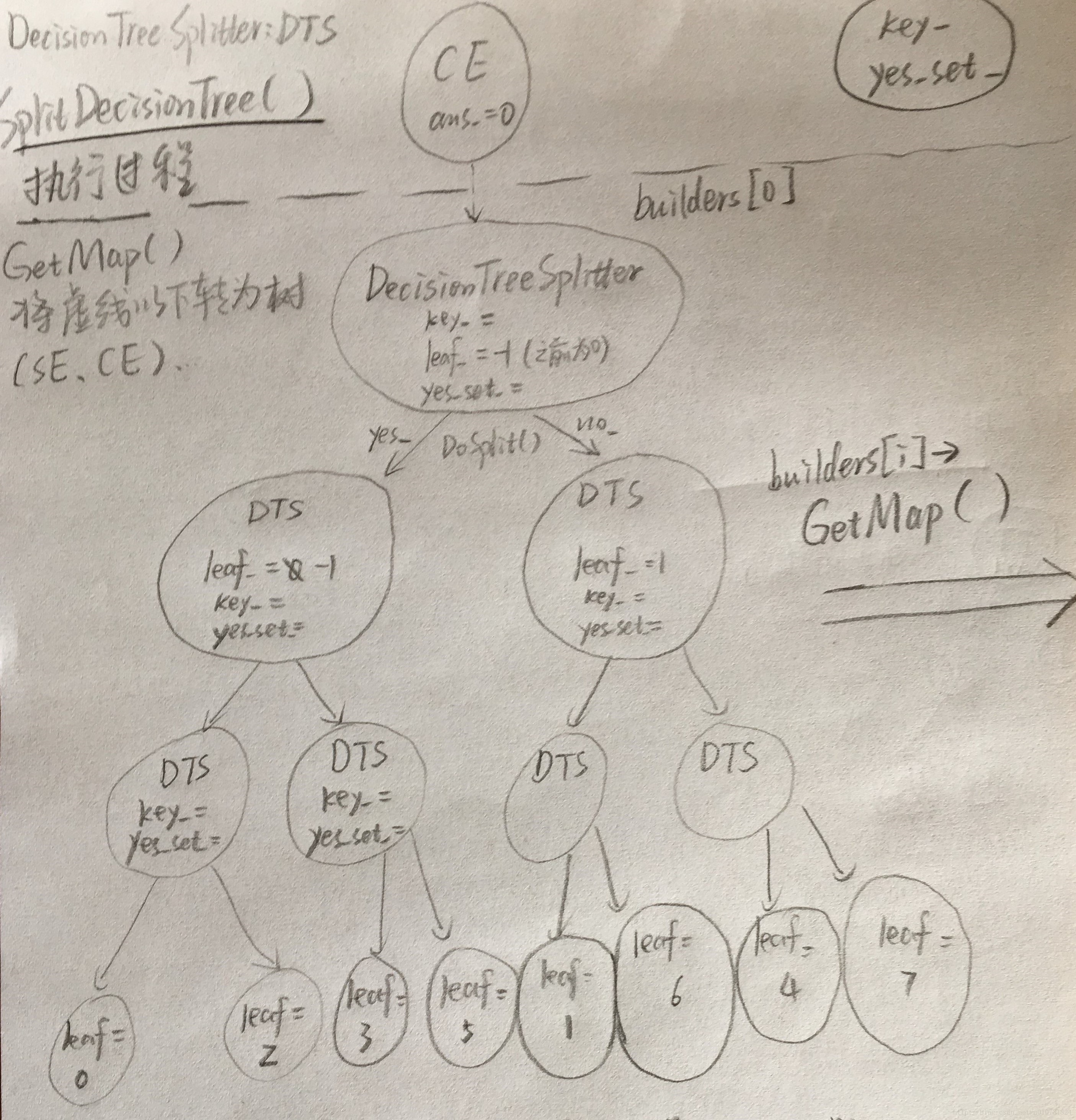
调用完SplitDecisionTree（）后，该CE结点被下面的SE结点覆盖，也就是用下面的树进行扩展。

key的值：就是指对EventType中第几个位置的值进行提问，（-1代表状态，0代表左音素，1代表中间音素，2代表右边的音素）

yes_set：对应该key位置，在此结点处问的最优，也就是最具有划分性的问题。

参考：

开拓师兄的博客。

最后

以上就是美满白羊为你收集整理的Kaldi决策树状态绑定学习笔记（二）3.EventMap及其派生类、roots文件4.如何构建决策树？参考：的全部内容，希望文章能够帮你解决Kaldi决策树状态绑定学习笔记（二）3.EventMap及其派生类、roots文件4.如何构建决策树？参考：所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。