决策树的预剪枝
优秀的决策树:
优秀的决策树不仅对数据具有良好的拟合效果,而且对未知的数据具有良好的泛化能力,优秀的决策树具有以下优点:
- 深度小
- 叶节点少
- 深度小并且叶节点少
拟合分为:过拟合和欠拟合
- 过拟合:训练误差低,测试误差大,即对已知训练数据拟合很好,但是未知数据的预测能力不好,训练出来的模型结构一般较复杂。
- 欠拟合:训练误差高,测试误差低,即对已知的训练数据的拟合误差要大于未知数据的,训练出来的模型过于简单。
模型的复杂度一般体现在:深度大小和也节点数量,深度小且叶节点少则模型简单,深度大且叶节点大则模型辅助。
剪枝的目的:处理决策树的过拟合问题
剪枝的分类:预剪枝和后剪枝
预剪枝:生成过程中,对每个结点划分前进行估计,若当前结点的划分不能提升 [泛化能力] ,则停止划分,记当前结点为叶结点。
后剪枝:生成一棵完整的决策树后,从底部向上对内部结点进行考察,如果将 [内部结点变成叶结点] ,可以提升泛化能力,那么就进行交换。
预剪枝的方法:
- 限定决策树的深度
- 设定一个阈值
- 设置某个指标,比较节点划分前后的泛化能力
限定决策树的深度
输入:色泽、根蒂、敲声、纹理、脐部、触感
输出:是否好瓜
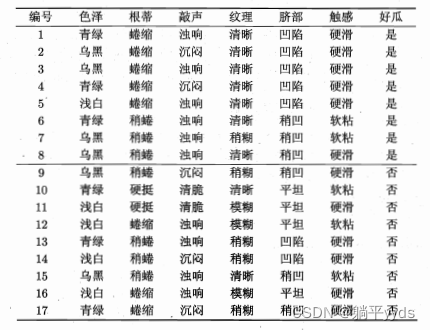
通过ID3算法中的信息增益确定决策树
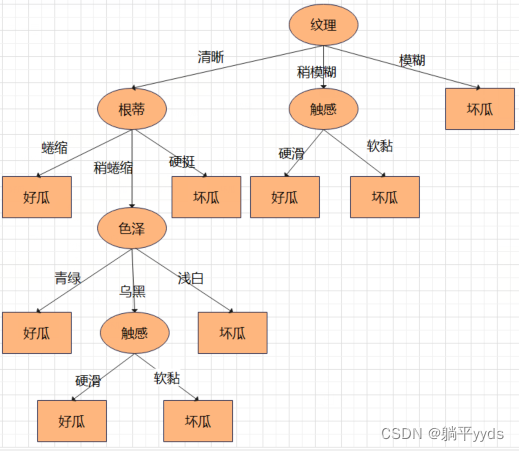
这颗树深度从0开始一共四层。现在要将深度限定为2层,也就是要在色泽节点进行剪枝,先把把符合「纹理清晰、根蒂稍蜷缩」中的数据集挑出来,就只有第6、第8、第15行符合要求。
| 编号 | 色泽 | 根蒂 | 悄声 | 纹理 | 脐部 | 触感 | 是否好瓜 |
|---|---|---|---|---|---|---|---|
| 6 | 青绿 | 稍蜷缩 | 浊响 | 清晰 | 稍凹 | 软粘 | 是 |
| 8 | 乌黑 | 稍蜷缩 | 浊响 | 清晰 | 稍凹 | 硬滑 | 是 |
| 15 | 乌黑 | 稍蜷缩 | 浊响 | 清晰 | 稍凹 | 软黏 | 否 |
在这个数据中,2个好瓜,1个坏瓜,认为替换后的叶结点标记为好瓜。
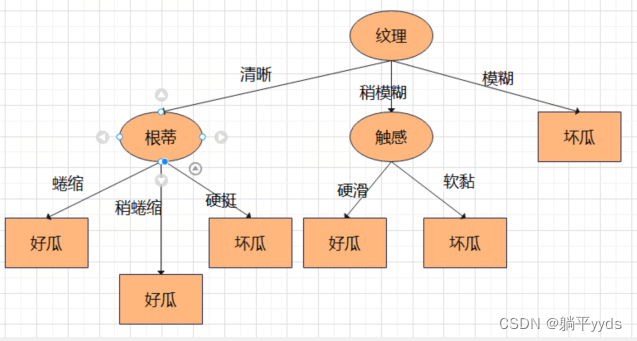
设定一个阈值
「输入」:训练数据集D,特征集A,阈值
∈
in
∈
「输出」:决策树
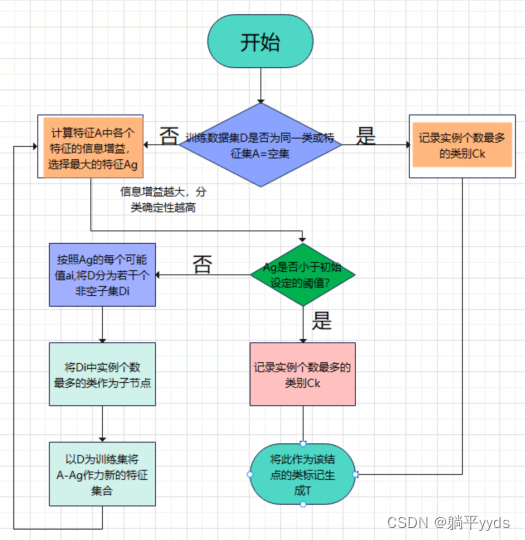
在ID3算法的话,阈值出现在信息增益的比较环节,阈值不同,生成的树也会不同,
设阈值
∈
=
0.4
in=0.4
∈=0.4 ,根据特征计算出来的信息增益都是小于阈值的,也就是说特征并不会个分类带来确定性,那么可以根据数据集中好瓜和坏瓜的数量来确定类标记填什么。
| 特征 | 信息增益 |
|---|---|
| 色泽 | 0.109 |
| 根蒂 | 0.143 |
| 敲声 | 0.141 |
| 纹理 | 0.381 |
| 脐部 | 0.289 |
| 触感 | 0.006 |
17个样本,9个坏瓜,8个好瓜,坏瓜多,则直接剪枝并认为是坏瓜,得到一颗单节点树并将其标记为坏瓜。
设置某指标,比较结点划分前后的泛化能力
测试集上的误差率:测试集中错误分类的实例占比:
测试集上的准确率:测试集中正确分类的实例占比。
误差率越高,代表泛化能力越弱,误差率越低,代表泛化能力越强
-
计算根节点处的误差率
这种方法是基于测试集上的误差率来实现的,用上面的的数据分成两部分进行预剪枝。
训练集
编号 色泽 根蒂 敲声 纹理 脐部 触感 是否好瓜 1 青绿 蜷缩 浊响 清晰 凹陷 硬滑 是 2 乌黑 蜷缩 沉闷 清晰 凹陷 硬滑 是 3 乌黑 蜷缩 浊响 清晰 凹陷 硬滑 是 6 青绿 稍蜷缩 浊响 清晰 稍凹 软粘 是 7 乌黑 稍蜷缩 浊响 稍模糊 稍凹 软粘 是 10 青绿 硬挺 清脆 清晰 平坦 软粘 否 14 浅白 稍蜷缩 沉闷 稍模糊 凹陷 硬滑 否 15 乌黑 稍蜷缩 浊响 清晰 稍凹 软粘 否 16 浅白 蜷缩 浊响 模糊 平坦 硬滑 否 17 青绿 蜷缩 沉闷 稍模糊 稍凹 硬滑 否 训练集中5个好瓜,5个坏瓜,先看一下测试集中的情况,3个好瓜,四个坏瓜
测试集
编号 色泽 根蒂 敲声 纹理 脐部 触感 是否好瓜 4 青绿 蜷缩 沉闷 清晰 凹陷 硬滑 是 5 浅白 蜷缩 浊响 清晰 凹陷 硬滑 是 8 乌黑 稍蜷缩 浊响 清晰 稍凹 硬滑 是 9 乌黑 稍蜷缩 沉闷 稍模糊 稍凹 硬滑 否 11 浅白 硬挺 清脆 模糊 平坦 硬滑 否 12 浅白 蜷缩 浊响 模糊 平坦 软粘 否 13 青绿 稍蜷缩 浊响 稍模糊 凹陷 硬滑 否 剪枝前误差率:
假如记根节点为一个内部节点,按信息增益选择最优特征生成决策树。
信息增益:
特征 条件熵 信息增益 色泽 0.724 0.276 根蒂 0.885 0.115 敲声 0.828 0.172 纹理 0.828 0.172 脐部 0.724 0.276 触感 1 0 生成的决策树:因为色泽和脐部的信息增益最大且一样,选择其中一个就可以。凹陷的瓜有3个为好瓜,1个为坏瓜,那么就认为凹陷对应好瓜啦;稍凹的瓜中,有2个是好瓜,2个是坏瓜,这里类标记不妨是好瓜;平坦的瓜中,2个都是坏瓜,得到类标记坏瓜。
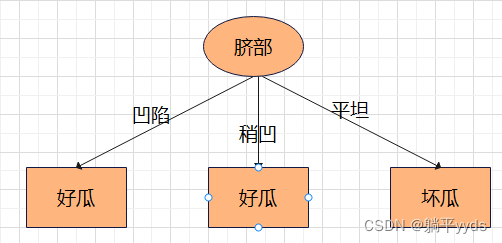
用这颗决策树对训练数据集进行判断,由上图可知脐部偶先和稍凹对应的瓜是好瓜,脐部平坦对应坏瓜,但在测试集中13和9中的结果和决策树的结果不一样,2个分类错误,所以误差率为 2 7 frac{2}{7} 72
剪枝后的误差率
若此处采取剪枝的策略,则根结点为一个叶子结点,通过训练集可以得出类标记为“好瓜”或“坏瓜”的结论,我们任选其一即可。
- 假如记为「好瓜」,那么测试集中有4个坏瓜都被误判为好瓜,得出误差率为 4 7 frac{4}{7} 74。
- 假如记为「坏瓜」,那么有3个坏瓜都被误判为好瓜,得出误差率为 3 7 frac{3}{7} 73。
发现无论叶子节点标为哪种类型,误差率都明显提高了,所以可以得出结论根结点处不剪枝。
-
计算第一层处的误差率
- 第一层第一个节点剪枝前的误差率
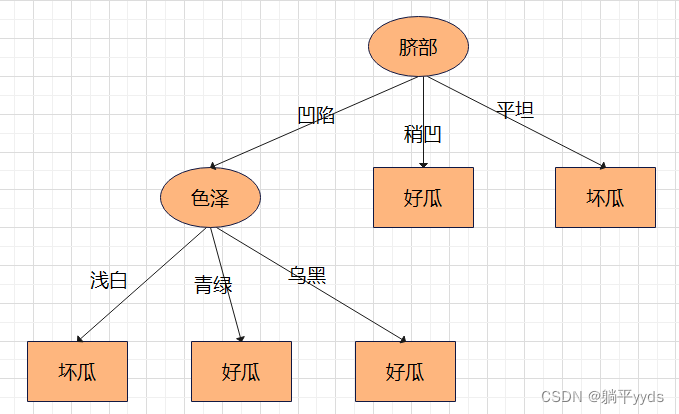
根据信息增益继续选择最优特征,最大信息增益为色泽,内部节点为色泽,计算此时测试集上误差率
3
7
frac{3}{7}
73,比较之前测试集的误差率
2
7
frac{2}{7}
72,发现误差率提高了,所以结论是第一层第一个节点处剪枝。
-
第一层第一个节点剪枝后的误差率
剪枝后的决策树如图:
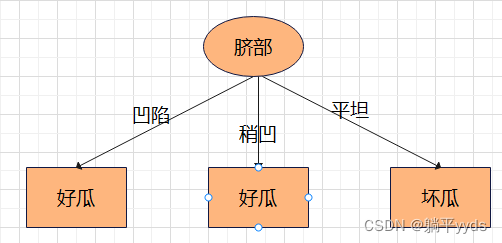
-
第一层第二个节点剪枝前的误差率
同理,根据信息增益选择最优特征,生成决策树
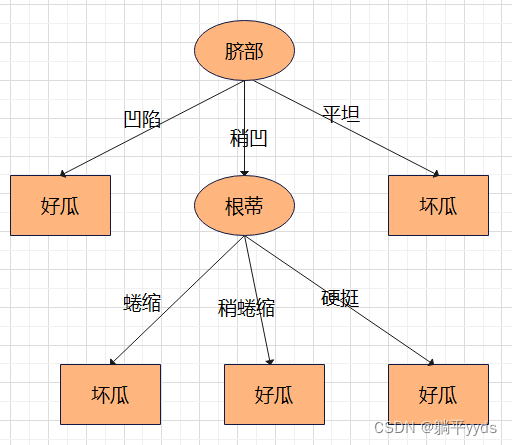
由决策树计算测试集上的误差为 2 7 frac{2}{7} 72
-
第一层第二个节点剪枝后的误差率
假如在这个节点处剪枝,根据前面的计算,测试集上误差率为 2 7 frac{2}{7} 72, 发现剪枝前后的误差率相同,对应相同的误差率,则选择深度小的决策树,所以在该节点处进行剪枝
-
第一层第三个节点
因为该节点全是坏瓜,所以不需要划分。
- 生成最终的决策树
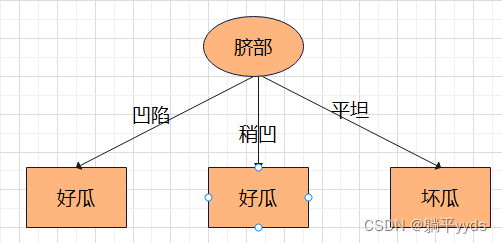
总结:预剪枝的特点是从根节点开始,一边生成决策树,一边根据上面提到的三种方法(深度、阈值、或者指标)进行剪枝。
最后
以上就是笨笨哈密瓜最近收集整理的关于决策树的预剪枝的全部内容,更多相关决策树内容请搜索靠谱客的其他文章。








发表评论 取消回复