数值线性代数Jacobi迭代法解线性方程组MATLAB实现

算法思想

如何利用电子计算机来快速、有效地求解线性方程组是数值线性代数研究的核心问题，而且也是目前人在继续研究的重大课题之一。
考虑非奇异的线性代数方程组Ax=b，令A=D-L-U，其中D=diag(diag(A))，L=-tril(A,-1)，U=-triu(A,1)。
即D对角线与A相同，其余都为0；L对角以下的元素与A的对应位置的元素的相反数相同，U则是对角以上。
Ax=b可以写为x=Bx+g，其中B=D^-1(L+U),g=D^-1b。通过迭代x_k=Bx_k-1+g来求解，称为Jacobi迭代法。
其中B叫做Jacobi迭代法的迭代矩阵，g叫做Jacobi迭代法的常数项。

矩阵创建

function [A,b]=creatMaxtrix(n)
    T=zeros(n-1,n-1);
    for i=1:n-1
        T(i,i)=2;
    end
    for i=1:n-2
        T(i,i+1)=-1;
        T(i+1,i)=-1;
    end
    I=eye(n-1,n-1);
    k=(n-1)^2;
    A=zeros(k,k);
    b=ones(k,1);
    j=1;
    for i=1:n-1
        A(j:j+n-2,j:j+n-2)=T+2*I;
        j=j+n-1;
    end
    j=1;
    for i=1:n-2
        A(j:j+n-2,j+n-1:j+2*n-3)=-I;
        A(j+n-1:j+2*n-3,j:j+n-2)=-I;
        j=j+n-1;
    end
end

该矩阵是一个(n-1)² 阶的矩阵，其具有这样几个特点，
(1)A是块三对角阵，共有五条对角线上有非零元素；
(2)A是不可约对角占优的；
(3)A是对称正定的，而且是稀疏的。
矩阵的形式如下

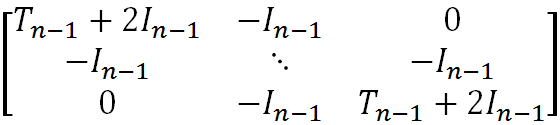
可通过spy来观察矩阵的分布，一个n=11时的矩阵分布情况如下

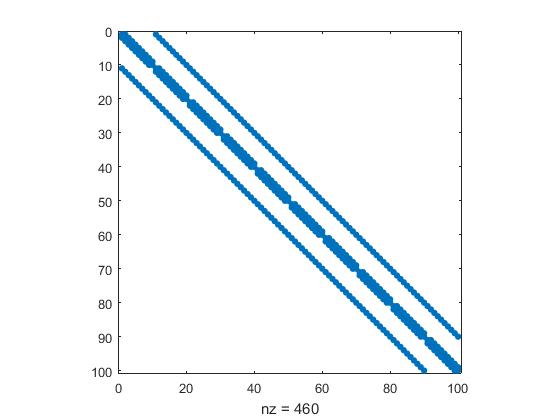
Jacobi迭代

function []=Jacobi(n,eps)
[A,b]=creatMaxtrix(n);
D=diag(diag(A));    %对角
L=-tril(A,-1);      %下三角
U=-triu(A,1);       %上三角
x=zeros((n-1)^2,1); %初始迭代点为0
k=0;                %迭代指标
maxit=20000;        %最大迭代次数  
B=D(L+U);          %迭代矩阵
g=Db;              %迭代常数项
tic
while 1
    k=k+1;
    x=B*x+g;
    %fprintf('第%d次迭代n',k);
    res=b-A*x;
    if norm(res,2)<eps
        break
    elseif k>=maxit
        fprintf('达到最大迭代次数n');
        break
    else
        continue;
    end
end
toc

总结

运行结果如下

>> Jacobi(21,1e-6)
时间已过 0.071448 秒。

为了省略篇幅，我将迭代步数注释了。此时可以明白的是算法的解与精确解之间的二范数小于10^-6。在可以控制精度的条件下，时间成了一个更重要的问题。不同迭代算法的复杂度不同，在应对实际问题时候的表现也就不同。

最后

以上就是还单身蜜粉为你收集整理的数值线性代数Jacobi迭代法解线性方程组MATLAB实现的全部内容，希望文章能够帮你解决数值线性代数Jacobi迭代法解线性方程组MATLAB实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。