matlab中欠定方程组超定方程组_第6章 解线性方程组的迭代法(基于MATLAB)

前面我们已经知道对于线性方程组，一般有两种数值解法：直接法和迭代法。直接法前面已经写过了，没看的同学可以移步阅读：直接法。本次主要讲述迭代法及其相应的MATLAB代码。

考虑线性方程组

当

为低阶稠密阵时一般采取直接法进行求解。但是我们在工程技术中经常遇到的是一些大型稀疏矩阵方程组(

的阶数很大，但

元素较多，解PDE(Partial Differential Equation)时常遇到)，此时利用迭代法进行求解是合适的。在计算机内存和运算两方面，迭代法通常都可利用

中有大量

元素的特点。

本文主要介绍迭代法的基本思路和雅可比(Jacobi)迭代法、高斯-塞德尔(Gauss-Seidel)迭代法、(逐次)超松弛(SOR, Successie over Relaxation)迭代法、共轭梯度(CG, Conjugate Gradient)法。

1. 迭代法的基本思路

对于线性方程组

为了使用迭代法对其进行求解，我们首先需要构造迭代序列，我们将上式改写为

其中

和

都是已知的，从而我们就可以构造出一个迭代序列为

对向量序列

一组初始值

，如果上述迭代序列收敛(有课本定理知其充要条件为

)，最终向量序列

将逐步逼近原方程组的精确解

。迭代次数越多，计算误差就越小，因此，任意给定一个精度，都可以通过迭代计算出满足精度要求的解(理论上，实际情况还需考虑计算机存储字长)。

这就是我们构造迭代法的基本思路。MATLAB代码为

function

示例：

clear

运行结果

x 

可见只是迭代

次，就满足默认精度(

)。

2. 雅可比(Jacobi)迭代法

其实上面第1节的代码使用的方法就是最原始的雅可比迭代法，只是在形式上看起来不那么规范。下面我们来看规范的解

的雅可比迭代法的形式：

其中

，

，这里

分别为对角阵、下三角阵、上三角阵。并称

为解

的雅可比迭代法的迭代矩阵。

其分量计算公式为

但实际编程计算一般采取简洁且高效的矩阵形式，其MATLAB代码为

function

仍然计算第一节的例子，只需把函数名改一下：

clear

运行结果也与第1节一致：

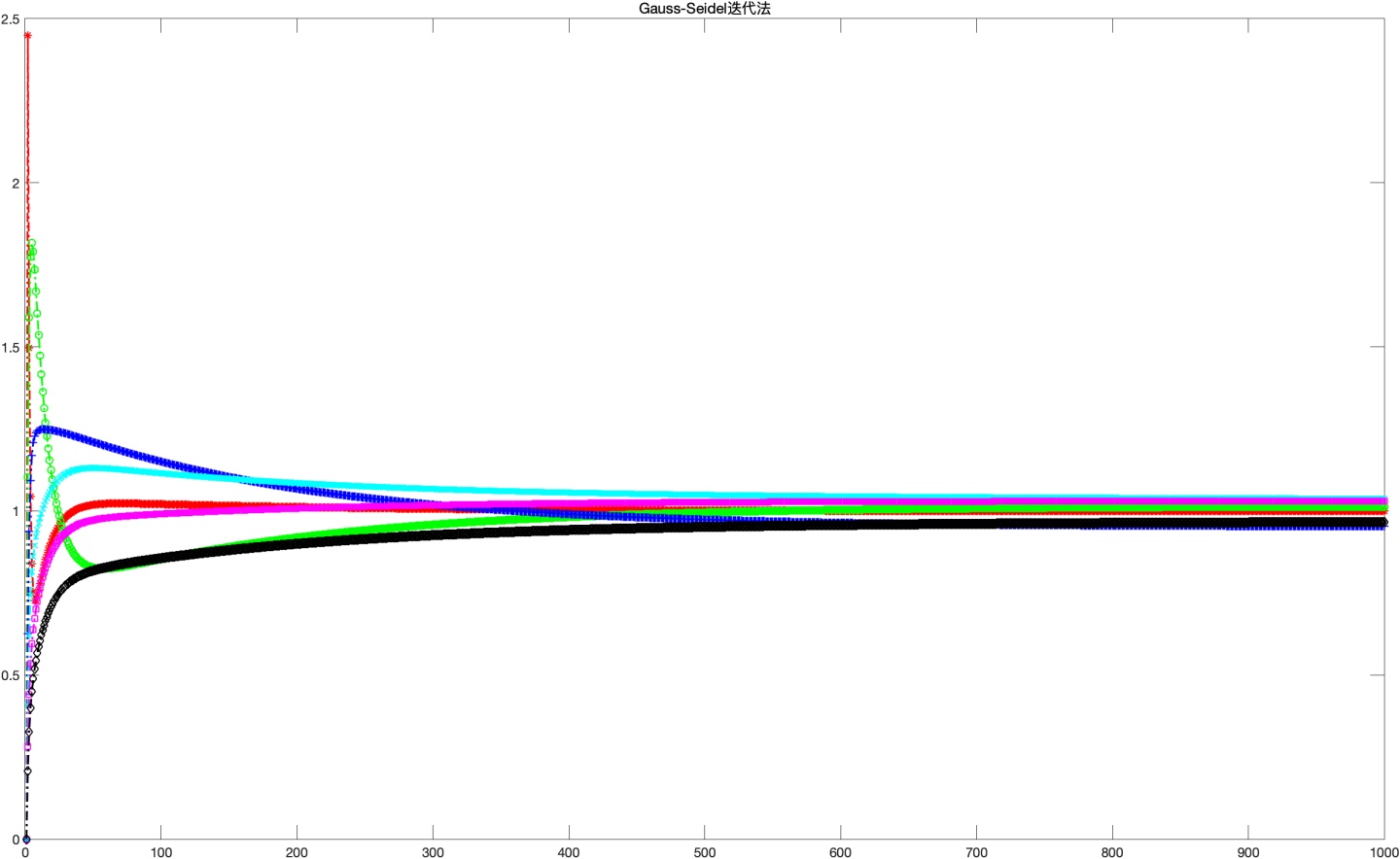
x 

3. 高斯-塞德尔(Gauss-Seidel)迭代法

高斯-塞德尔迭代法与雅可比迭代法很相似，可以看成是其的一种改进。其形式为：

其中

，

，这里

分别为对角阵、下三角阵、上三角阵。并称

为解

的高斯-塞德尔迭代法的迭代矩阵。

其分量计算公式为

其MATLAB代码亦采取矩阵形式：

function

同样计算前面的例子，其结果为：

x 

从结果可以看出，对于同样的精度要求，高斯-塞德尔迭代法只需要

次迭代(雅可比迭代法需要

次)，收敛明显要更快。

3. (逐次)超松弛(SOR)迭代法

简单来说，逐次超松弛迭代法就是在前面高斯-塞德尔迭代法的基础上加了松弛因子

，所以解

的SOR方法为

，初始向量，

其中

，

。

其分量计算公式为

显然，当

时，SOR方法即为高斯-塞德尔迭代法。当

时，称为

时，称为

其MATLAB代码为

function

还是计算前面那个例子，选择精度为

，松弛因子

：

clear

运行结果为

x 

如果采取默认松弛因子(自动选择最佳松弛因子)：

clear

其结果为

x 

此时迭代次数减少为

次，松弛因子也选择为接近

的数，与高斯-塞德尔迭代法效果基本一致。

4. 共轭梯度(CG)法

也称共轭斜量法，它是一种变分方法，对应于求一个二次函数的极值。CG方法是一种求解大型稀疏对称正定方程组十分有效的方法。

其算法描述为：

（1）任取

，计算

，取

。

（2）对

，计算

（3）若

，或

，计算停止，则

。由于

正定，故当

时，

，而

，也即

。

写成MATLAB代码为

function

用此CG方法求解一个

阶Hilbert矩阵：

clear

运行结果为：

x 

而如果采用Gauss-Seidel迭代法，精度要求为

，其结果为

x 

对比结果可以发现，达到类似精度，G-S迭代法需要迭代

次迭代，是CG方法的近

倍，足以见得在处理大型稀疏正定矩阵时CG方法的优势之明显。