1. 迭代法的基本概念

前一章讲述了线性代数方程组的直接解法，本质上还是矩阵运算，只是用了一些技巧让计算简单（在计算复杂度上可能并没有改善）。而本章讲述的是线性方程组的迭代解法，从一个初始解出发，迭代求解，逐渐收敛到目标真解。

1.1 向量序列和矩阵序列的极限

1. 向量序列的极限是根据向量中每个元素的极限来定义的，如果向量中每个元素的序列都收敛，那么向量序列收敛。
   向量序列的极限还可以根据向量范数（注意是任意向量范数，不一定要是二范数）收敛到0来定义，即：

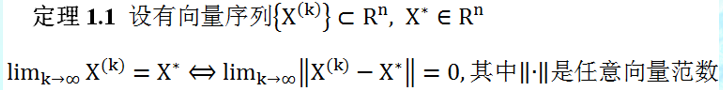
2. 矩阵序列的极限是根据矩阵中每个元素的极限来定义的，如果矩阵中每个元素的序列都收敛，那么矩阵序列收敛。
   矩阵序列的极限还可以根据矩阵范数（注意是任意矩阵范数，不一定要是二范数）收敛到0来定义，即：

3. 矩阵收敛和向量收敛的关系：

上式本质上说明了如果矩阵序列$A^{(k)}$收敛到矩阵$A$，那么向量$A^{(k)}x$会收敛到向量$Ax$

4. 下面讨论一种与迭代法有关的矩阵序列的收敛性,这种序列由矩阵的幂构成,即 { B k } {B^k} {Bk}.
   一个矩阵$B$的k次方收敛到0等价于它的谱半径小于1，即：

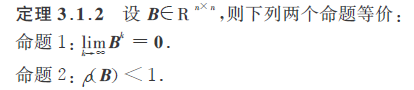
此外还有两种重要的定理：

1.2 迭代公式的构造

对于线性方程组：
$$Ax=b$$

可以用迭代方式求解，即将非奇异矩阵$A$拆解：
$$A=M-N$$
接着：

因此上式就是 迭代公式，重新整理一下记号就得：

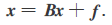
可以构造解此方程组的迭代法:

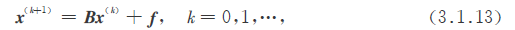
其中矩阵B称为 迭代矩阵.

迭代法何时收敛？

上式实际上是说解向量序列是收敛的，那么同样地，只要将上式移项，然后收敛到0向量，也是一个意思。通过上面的定义，可以证明如下定理：

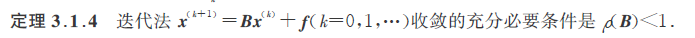
如何评价收敛的速度？

显然，矩阵的谱半径越小，收敛速度越快。

2. Jacobi迭代法和Gauss-Seidel迭代法

2.1 Jacobi迭代法

此迭代法思路很简单，将系数矩阵A拆解成 对角线元素为0的上三角矩阵，对角矩阵， 对角线元素为0的下三角矩阵。然后将对角矩阵保留在等式左边，两个三角矩阵移到等式右边，再求逆即可。即：

值得注意的是，矩阵$B_J$是完全可以口算的，即：系数矩阵对角线元素变为0，然后矩阵所有元素取相反数，最后每一行除以对角元素。

2.2 Gauss-Seidel迭代法

我们先看Jacobi迭代法：

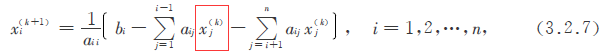
如果把上面那一项$x_j^{(k)}$换成$x_j^{(k+1)}$，就得到了Gauss-Seidel迭代法：

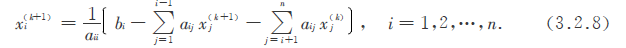
那么写成矩阵形式就是：

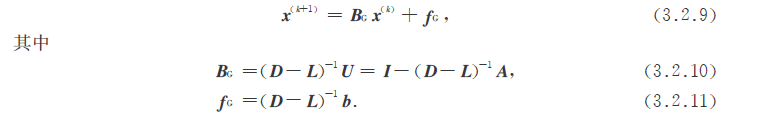
2.3 J法和GS法的收敛性

有四条判别定理：

3. 超松弛迭代法

3.1 逐次超松弛迭代公式

GS法比J法好，因为它每次迭代能用最新的值总是用最新的值$x_j^{(k+1)}$。但是将GS法做进一步推广，可以进一步加快收敛速度。

可以看到，迭代思路就是，用GS法的解和上一次的迭代解做一个线性组合，达到“中庸”的效果，进一步整理

可以看到GS法就是SOR法的一种特例。

用矩阵表示：

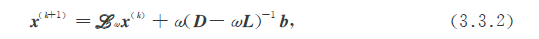
其中：

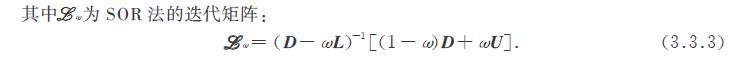
3.2 SOR迭代法的收敛性

由第二节的理论可知，SOR迭代法收敛的充分必要条件是$\rho (L_w)<1$，其中矩阵$L_w$就是式（3.3.3）所示的形式。

对于矩阵$L_w$的谱半径，有如下定理：

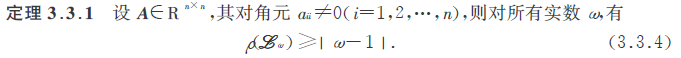
那么，如果 SOR迭代法收敛 则有：$|w-1|<1$，因此：$0<w<2$是收敛的 必要条件，如果这个条件不满足，SOR迭代法必定不收敛。

以下定理是关于$0<w<2$与SOR收敛关系的一个充分必要条件。

3.3 最优松弛因子

SOR迭代法的收敛速度与谱半径有关，而谱半径又与松弛因子$w$有关.我们希望选取最优的松弛因子$w$,使得迭代矩阵谱半径最小，即收敛速度最快。

对于一个矩阵$A$，如果满足 对称、正定、三对角，那么它有如下三条性质：

如果矩阵满足 对称、正定、三对角，那么$\rho (L_w)$作为$w$的函数，其图形如下所示：

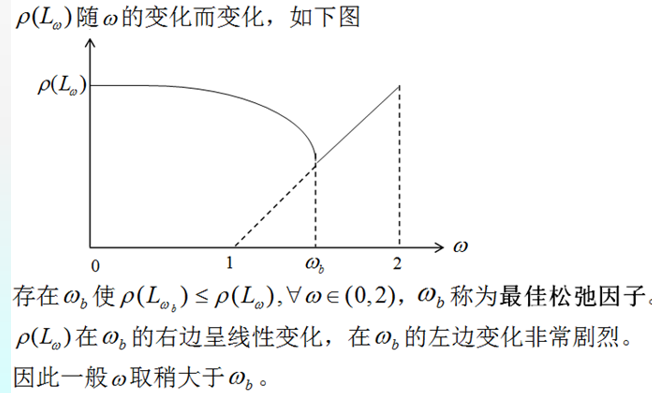
参考文献：
关治，陆金甫《数值方法》

最后

以上就是健康面包为你收集整理的数值分析(3)：线性代数方程组的迭代解法1. 迭代法的基本概念2. Jacobi迭代法和Gauss-Seidel迭代法3. 超松弛迭代法的全部内容，希望文章能够帮你解决数值分析(3)：线性代数方程组的迭代解法1. 迭代法的基本概念2. Jacobi迭代法和Gauss-Seidel迭代法3. 超松弛迭代法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。