线性代数方程组的解法

一、实验要求

分别采取Guass消元法（不选主元、手动选主元、自动选主元）、Jacobi迭代法、Guass-Seidel迭代法、超松弛迭代法计算下列矩阵的线性方程组。
（1）矩阵A=$\left[\begin{array}{ccccc}6& 1& & & \\ 8& 6& 1& & \\ & \dots & \ddots & \ddots & \\ & & 8& 6& 1\\ & & & 8& 6\end{array}\right]$，b=$\left[\begin{array}{c}7\\ 15\\ ⋮\\ 15\\ 14\end{array}\right]$
（2）希尔伯特矩阵

（3）其他矩阵

二、实验过程

实验成果

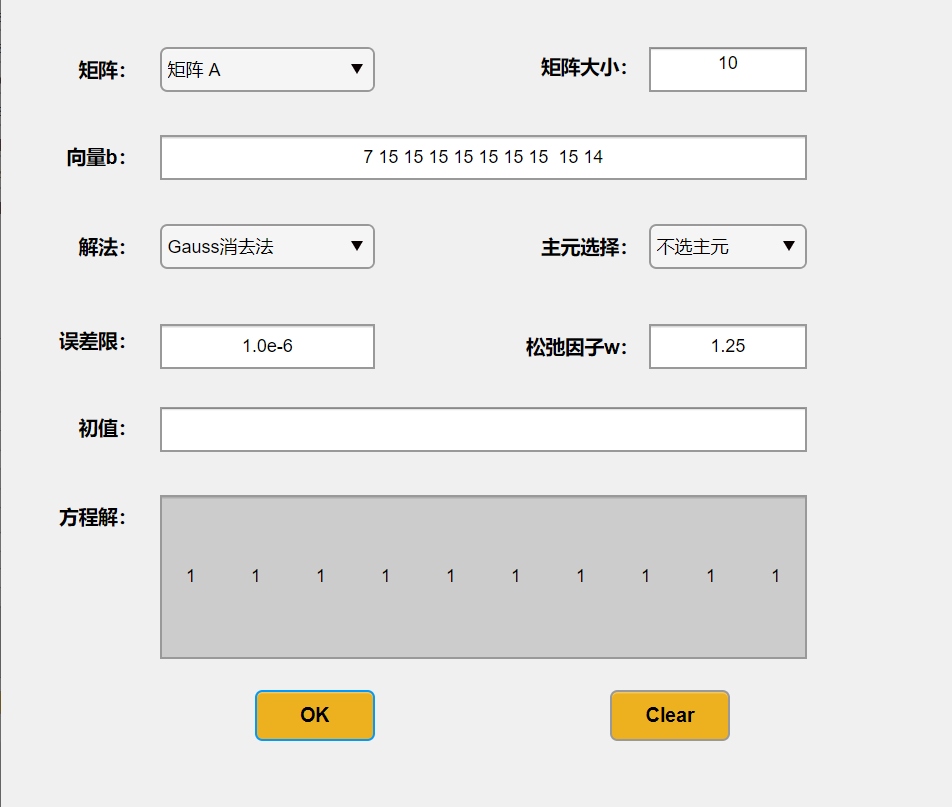
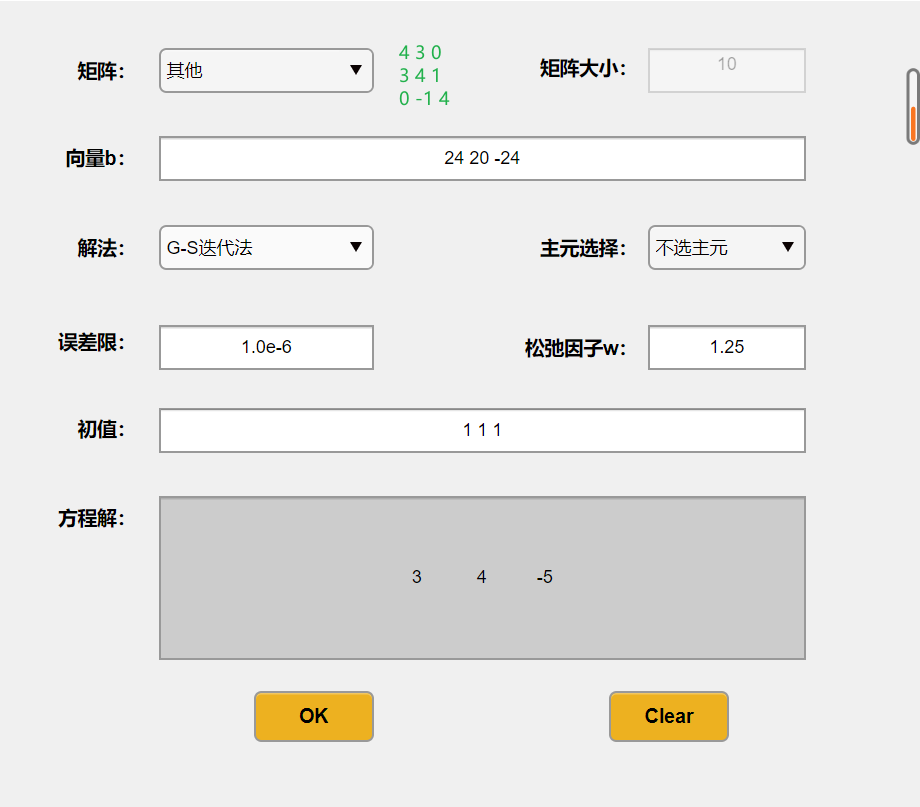
主程序

1、Guass消去法主元选择函数（不选主元、手动选主元、自动选主元）和Jacobi迭代法、Guass-Seidel迭代法、超松弛迭代法的函数

   methods (Access = private)
        
        %主元选择所需要的函数
        function [m,l] = mymax(app,x)
            %获取数列x中绝对值最大的值及其下标
            m=x(1);
            l=1;
            n=length(x);
            for i =2:n
                if abs(x(i))>abs(m)
                    m=x(i);
                    l=i;
                end
            end
        end
        
        function B=zhuxuanxq(app,A,value)
            %主元选取（自动，手动，不选）
            [row,col ]=size(A);
            if value=='自动选主元'
                [m,L]=mymax(app,A(1:row));
            elseif value=='不选主元'
                m=A(1);
                L=1;
            elseif value=='手动选主元'
                A1=A(1:row);
                L=str2num(char(inputdlg('请输入最大主元所在的行：')));
                m=A1(L);
            end
            if m==0
                return
            end
            B=A;
            B(1,:)=A(L,:);
            B(L,:)=A(1,:);
            for x =2:row
                B(x,:)=B(x,:)-B(1,:)*B(x,1)/m;
            end
        end
        
        function B=zhuxuanbh(app,A,value)
            %主元选取变换
            [row,col]=size(A);
            B=zeros(row,col);
            for i = 1:row-1
                B(i:row,i:col)=zhuxuanxq(app,A,value);
                A=B(i+1:row,i+1:col);
            end
        end
        
        %计算方法选择
        function y=jacobi(app,A,b,x0,tol)
            % Jacobi迭代法
            D=diag(diag(A));
            L=tril(A,-1);
            U=triu(A,1);
            B=-D(L+U);
            F=Db';
            x0=x0';
            y=B*x0+F;
            n=1;
            while norm(y-x0)>=tol
                x0=y;
                y=B*x0+F;
                n=n+1;
            end
        end
        
        function y=guass_seidel(app,A,b,x0,tol)
            % guass_seidel迭代
            D=diag(diag(A));
            L=tril(A,-1);
            U=triu(A,1);
            G=-(D+L)U;
            F=(D+L)b';
            x0=x0';
            y=G*x0+F;
            n=1;
            while norm(y-x0)>=tol
                x0=y;
                y=G*x0+F;
                n=n+1;
            end
        end
        
        function y=sor(app,A,b,w,x0,tol)
            %超松弛迭代
            D=diag(diag(A));
            L=tril(A,-1);
            U=triu(A,1);
            lw=(D+w*L)((1-w)*D-w*U);
            F=(D+w*L)b'*w;
            x0=x0';
            y=lw*x0+F;
            n=1;
            while norm(y-x0)>=tol
                x0=y;
                y=lw*x0+F;
                n=n+1;
            end
        end
    end

2、【矩阵】下拉框

            global A;
            Nb = string(app.DropDown.Value);
            n=str2num(char(app.TextArea.Value));
            if Nb=='矩阵 A'
                a1=sparse(1:n,1:n,6);
                a2=sparse(1:n-1,2:n,1,n,n);
                A=a1+a2+8*a2';
                app.bEditField.Value = '7 15 15 15 15 15 15 15  15 14';
            elseif Nb=='矩阵 H'
                A=hilb(n);
            elseif Nb=='其他'
                Ans=inputdlg('请输入矩阵A：','text_6',3);
                A=str2num(Ans{1});
                app.TextArea.Enable='off';   
            end

3、【解法】下拉框

            if string(app.DropDown_2.Value)=='Gauss消去法'
                app.EditField.Enable='off';
                app.wEditField.Enable='off';
            else
                app.EditField.Enable='on';
                app.wEditField.Enable='on';
            end

4、【OK】按钮

            value=string(app.DropDown_3.Value);
            b=str2num(char(app.bEditField.Value));
            global A;
            if string(app.DropDown_2.Value)=='Gauss消去法'
                B=zhuxuanbh(app,[A b'],value);
                [row ,col]=size(B);
                X=zeros(row,1);
                X(row)=B(row,col)/B(row,row);
                for k = row-1:-1:1
                    X(k)=(B(k,col)-B(k,k+1:row)*X(k+1:row))/B(k,k);
                end
            else
                tol=str2num(char(app.EditField.Value));
                x0=str2num(char(app.EditField_3.Value));
                w=str2num(char(app.wEditField.Value));
                if isempty(x0)
                    errordlg('请输入初值x0')
                    return
                end
                if string(app.DropDown_2.Value)=='Jacobi迭代法'
                    X=jacobi(app,A,b,x0,tol);
                elseif string(app.DropDown_2.Value)=='G-S迭代法'
                    X=guass_seidel(app, A,b,x0,tol);
                elseif string(app.DropDown_2.Value)=='SOR迭代法'
                    X=sor(app,A,b,w,x0,tol);
                end
            end
            app.EditField_2.Value=num2str(X');

5、【close】按钮

            app.DropDown.Value='矩阵 A';
            app.DropDown_2.Value = 'Gauss消去法';
            app.bEditField.Value = '7 15 15 15 15 15 15 15  15 14';
            app.EditField.Enable='off';
            app.wEditField.Enable='off';
            app.EditField_3.Value='';
            app.EditField_2.Value='';

最后

以上就是细腻身影为你收集整理的MATLAB运用(5)——线性代数方程组的解法线性代数方程组的解法的全部内容，希望文章能够帮你解决MATLAB运用(5)——线性代数方程组的解法线性代数方程组的解法所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。