迭代法求解线性方程组

一、迭代法的一般形式

相关知识了解：

向量序列的收敛性：

向量序列收敛于某个向量，当且仅当该向量序列的每个元素都收敛于相应的向量的元素：

矩阵序列的收敛性：

矩阵序列收敛某个矩阵，当且仅当该矩阵序列的每个元素收敛于相应矩阵的相应元素；

————————————————————————————————————————————————————

迭代法的一般形式：

提出问题：

————————————————————————————————————————————————————

————————————————————————————————————————————————————二、雅克比迭代法

举例：

Jacobi迭代的一般形式：

————————————————————————————————————————————————————

Jacobi迭代的矩阵形式：

————————————————————————————————————————————————————————————————————————————————————————————————————————

Gauss-Seidel迭代法

举例引入：

Gauss-Seidel迭代法的一般形式：

Gauss-Seidel迭代法的矩阵形式：

————————————————————————————————————————————————————————————————————————————————————————————————————————

收敛性问题：

迭代法的谱半径：

谱半径小于或等于任意由向量范数诱导的矩阵范数：

玄学公式：

特殊系数矩阵常用的判断收敛的条件：

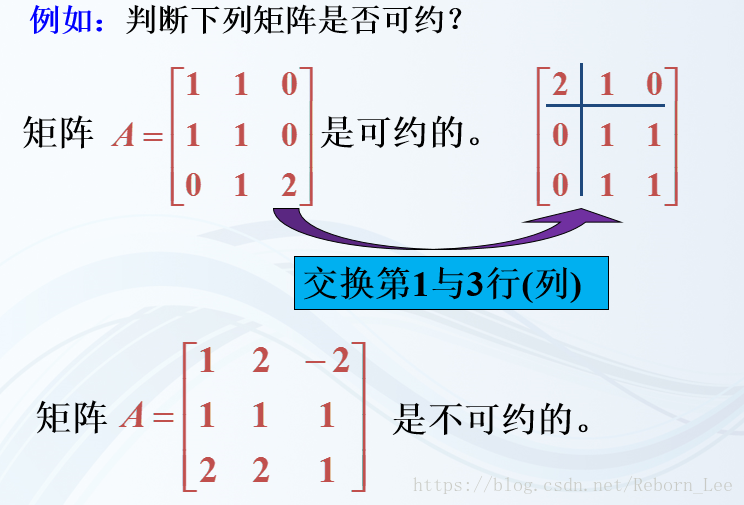
举例：

最后

以上就是成就蜻蜓最近收集整理的关于迭代法求解线性方程组的全部内容，更多相关迭代法求解线性方程组内容请搜索靠谱客的其他文章。