在学习了直接法求解线性方程组之后,我们会发现,直接法利用高斯消元法求解,计算量较大(O(n3时间复杂度))(因为高斯消元法需要将每个元素都要考虑进去)其次.无法利用矩阵的稀疏性(0元素的个数),(0其实就不用计算了)从而引出迭代法(循环计算的过程):
目录
一、迭代法的方法介绍
二、用python代码实现
1.代码实现思路(重点):
2.注意的问题
三、整体代码
四、运行结果
一、迭代法的方法介绍
1.目的:下面图片的左边是我写出的一个增广矩阵(m,b),求解:mx=b的解是多少,即:x1=?
x2=? x3=? x4=?
2.方法:先假设求出的解是 ans=[ 0, 0 , 0, 0],即初始化。然后用每一行分别依次表示出每个具体的解,即我下面图片的右边所示。
二、用python代码实现
1.代码实现思路(重点):
鉴于我在高斯消元法上面的经验(高斯消元法我个人觉得比迭代法难,我上一个博文详细介绍了高斯消元法,所以我对遍历行和列采用几个for循环比较清楚,大家如果没思路可以先看看别人的代码,然后慢慢理解,写出自己的代码),我先考虑到计算一次迭代的过程,然后在循环几次,直到达到自己的目的。下面是我迭代了100次。
for i in range(100):
print(i)
print(solution(m))接下来我们一次看一下迭代一次是如何实现的 :
迭代一次也就是说,我们需要在一次结束的时候需要将ans[]解的数组刷新一下,然后在一次的计算过程中,我们的计算顺序是从上到下、从左到右,从上到下依次遍历每一行,在每一行的数据中将非主对角线中的元素累加起来,然后赋值给一个临时变量t,然后每一行的最后一个值减去t,并且除以相对应的一行主对角线上的值,这样完成一次就会得到一个解,大家可以看看我的第一张图片中右边对每个解的表示,对比下面代码来看,比较好理解。
def solution(m):
#用来存放求出的解,设初始解为[0,0,0,0].
#这里需要
for row in range(len(m)):#按一行一行进行 0, 1, 2 3
t=0
for col in range(len(m[0])-1):#在一行中按列进行0,1,2,3 0,1,2,3
if (row!=col):
t += m[row][col]*ans[col]
ans[row]=(m[row][-1]-t)/m[row][row]
return ans
2.注意的问题
我们需要注意一个细节,对解的初始化,我没有放在定义的这个函数之中,因为初始化只需要初试一次,在接下来的迭代过程中就会用上一次计算的结果,可以看一哈我接下来的整体代码。
三、整体代码
"""
作者:author
日期:2022年09月22日
"""
import numpy as np
m= np.array([[10, -1, 2, 0, 6], [-1, 11, -1, 3, 25], [2, -1, 10,-1,-11],[0, 3, -1, 8, 15]])
print(m)
ans=[0,0,0,0]
def solution(m):
#用来存放求出的解,设初始解为[0,0,0,0].
#这里需要
for row in range(len(m)):#按一行一行进行 0, 1, 2 3
t=0
for col in range(len(m[0])-1):#在一行中按列进行0,1,2,3 0,1,2,3
if (row!=col):
t += m[row][col]*ans[col]
ans[row]=(m[row][-1]-t)/m[row][row]
return ans
for i in range(100):
print(i)
print(solution(m))
四、运行结果
下面的这一张图片是我迭代了100次的效果: 解已经出来了。
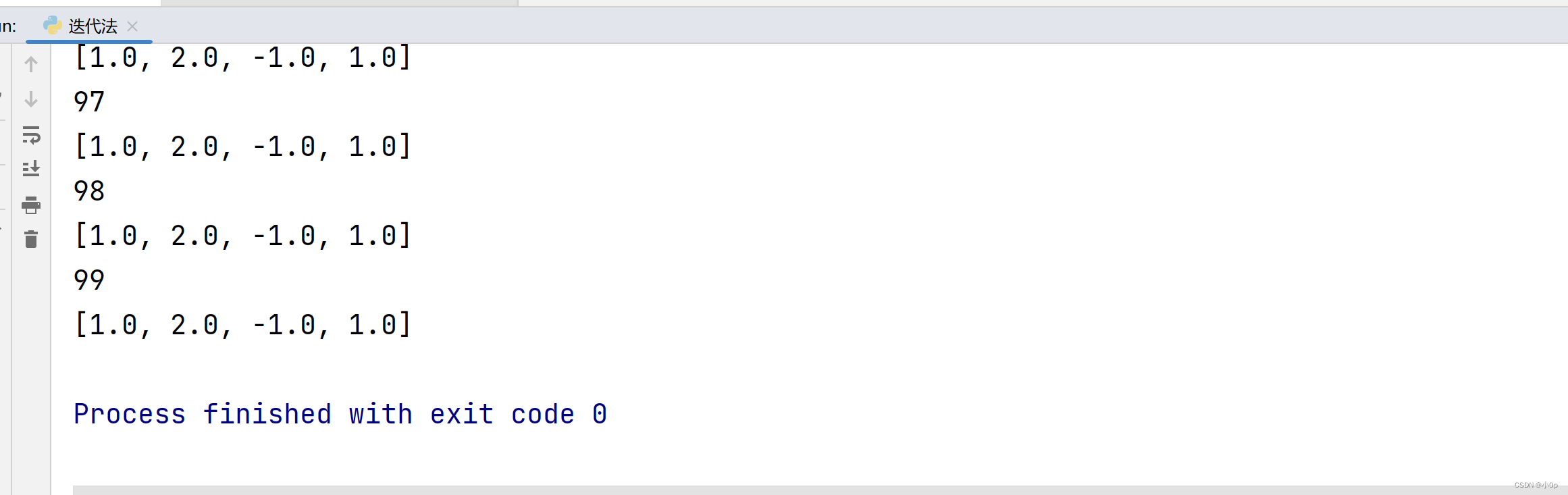
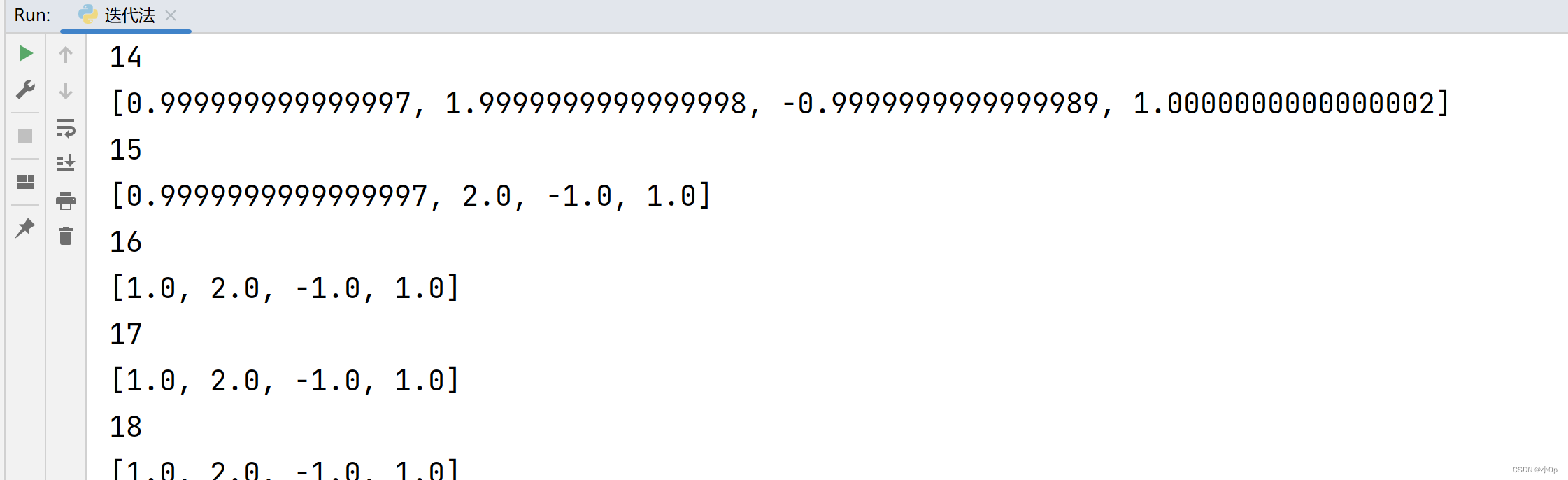
其实我们可以看到当迭代到第15次的时候,结果已经出来了。
最后谢谢大家阅读,如果觉得有帮助,可以给我点一个赞!!!你的支持是我持续更新的动力。
最后
以上就是鳗鱼鲜花最近收集整理的关于迭代法求解线性方程组(优于高斯消元法)一、迭代法的方法介绍 二、用python代码实现三、整体代码四、运行结果的全部内容,更多相关迭代法求解线性方程组(优于高斯消元法)一、迭代法内容请搜索靠谱客的其他文章。
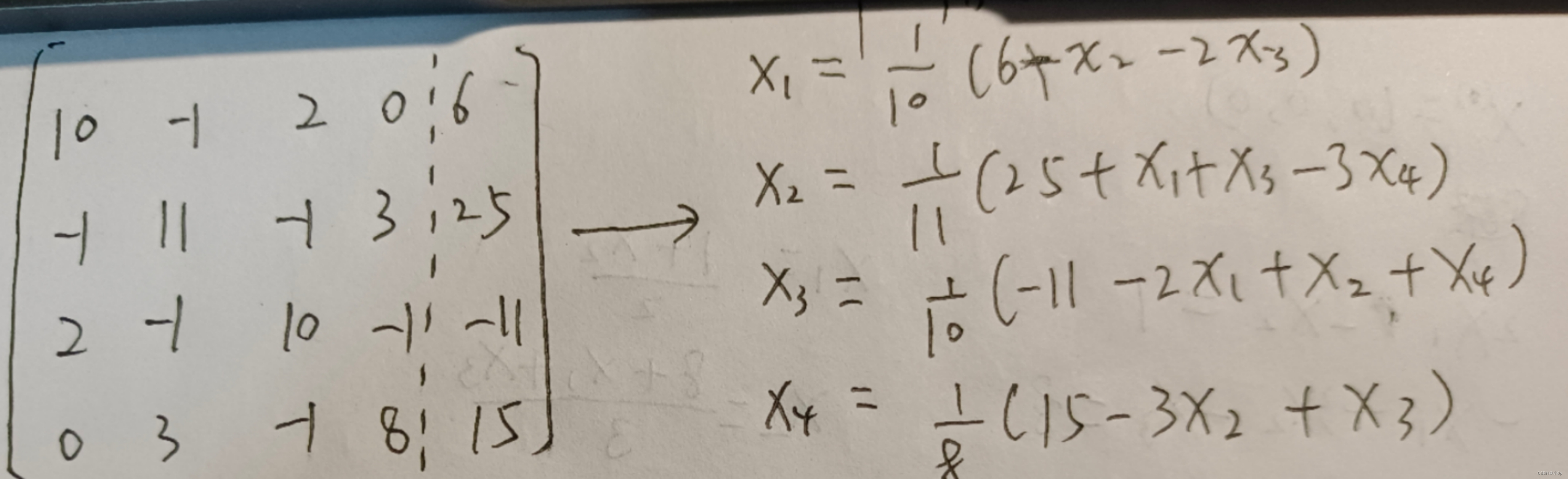








发表评论 取消回复