前言
圆柱绕流是流体力学中的一个经典问题。这是一个具有实际重要性的问题:桥墩、冷却塔等都是我们所面对的圆柱绕流的典型例子。旋涡脱落是这类结构在高雷诺数范围内流动时出现的一种重要现象,旋涡脱落的频率和旋涡振动幅值的分析在该结构设计中起着重要的作用。在本教程中,使用OpenFOAM对圆柱周围的层流进行了模拟,并对圆柱绕流的物理性质进行了评述。
模型简化
圆柱体直径为10mm,高10mm。
 图1.泄洪道简化模型
图1.泄洪道简化模型
网格划分
使用snappHexMesh工具对几何模型进行网格划分,网格为混合网格(如图3)。网格具体信息参数如下表1所示:
表1网格信息参数
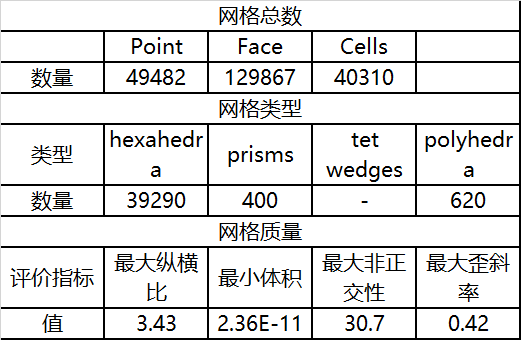

图2. 圆柱网格
物性参数
分析所涉及流场介质为空气,其相关物性参数如表2所示。
表2. 物性参数

边界条件
表3. 边界条件参数

openfoam求解器设置
本项目为求解圆柱绕流,雷诺数小于300,湍流模型选用层流laminar,需分别设置对应fvSchemes离散方法,fvSolution方程求解方法, dynamicMeshDict自适应网格配置参数及求解控制参数。
离散方法fvSchemes设置
ddtSchemes //时间离散格式,该项目瞬态计算采用欧拉离散Euler{default Euler;}gradSchemes//梯度离散,采用高斯方法,线性插值,为二阶离散{default Gauss linear;}divSchemes//散度离散,对流项采用高斯方法,线性插值,为二阶离散。divSchemes{ default none; div(phi,U) Gauss limitedLinearV 1; div(phi,S) Gauss limitedLimitedLinear 1 0 1; div(phi,nuTilda) Gauss limitedLinear 1; div((nuEff*dev2(T(grad(U))))) Gauss linear;}laplacianSchemes//拉普拉斯项离散,扩散项及压力方程离散均采用高斯理论线性插值,并带有正交修正{default Gauss linear corrected;}interpolationSchemes//插值格式,默认线性插值{default linear;}snGradSchemes//梯度法向分量,默认带有非正交修正{default corrected;}方程求解方法fvSolution设置
solvers{ "pcorr.*" { solver GAMG; tolerance 0.02; relTol 0; smoother GaussSeidel; } p { solver GAMG; tolerance 1e-06; relTol 0.01; smoother GaussSeidel; cacheAgglomeration true; nCellsInCoarsestLevel 10; agglomerator faceAreaPair; mergeLevels 1; } pFinal { solver GAMG; tolerance 1e-06; relTol 0; smoother GaussSeidel; cacheAgglomeration true; nCellsInCoarsestLevel 10; agglomerator faceAreaPair; mergeLevels 1; } U { solver smoothSolver; smoother GaussSeidel; tolerance 1e-06; relTol 0; nSweeps 1; } S { solver smoothSolver; smoother symGaussSeidel; tolerance 1e-08; relTol 0; } "(U|S)Final" { solver smoothSolver; smoother symGaussSeidel; tolerance 1e-08; relTol 0; } cellDisplacement { solver GAMG; tolerance 1e-5; relTol 0; smoother GaussSeidel; cacheAgglomeration true; nCellsInCoarsestLevel 10; agglomerator faceAreaPair; mergeLevels 1; }}PIMPLE{ correctPhi yes; nOuterCorrectors 1; nCorrectors 3; nNonOrthogonalCorrectors 0; pRefCell 0; pRefValue 0;}relaxationFactors{ fields { } equations { "U.*" 0.9; "S.*" 1; }}自适应网格参数设置
现阶段openfoam自适应网格方法只支持对六面体网格进行粗化或者细化。详细参数设置如下所示:
dynamicFvMesh dynamicRefineFvMesh;dynamicRefineFvMeshCoeffs{ // How often to refine refineInterval 1; // Field to be refinement on field S; // Refine field inbetween lower..upper lowerRefineLevel 0.01; upperRefineLevel 1; // If value < unrefineLevel unrefine unrefineLevel 10; // Have slower than 2:1 refinement nBufferLayers 2; // Refine cells only up to maxRefinement levels maxRefinement 2; // Stop refinement if maxCells reached maxCells 10000000 // Flux field and corresponding velocity field. Fluxes on changed // faces get recalculated by interpolating the velocity. Use 'none' // on surfaceScalarFields that do not need to be reinterpolated. correctFluxes ( (phi none) (phie Urel none) (phi U none) (nHatf none) (rhoPhi none) (ghf none) ); // Write the refinement level as a volScalarField dumpLevel true;}结果分析
描述圆柱绕流的最具决定性的参数是雷诺数。
在低雷诺数时,粘滞力主导流动,流动为层流,随着雷诺数的增加,粘滞力不再主导流动,流动变为紊流。对于雷诺数小于 5不存在流动分离的情况,从上游来的流体在圆柱处分流,对称地绕着圆柱的上半部和下半部流动,且不会分离。随着雷诺数的增加,在圆柱后形成了一个小的分离区域,并形成了两个相反的涡流(双涡),这些涡不会脱离,分离区域也不会向下游延伸。随着雷诺数的进一步增大,双涡在尾迹区延伸,并出现了简谐振荡。当Re大于90时,涡旋开始从圆柱的上下部分交替脱落,形成所谓的卡门涡街。在这个雷诺数范围内,尾流仍然是层流。随着雷诺数的增加(200 < Re < 300),尾迹流动变为紊流,而靠近圆柱的边界层流动仍为层流,且保持层流状态。图2.1描述了上述圆柱体周围的流动阶段。
6秒内圆柱绕流流动情况:

图3. 6秒内速度云图

图4. 6秒内流体追踪云图
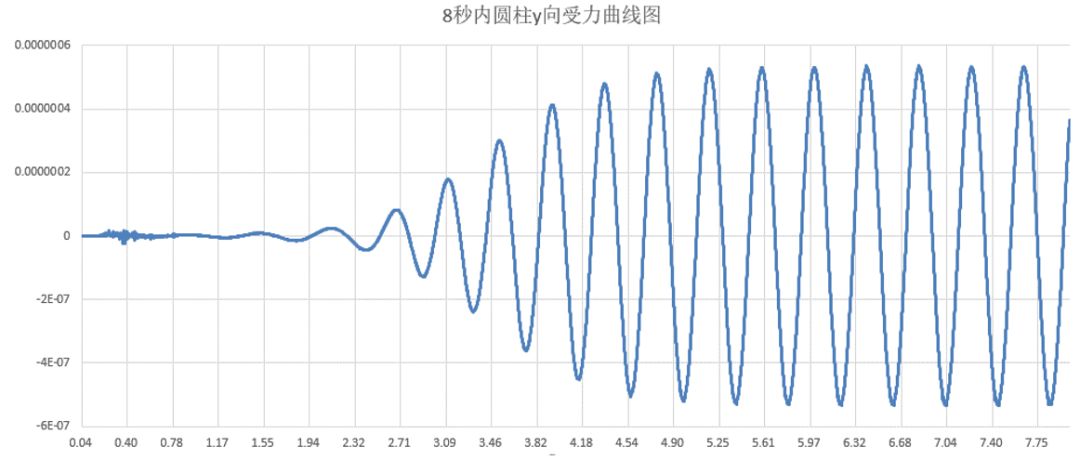
图5. 8秒内圆柱y向受力情况
各时间节点圆柱绕流流动情况:
1秒时流动情况:
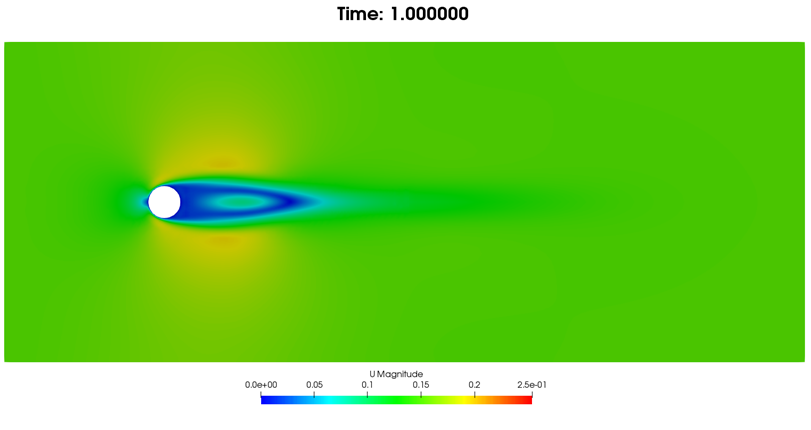
(a)速度云图
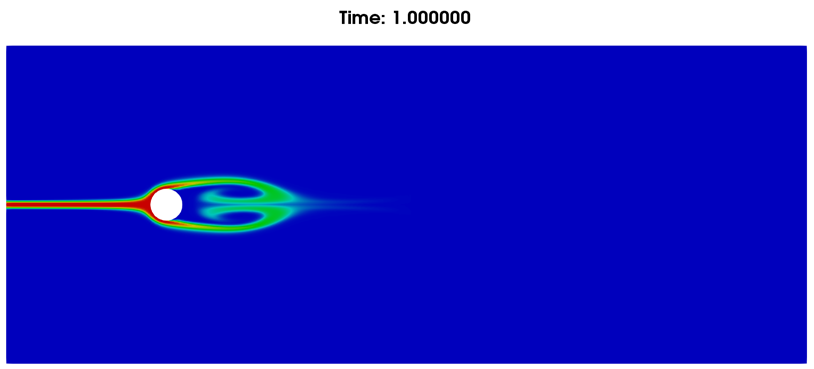
(b)流体标记追踪云图
图6. 1秒时流动情况
2秒时流动情况:
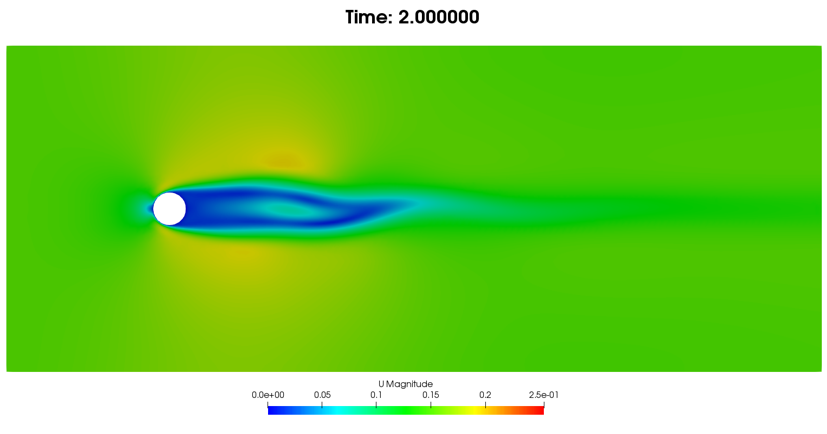
(a)速度云图
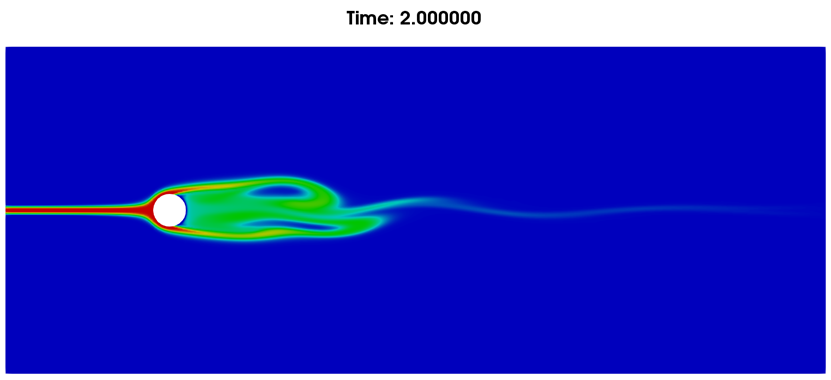
(b)流体标记追踪云图
图7. 2秒时流动情况
3秒时流动情况:
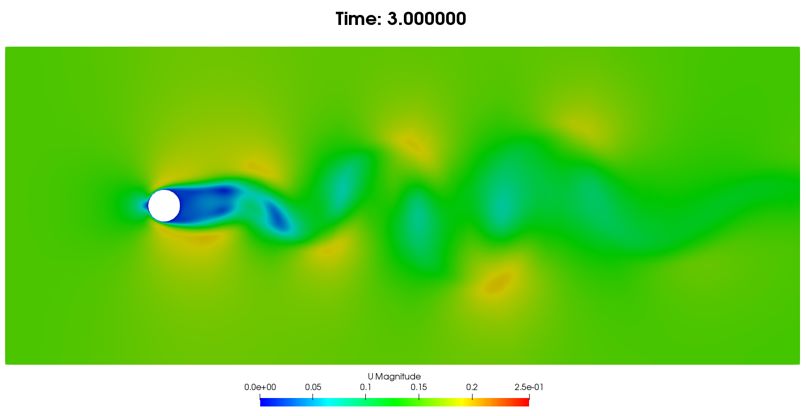
(a)速度云图
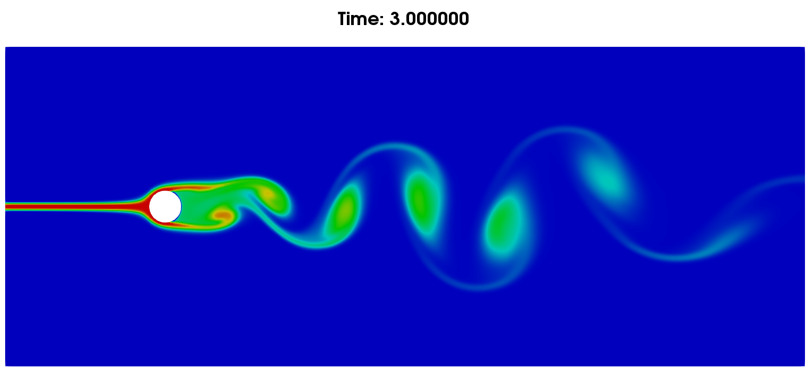
(b)流体标记追踪云图
图8. 3秒时流动情况
4秒时流动情况:
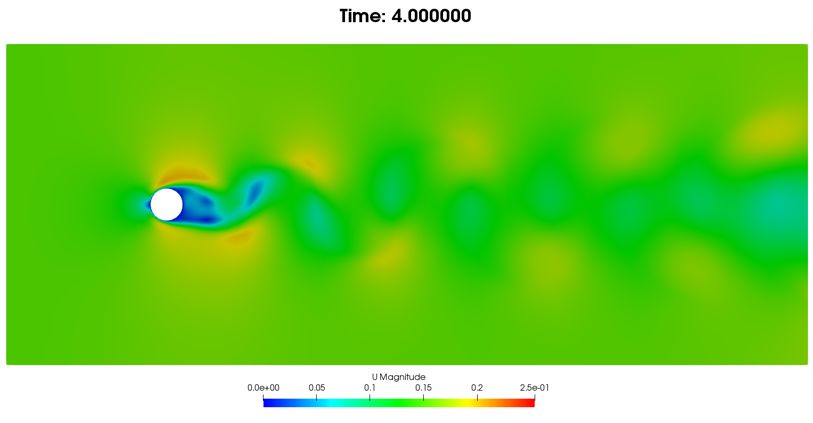
(a)速度云图
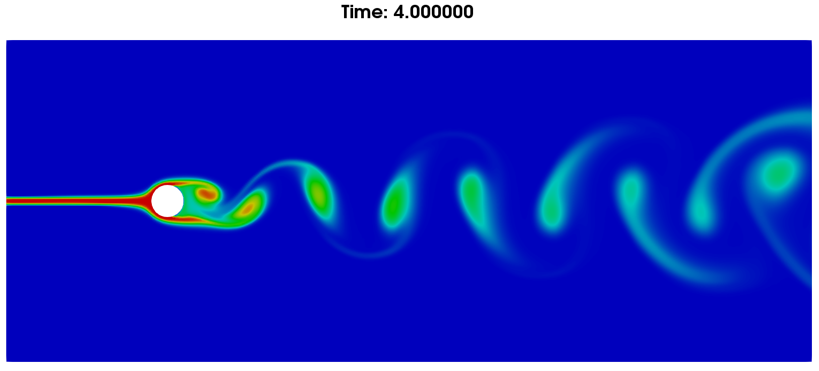
(b)流体标记追踪云图
图9. 4秒时流动情况
5秒时流动情况:
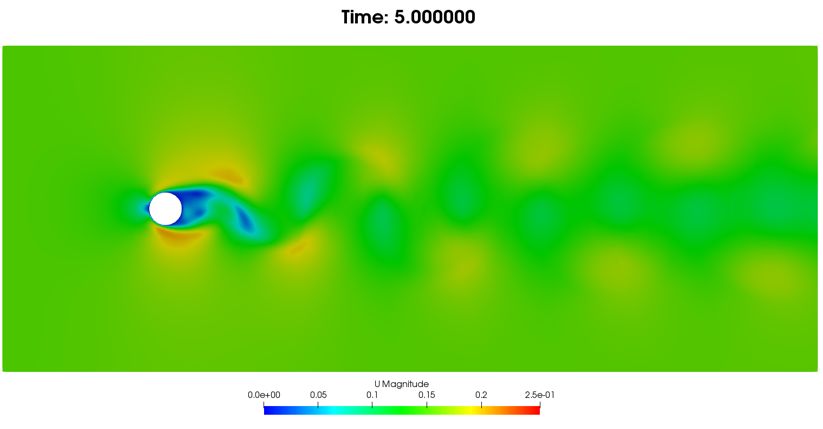
(a)速度云图
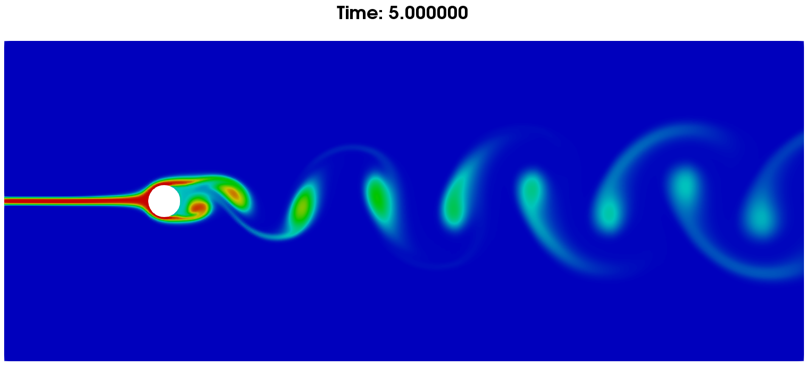
(b)流体标记追踪云图
图10. 5秒时流动情况
6秒时流动情况:
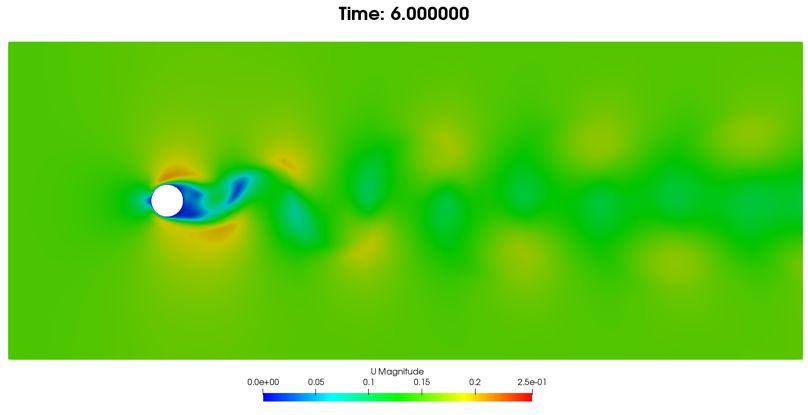
(a)速度云图
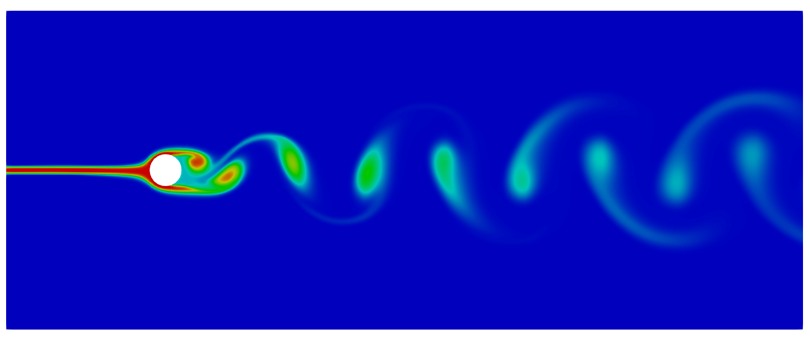
(b)流体标记追踪云图
图11. 6秒时流动情况
最后
以上就是感动曲奇最近收集整理的关于网格自适应_案例解析|基于自适应网格的圆柱绕流分析的全部内容,更多相关网格自适应_案例解析|基于自适应网格内容请搜索靠谱客的其他文章。








发表评论 取消回复