从异步十六进制加法计数器(统一使用上升沿触发的D触发器)的设计, 看异步时序逻辑电路时钟的选择

       在10.28日的博客中讲述了如何设计异步十进制加法计数器, 这里我们再以异步十六进制加法计数器的设计, 加深对异步时序逻辑电路设计思路的理解.

       设计方案1:

       第一步, 和同步时序逻辑电路的设计套路一样, 列十六进制加法计数器的状态表:

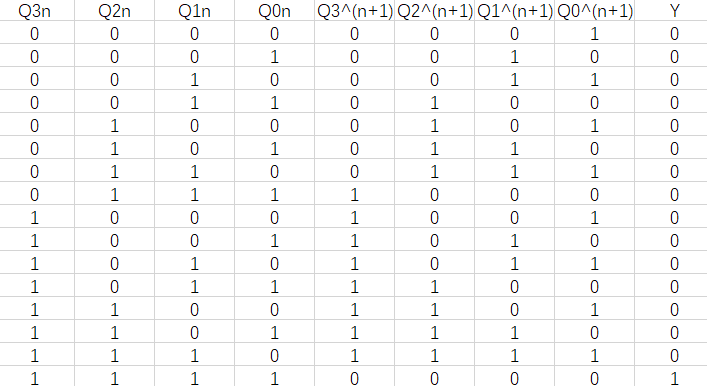
       第二步, 将状态表转换为时序图, 并从中找出Q0、Q1、Q2和Q3的变化规律:

从时序图中可以看出, 只要系统时钟迎来上升沿, Q0的状态就会变化; Q1变化在Q0的下降沿处, Q2变化在Q1的下降沿处, Q3变化在Q2的下降沿处. 根据这里的分析, 得到时钟方程 CP0=CP, CP1=Q0n', CP2=Q1n', CP3=Q2n'.

       第三步, 根据时钟方程修改状态表:

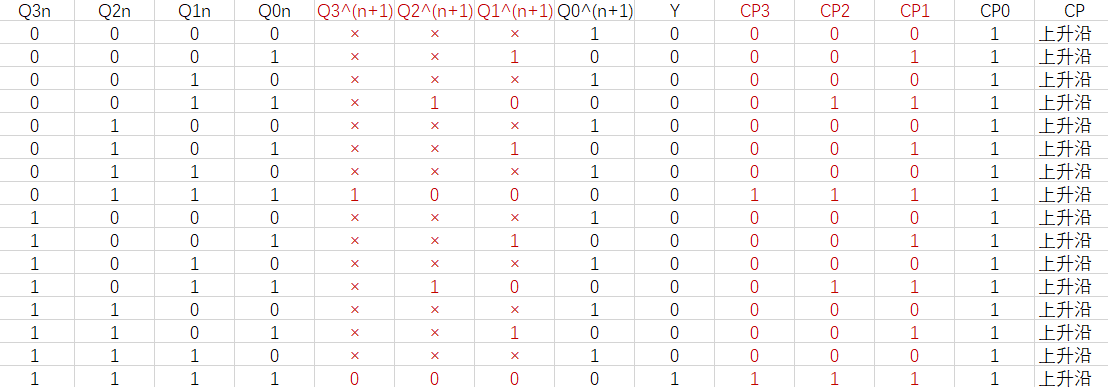
       第四步, 根据修改后的状态表, 绘制状态激励表(统一选择上升沿触发的D触发器):

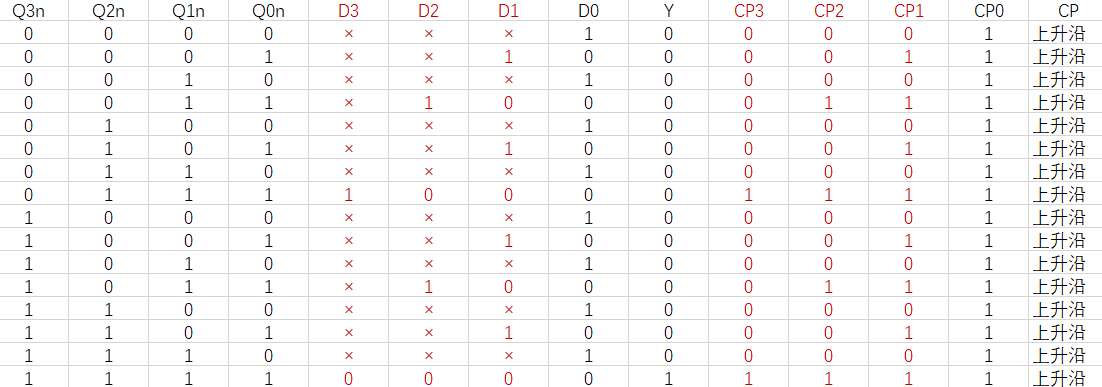
        第五步, 根据绘制的状态激励表, 求输出方程和状态激励方程:

用卡诺图化简的方式, 求得 D0=Q0n', D1=Q1n', D2=Q2n', D3=Q3n', Y=Q3n·Q2n·Q1n·Q0n.

        第六步, 求次态方程:

        Q3^(n+1)=D3=Q3n', Q2下降沿时有效;

        Q2^(n+1)=D2=Q2n', Q1下降沿时有效;

        Q1^(n+1)=D1=Q1n', Q0下降沿时有效;

        Q0^(n+1)=D0=Q0n', 系统时钟CP上升沿时有效.

        (由于电路设计采用全编码方案, 故电路不需验证自启动功能)

        第七步, 绘制电路的逻辑图:

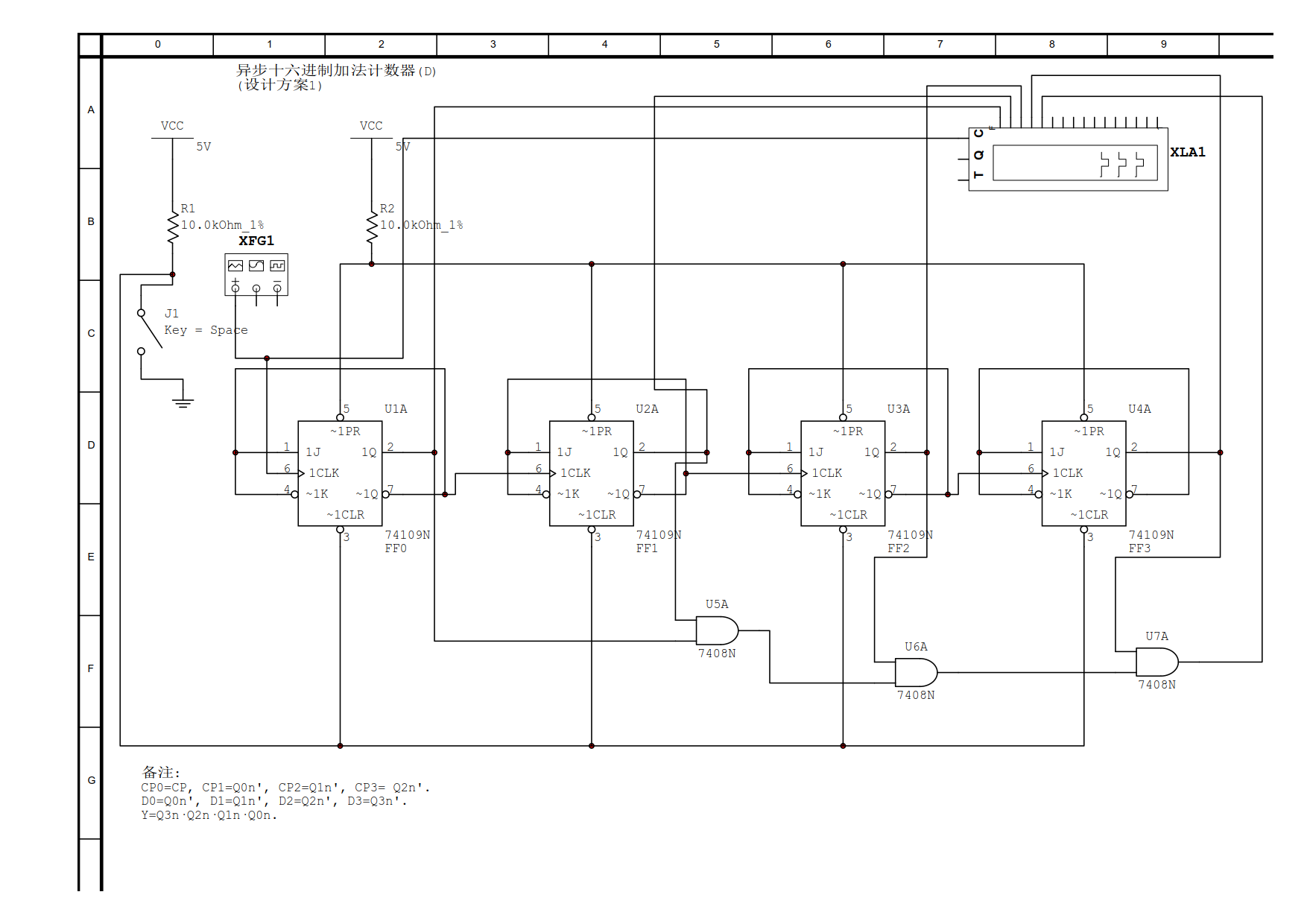
        从该电路的设计思路来看, 我们可以发现, 对异步时序逻辑电路的设计也是成体系的: 只要掌握好设计流程, 那么设计异步时序逻辑电路就不再是件难事. 

        之前我在博客中提到过, 对异步时序逻辑电路时钟的选择不是唯一的, 即还有别的选择方案. 在异步十进制加法计数器的设计描述中, 我提到了这一问题, 但没有拿出篇幅来向大家验证. 下面我将会以另一种时钟的选择对异步十六进制加法计数器进行设计.

        设计方案2:

        第一步, 列十六进制计数器的状态表:

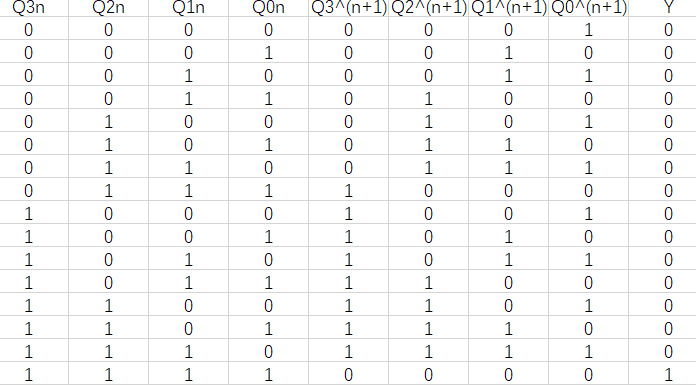
        第二步, 将状态表转换为时序图, 并从中找出Q0、Q1、Q2和Q3的变化规律:

从时序图中可以看出, Q0变化在系统时钟CP的上升沿处, Q1变化在Q0的下降沿处, Q2变化在Q0的下降沿处, Q3变化在Q0的下降沿处. 由这里的分析, 得时钟方程 CP0=CP, CP1=CP2=CP3=Q0n'.

        第三步, 根据时钟方程修改状态表:

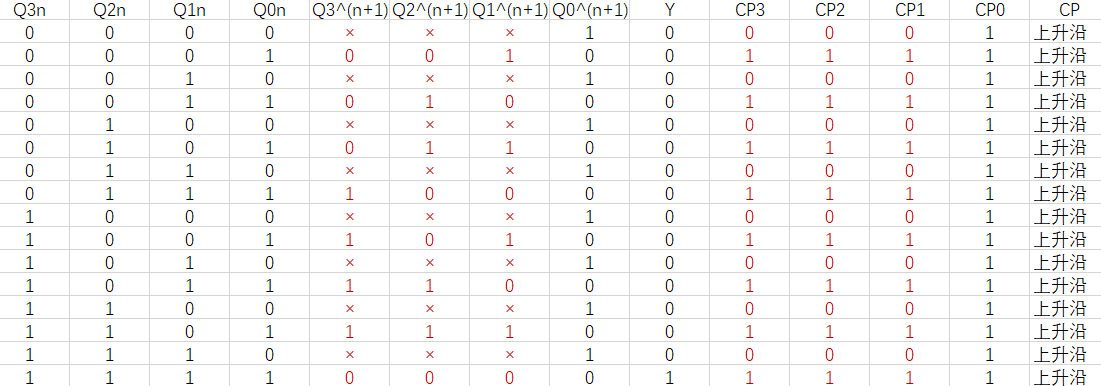
        第四步, 根据修改后的状态表绘制状态激励表:

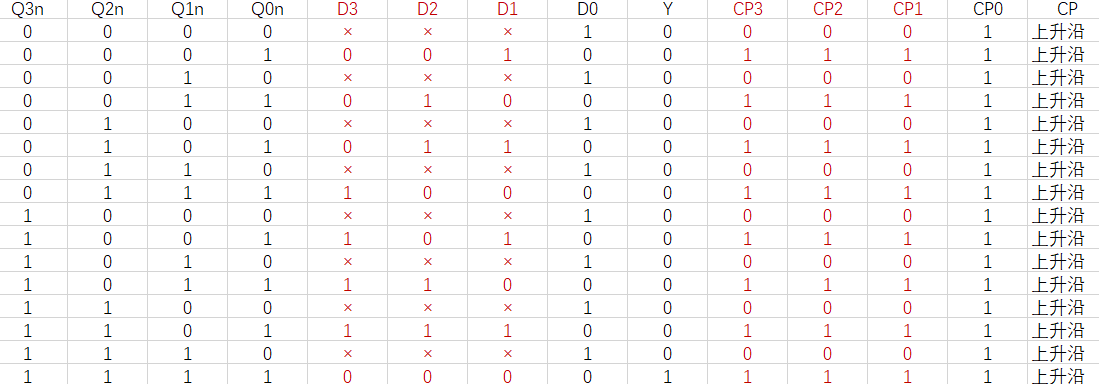
        第五步, 根据绘制的状态激励表求输出方程和状态激励方程:

用卡诺图化简的方式, 求得 D0=Q0n', D1=Q1n', D2=Q2n异或Q1n, D3=Q3n·Q1n'+Q3n·Q2n'+Q3n'·Q2n·Q1n, Y=Q3n·Q2n·Q1n·Q0n.

        第六步, 求次态方程:

        Q3^(n+1)=D3=Q3n·Q1n'+Q3n·Q2n'+Q3n'·Q2n·Q1n, Q0下降沿处有效;

        Q2^(n+1)=D2=Q2n异或Q1n, Q0下降沿处有效;

        Q1^(n+1)=D1=Q1n', Q0下降沿处有效;

        Q0^(n+1)=D0=Q0n', 系统时钟CP上升沿有效.

        (由于电路采用全编码设计方案, 故不需验证电路的自启动功能)

        第七步, 绘制电路逻辑图:

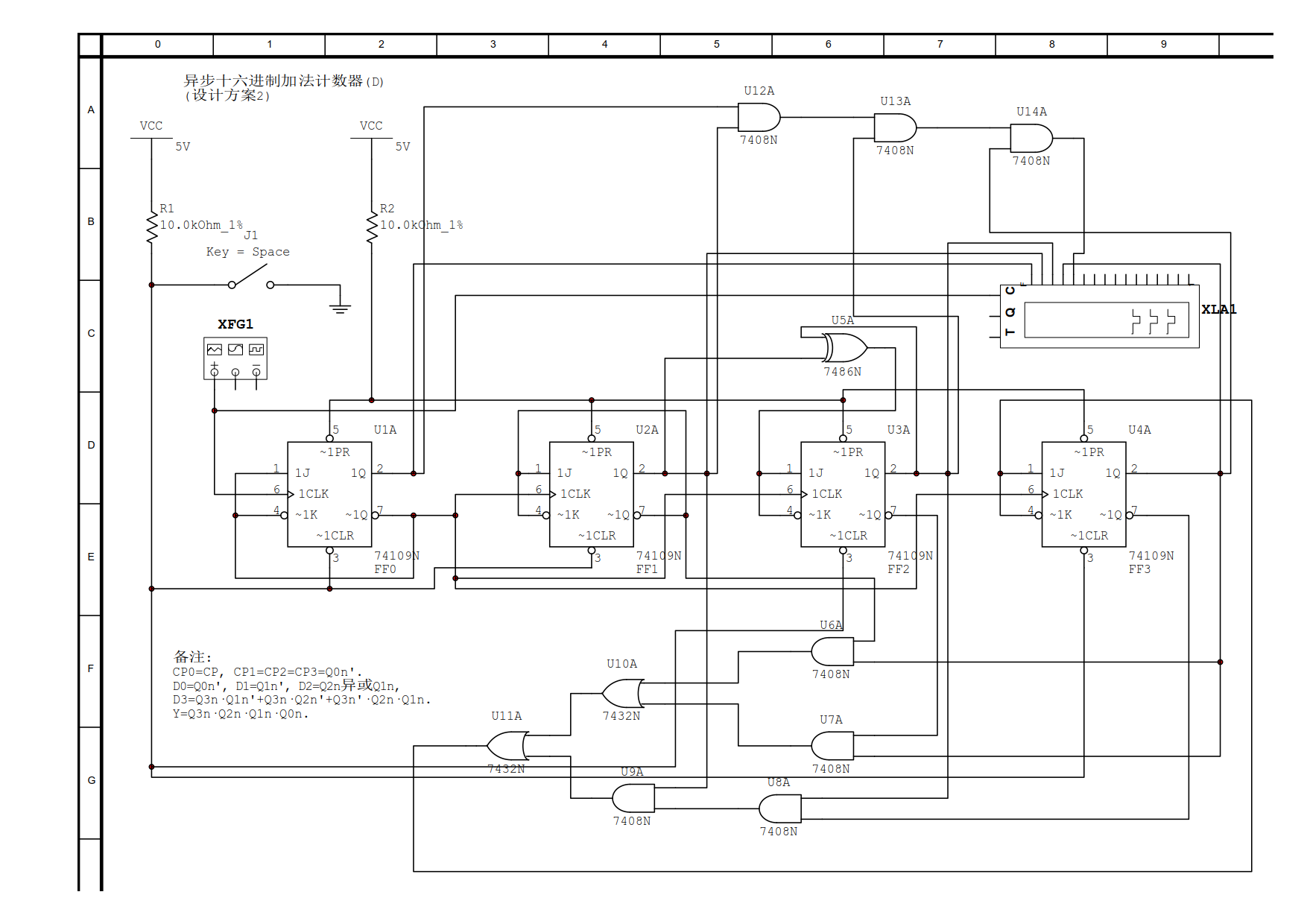
        从上述两种设计方案中可以再次印证"异步时序逻辑电路时钟的选择不唯一"这一观点. 

        大家应对上述设计用例仔细推敲, 以掌握异步时序逻辑电路的设计方法.

最后

以上就是眯眯眼小天鹅为你收集整理的从异步十六进制加法计数器(统一使用上升沿触发的D触发器)的设计, 看异步时序逻辑电路时钟的选择的全部内容，希望文章能够帮你解决从异步十六进制加法计数器(统一使用上升沿触发的D触发器)的设计, 看异步时序逻辑电路时钟的选择所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。