同步四进制可逆加减法计数器分析

183 阅读 0 评论 121 点赞

我是靠谱客的博主幽默蜜蜂，这篇文章主要介绍同步四进制可逆加减法计数器分析，现在分享给大家，希望可以做个参考。

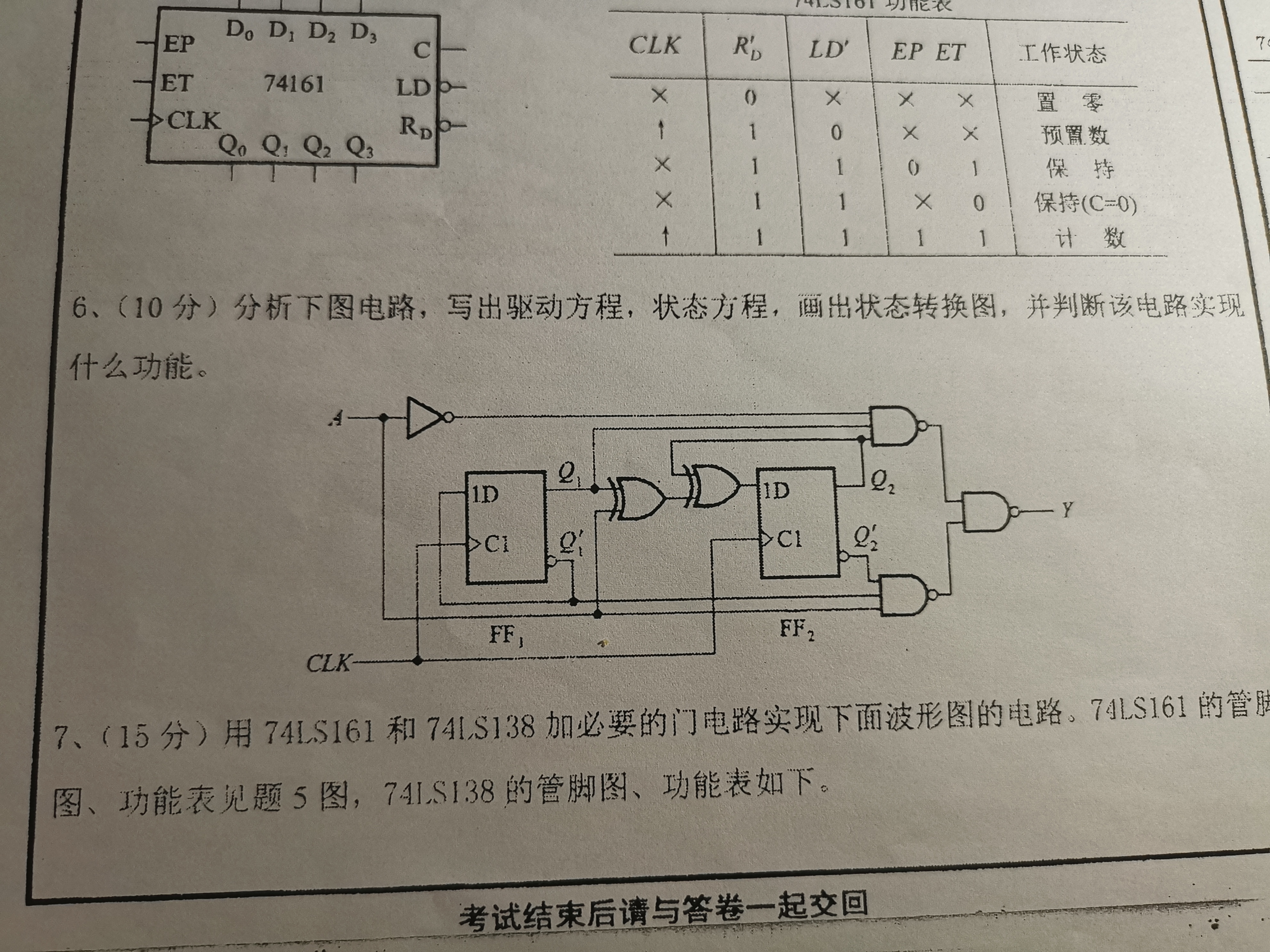
(10分)分析下图电路, 写出驱动方程、状态方程, 并画出状态转换图, 之后判断该电路实现的逻辑功能.

分析同步时序逻辑电路时要遵循的思维过程:

①确定触发器类型(JK触发器/D触发器/......) -> ②写出触发器状态特性方程 -> ③根据逻辑图写出输出方程, 并作可能的化简, -> ④根据逻辑图写出激励方程组, 并作可能的化简, -> ⑤将求出的激励方程组代入触发器状态特性方程, 求出次态方程组, -> ⑥根据求出的次态方程组列状态表, -> ⑦根据绘制好的状态表绘制状态图, -> ⑧仔细观察状态图, 寻找状态转换规律, 最终分析出电路的逻辑功能.

对于Y的推理, 不建议像图片中这样做(我的推理走了弯路) : 应从 $Y=overline{ overline{overline{A}{Q_{1}}^{n}{Q_{2}}^{n}} cdot overline{A cdot overline{{Q_{1}}^{n}} cdot overline{{Q_{2}}^{n}}} }$ 入手.

Y=1时, $overline{overline{A}{Q_{1}}^{n}{Q_{2}}^{n}} cdot overline{A cdot overline{{Q_{1}}^{n}} cdot overline{{Q_{2}}^{n}}}=0$ , 那么 $overline{overline{A}{Q_{1}}^{n}{Q_{2}}^{n}}=0$ 或 $overline{A cdot overline{{Q_{1}}^{n}} cdot overline{{Q_{2}}^{n}}}}=0$ , 则 $overline{A}{Q_{1}}^{n}{Q_{2}}^{n}=1$ 或 $A cdot overline{{Q_{1}}^{n}} cdot overline{{Q_{2}}^{n}}}=1$ .

有了该结论, 我们可以轻松地填充图示卡诺图, 并得出Y的最简与或表达式.