机器学习-吴恩达-笔记-9-聚类

目录

无监督学习：简介

K-均值算法（K-Means）

优化目标

随机初始化

选择聚类数

相似度/距离计算方法

聚类的衡量指标

【此为本人学习吴恩达的机器学习课程的笔记记录，有错误请指出！】

无监督学习：简介

无监督学习就是让计算机学习无标签数据，而不是此前的标签数据。如图：

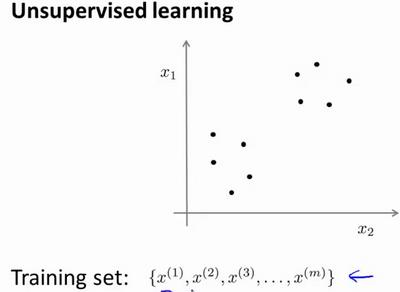
K-均值算法（K-Means）

K-均值是最普及的聚类算法，算法接受一个未标记的数据集，然后将数据聚类成不同的组。

K-均值是一个迭代算法，假设我们想要将数据聚类成 n 个组，其方法为:

步骤一：首先选择????个随机的点，称为聚类中心（ cluster centroids）；

步骤二：对于数据集中的每一个数据，按照距离????个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类。

步骤三：计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置。

重复步骤 2-4 直至中心点不再变化。

迭代 1 次：

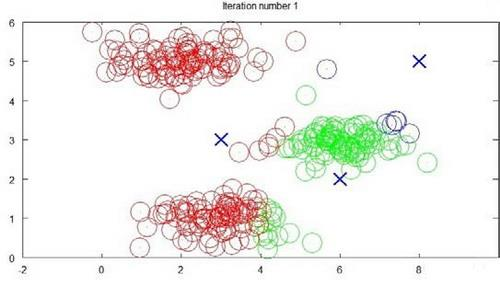
迭代 3 次：

迭代 10 次：

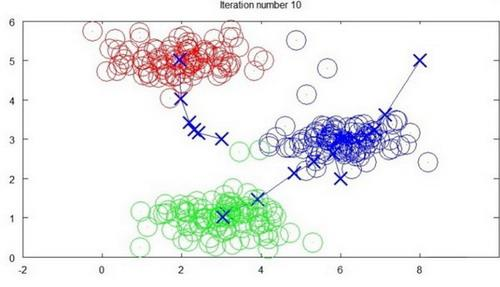
K-均值算法很便利地将数据分为许多不同组，即使在没有非常明显区分的组群的情况下也可以：

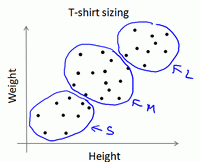
优化目标

K-均值最小化问题，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此 K-均值的代价函数（又称畸变函数 Distortion function）为：

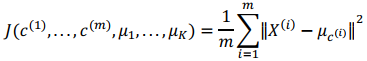
用????1,????2,...,???????? 来表示聚类中心，用????(1),????(2),...,????(????)来存储与第????个实例数据最近的聚类中心的索引。

我们的优化目标便是找出使得代价函数最小的 ????(1),????(2),...,????(????)和????1,????2,...,????????：

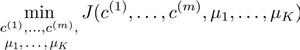
K-均值迭代算法中，第一个循环（分组）是用于减小????(????)引起的代价，而第二个循环（调整中心点）则是用于减小????????引起的代价。迭代的过程一定会是每一次迭代都在减小代价函数，不然便是出现了错误。

随机初始化

在运行 K-均值算法的之前，我们首先要随机初始化所有的聚类中心点：

1. 应该选择???? < ????，即聚类中心点的个数要小于所有训练集实例的数量

2. 随机选择????个训练实例作为聚类中心

K-均值的一个问题在于，它有可能会停留在一个局部最小值处，而这取决于初始化的情况。

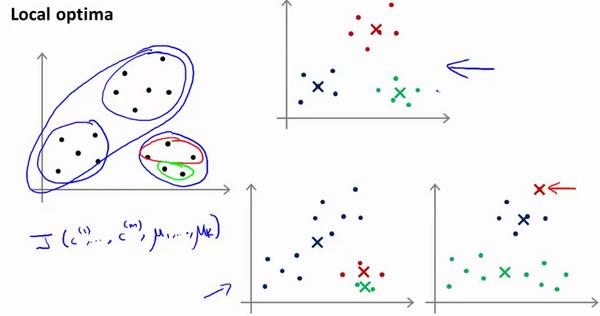
为了解决这个问题，我们通常需要多次运行 K-均值算法，每一次都重新进行随机初始化，最后再比较多次运行 K-均值的结果，选择代价函数最小的结果。这种方法在????较小的时候（ 2--10）还是可行的，但是如果????较大，这么做也可能不会有明显地改善。

选择聚类数

没有所谓最好的选择聚类数的方法，通常是需要根据不同的问题，人工进行选择的。

选择的时候思考运用 K-均值算法聚类的动机是什么，然后选择能最好服务于该目的标聚类数。

选择聚类数目的方法时， 有一个可能会谈及的方法叫作“肘部法则”，也就是K和代价函数的关系：

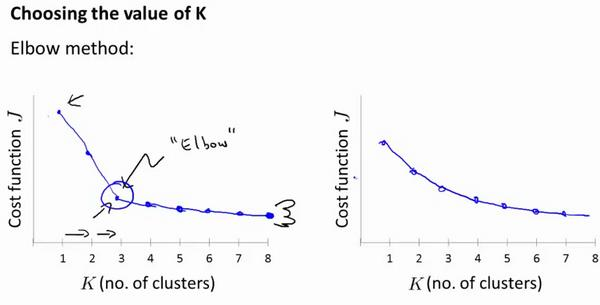
我们可能会得到一条类似于这样的曲线。 像一个人的肘部。应用“肘部法则”的时候， 如果得到了一个像上面类似的图， 那么这将是一种用来选择聚类个数的合理方法。

相似度/距离计算方法

(1). 闵可夫斯基距离 Minkowski/（其中欧式距离： ???? = 2)

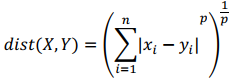
(2). 杰卡德相似系数(Jaccard)，一般用于计算两个集合的相似度：

(3). 余弦相似度(cosine similarity)，一般是计算两个向量的相似度：

????维向量????和????的夹角记做????，根据余弦定理，其余弦值为：

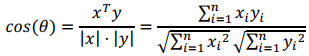
(4). Pearson 皮尔逊相关系数，一般是计算两个向量的相似度：

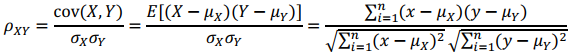
Pearson 相关系数即将????、 ????坐标向量各自平移到原点后的夹角余弦。

聚类的衡量指标

(1). 均一性： ????

类似于精确率，一个簇中只包含一个类别的样本，则满足均一性。其实也可以认为就是正确率(每个聚簇中正确分类的样本数占该聚簇总样本数的比例和)

(2). 完整性： ????

类似于召回率，同类别样本被归类到相同簇中，则满足完整性(每个聚簇中正确分类的样本数占该类型的总样本数比例的和)

(3). V-measure:

均一性和完整性的加权平均：

(4). 轮廓系数

样本 ???? 的轮廓系数： ????(????)

簇内不相似度：计算样本????到同簇其它样本的平均距离为????(????)，应尽可能小。

簇间不相似度：计算样本????到其它簇????????的所有样本的平均距离????????????，应尽可能大。

????(????) 越接近 1 表示样本 ???? 聚类越合理；

????(????) 越接近-1，表示样本 ???? 应该分类到另外的簇中；

????(????) 近似为 0，表示样本 ???? 应该在边界上;

所有样本的????(????)的均值被成为聚类结果的轮廓系数。

(5). ARI

数据集????共有????个元素， 两个聚类结果分别是：

????和????的元素个数为：

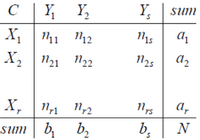
记： ???????????? = |???????? ∩ ????????|

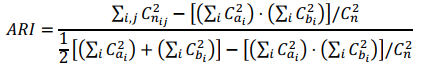
最后

以上就是秀丽小蘑菇为你收集整理的机器学习-吴恩达-笔记-9-聚类的全部内容，希望文章能够帮你解决机器学习-吴恩达-笔记-9-聚类所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。