快速傅里叶变换python_Python的信号傅里叶变换的完美案例，高清图片！,python,求,之,附...

近期做加速度信号的时域与频域分析项目。研究不同频率对信号的影响程度，用到了傅里叶变换以及高通和低通滤波内容。

又把高数详细看了一遍，收获蛮大的。

下面就把成果分享出来。

原信号折线图

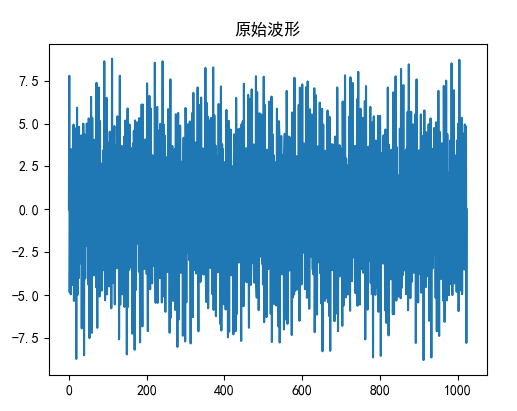
经过傅里叶转换过的双边振幅谱，未求绝对值。

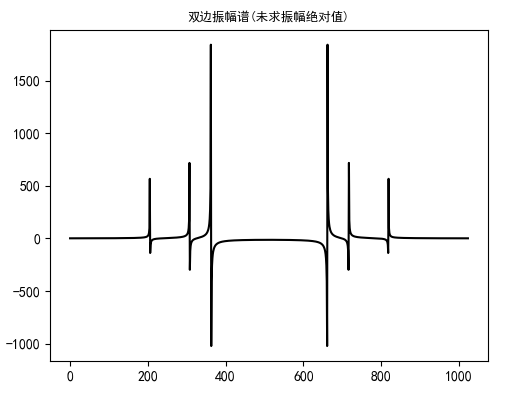
求绝对值后的双边振幅谱。对复数来讲求绝对值就是取实部和虚部模数。

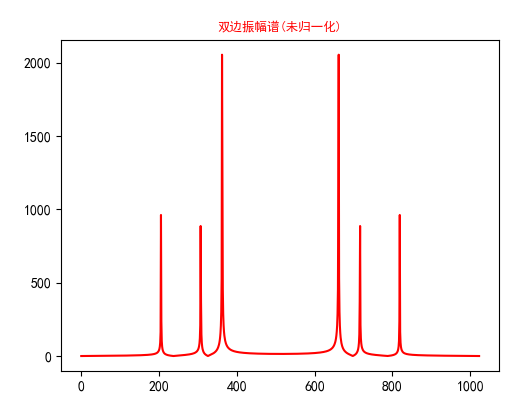
顺便把相位谱也放上来。

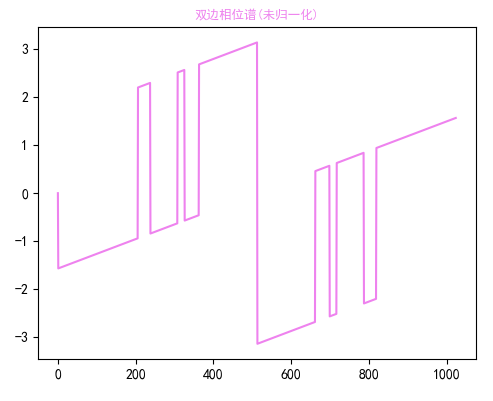
归一化之后的双边振幅谱。

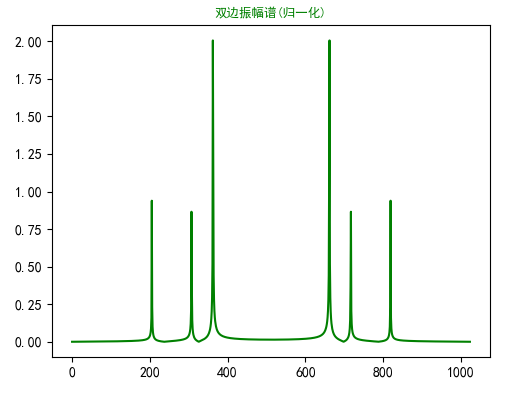
最后把单边振幅谱呈现出来。

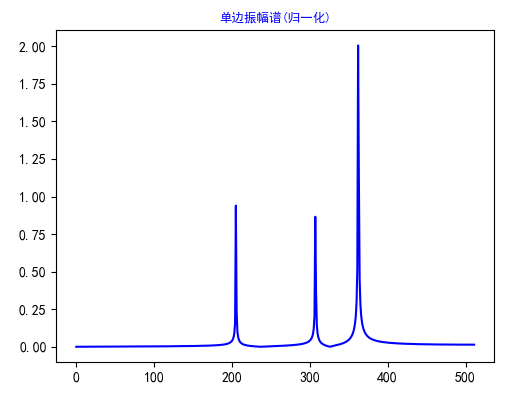
代码如下：

import numpy as np

from scipy.fftpack import fft,ifft

import matplotlib.pyplot as plt

from matplotlib.pylab import mpl

from mpl_toolkits.mplot3d import Axes3D

import time

mpl.rcParams['font.sans-serif'] = ['SimHei'] #显示中文

mpl.rcParams['axes.unicode_minus']=False #显示负号

#采样点选择1400个，因为设置的信号频率分量最高为600赫兹，根据采样定理知采样频率要大于信号频率2倍

a=0

while a<100:

a+=1

x=np.linspace(0,1,1024)

#设置需要采样的信号，频率分量有200，400和600

i=np.random.randint(10,size=3)

fr=np.random.randint(512,size=3)

y=i[0]*np.sin(2*np.pi*fr[0]*x) + i[1]*np.sin(2*np.pi*fr[1]*x) +i[2]*np.sin(2*np.pi*fr[2]*x)

fft_y=fft(y) #快速傅里叶变换

N=x.size

x = np.arange(N) # 频率个数

half_x = x[range(int(N/2))] #取一半区间

time.sleep(1)

abs_y=np.abs(fft_y) # 取复数的绝对值，即复数的模(双边频谱)

angle_y=np.angle(fft_y) #取复数的角度

normalization_y=abs_y/N #归一化处理（双边频谱）

normalization_half_y = normalization_y[range(int(N/2))] #由于对称性，只取一半区间（单边频谱）

plt.clf() #清除刷新前的图表，防止数据量过大消耗内存

plt.subplot(231)

plt.plot(x,y)

plt.title('原始波形')

plt.subplot(232)

plt.plot(x,fft_y,'black')

plt.title('双边振幅谱(未求振幅绝对值)',fontsize=9,color='black')

plt.subplot(233)

plt.plot(x,abs_y,'r')

plt.title('双边振幅谱(未归一化)',fontsize=9,color='red')

plt.subplot(234)

plt.plot(x,angle_y,'violet')

plt.title('双边相位谱(未归一化)',fontsize=9,color='violet')

plt.subplot(235)

plt.plot(x,normalization_y,'g')

plt.title('双边振幅谱(归一化)',fontsize=9,color='green')

plt.subplot(236)

plt.plot(half_x,normalization_half_y,'blue')

plt.title('单边振幅谱(归一化)',fontsize=9,color='blue')

plt.pause(0.4) #设置暂停时间，太快图表无法正常显示

plt.ioff() # 关闭画图的窗口，即关闭交互模式

plt.show()

后面我还继续进行了高通和低通滤波功能，由于从传感器获得的是加速度信号，我还需要进行二次积分获得位移数据。

最后

以上就是笨笨野狼为你收集整理的快速傅里叶变换python_Python的信号傅里叶变换的完美案例，高清图片！,python,求,之,附...的全部内容，希望文章能够帮你解决快速傅里叶变换python_Python的信号傅里叶变换的完美案例，高清图片！,python,求,之,附...所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。