好久没有更新量化分析相关的内容，本节将介绍如何通过傅里叶变换求解一组数据当中可能存在的周期性，后续将应用本节的结果实际在量化程序中进行应用。本文计算方法不一定正确，欢迎大家多多指正，并在评论区进行交流。

1 离散傅里叶变换

        离散傅里叶变换的公式如下：

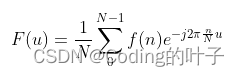
        其中N为原始数据的长度，f(n)为原始数据，即随时间变化的序列。F(u)为傅里叶变换结果，可以看到F(u+1)和F(u)的每个频率分量相差1/N个频率间隔。因此，f(n)经过傅里叶变换后得到的F(u)在频域 上的频率间隔为1/N。

        另外，当u=0时，e指数部分取值为1。因此，F(0)是f(n)的平均值。

2 求解数组周期

        利用傅里叶变换求解数组周期的步骤：

        （1）利用1中的公式，求解傅里叶变换结果F(u)。

        （2）求解（1）中傅里叶变换的幅值。

        （3）求解（2）中傅里叶幅值的峰值，幅值越大的地方表示周期性越明显。

        （4）假设峰值出现在u=k处，那么根据1中分析，对应的频率为k/N，那么相应的周期为N/k。

3 示例程序

import numpy as np
from scipy.signal import find_peaks
import matplotlib.pyplot as plt


x = np.array([ 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1])
N = x.shape[0]
print(N)
f = np.fft.fftn(x)  #全部变换，f[0]为全部取值累加结果
f = f[:N//2]

peaks, p = find_peaks(abs(f), height=0.1)
print(peaks)

# print(f)
# plt.plot(abs(x), '.')
plt.plot(abs(f), '.')
print(abs(f))
print(f[6])
real =  f[13].real
im = f[13].imag
theta = np.arctan(im/(real+1e-6))
pos = np.angle(f[13])/2/np.pi*5
print(np.angle(f[13]))
print(theta, pos)
# plt.show()

4 求解结果

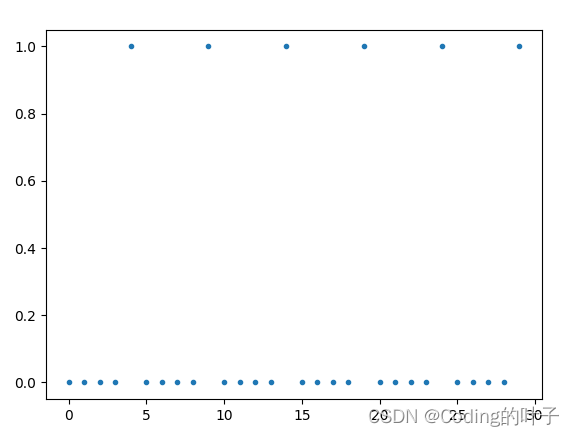
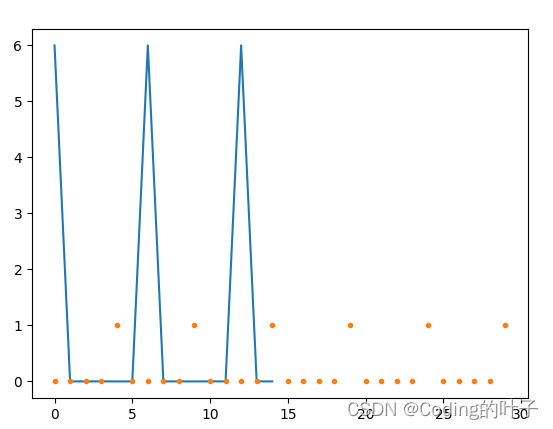
         T =5。

        求解后的周期，最好进行验证，以免出现误差。本文计算方法不一定正确，欢迎大家多多指正，并在评论区进行交流。

更多三维、二维感知算法和金融量化分析算法请关注“乐乐感知学堂”微信公众号，并将持续进行更新。

最后

以上就是高兴溪流为你收集整理的【量化投资】离散傅里叶变换求数组周期1 离散傅里叶变换2 求解数组周期3 示例程序4 求解结果的全部内容，希望文章能够帮你解决【量化投资】离散傅里叶变换求数组周期1 离散傅里叶变换2 求解数组周期3 示例程序4 求解结果所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。