MATLAB中应用pwelch（）函数实现功率谱估计——官方说明中文文档

62 阅读 0 评论 41 点赞

我是靠谱客的博主含糊大地，最近开发中收集的这篇文章主要介绍MATLAB中应用pwelch（）函数实现功率谱估计——官方说明中文文档，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

最近又从头开始学有关信号处理中，功率谱估计的内容，在MATLAB中可以使用pwelch（）函数实现Welch平均周期法对信号的谱估计结果，pwelch函数中存在较多参数，对概念理解不深的初学者感觉很难看懂官方说明文档和，网上感觉也没有特别好的说明文章，但都说的不是非常清楚，先对MATLAB官网上pwelch（）函数的说明文档进行翻译，原文链接

基本函数参数

pxx = pwelch(x)

pxx = pwelch(x,window)

pxx = pwelch(x,window,noverlap)

pxx = pwelch(x,window,noverlap,nfft)

[pxx,w] = pwelch(___)

[pxx,f] = pwelch(___,fs)

[pxx,w] = pwelch(x,window,noverlap,w)

[pxx,f] = pwelch(x,window,noverlap,f,fs)

[___] = pwelch(x,window,___,freqrange)

[___] = pwelch(x,window,___,spectrumtype)

[___] = pwelch(x,window,___,trace)

[___,pxxc] = pwelch(___,'ConfidenceLevel',probability)

pwelch(___)

描述：

pwelch（）函数利用Welch'平均功率图法返回信号x的功率谱密度（PSD）pxx。当x是向量时，它被当做一个单通道信号，当x是矩阵是，x的每一列被当做一个通道的信号，其psd结果相对应与psd的每一列。如果x是实值信号，则pxx是单边谱估计，如果x是复数信号，则pxx是双边谱估计。在默认设置中，x被分成8段，重叠率为50%的片段。每个片段上添加一个hamming窗。pwelch利用这种修正后的周期图法来对psd进行估计。当然你不能将x刚好分为满足50%重叠的8个片段，为了实现功能，函数会对x的长队进行相应地自动裁剪。

pwelch（）函数是使用方法如上，现在对每个参数的具体意义进行详细说明：

X：进行功率谱估计的有限长输入序列；
WINDOW：指定窗函数，默认值为hamming窗；
NFFT：DFT的点数， NFFT> X，默认值为256；
Fs ：绘制功率谱曲线的抽样频率，默认值为1；
Pxx：功率谱估计值；
F：Pxx值所对应的频率点
NOVERLAP指定分段重叠的样本数，如果NOVERLAP=L/2，则可得到重叠50%的Welch法平均周期图
如果使用boxcar窗，且NOVERLAP=0，则可得到Bartlett法的平均周期图

[pxx,w] = pwelch(___)返回的是标准化后的频率向量w，如果pxx是单边谱估计，那么w的范围就是0到pi，如果pxx是双边谱估计，那么w的范围就是0到2pi。

[pxx,f] = pwelch(___,fs) 返回一个频率向量f。fs时每个单位时间的样本s，那么f的单位是Hz，那么f的范围是0到fs/2，对于复值信号来说，f的范围是0到fs。且fs必须是pwelch的第五个输入变量，如果为了输入fs，而其他参数使用默认值的话，其他参数可以设置为空[].

下面具体举一个例子，一序列含有白噪声和两个频率间隔很近的余弦信号，信号的表达式为：

N=512; Nfft=1024; Fs=1; n=0:N-1;
xn=cos(0.3*pi*n)+cos(0.32*pi*n)+randn(size(n));
M=input('M=')
window=boxcar(M); noverlap=M/2;
[Pxx2 w]=pwelch(xn,window,noverlap,Nfft);
figure; plot(w,10*log10(Pxx2)),grid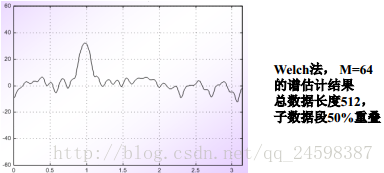

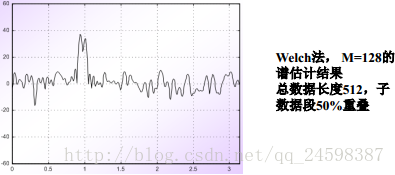
对比周期图法和Welch发，周期图谱估计曲线的波动很大，即估计的方差较大，而Welch法谱估计曲线较为平滑，方差减小，但分辨率降低；对Welch法，当数据分段数增加，各段数据长度较短时，谱的分辨率明显下降，而谱估计曲线较为平滑，方差较小；反之，当数据分段数减小，各段数据长度较长时，谱分辨率明显提高，而谱估计曲线波动较大，方差较大