【C语言编程】切比雪夫多项式

问题：

已知：切比雪夫多项式：

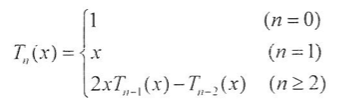
编写一程序，输入n,x，并输出0～n的所有T_n(x)的值。

解析：

本题用递归函数求解，没什么难度，代码如下：

#include <stdio.h>
int T(int n,int x){
    int k;
    if(n==0)
        k=1;
    else if(n==1)
        k=x;
    else 
        k=2*x*T(n-1,x)-T(n-2,x);
    return k;
}
int main() {
    int n,x;
    printf("Input n,x(n>=0):");
    scanf("%d,%d",&n,&x);
    if(n<0) {
        printf("error!");
        return 0;
    }
    printf("%d",T(n,x));
    return 0;
}

扩展

• 概述
  切比雪夫多项式是以 俄国著名数学家切比雪夫(Tschebyscheff，又译契贝雪夫等，1821一1894)的名字命名的重要的特殊函数，第一类切比雪夫多项式Tn和第二类切比雪夫多项式Un(简称切比雪夫多项式)。源起于多倍角的余弦函数和正弦函数的展开式，是与棣美弗定理有关、以递归方式定义的多项式序列，是计算数学中的一类特殊函数，对于注入连续函数逼近问题，阻抗变换问题等等的数学、物理学、技术科学中的近似计算有着非常重要的作用
• 源来
  切比雪夫多项式在逼近理论中有重要的应用。这是因为第一类切比雪夫多项式的根（被称为切比雪夫节点）可以用于多项式插值。相应的插值多项式能最大限度地降低龙格现象，并且提供多项式在连续函数的最佳一致逼近。
• 基本性质
  对每个非负整数n， T_n(x) 和 U_n(x) 都为 n次多项式。 并且当n为偶（奇）数时，它们是关于x 的偶（奇）函数， 在写成关于x的多项式时只有偶（奇）次项 [1] 。
  n 1时，Tn的最高次项系数为 ，n=0时系数为1。

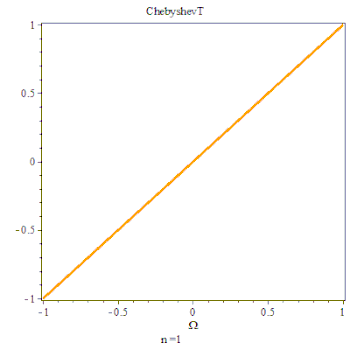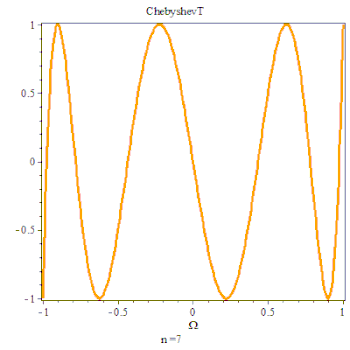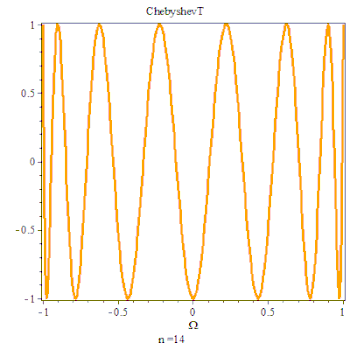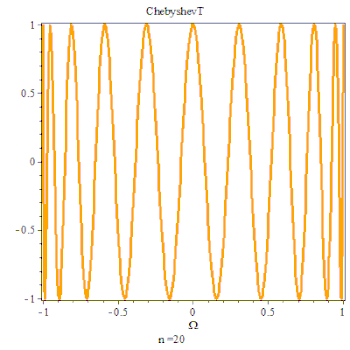
最后

以上就是兴奋蜻蜓为你收集整理的【C语言编程】切比雪夫多项式的全部内容，希望文章能够帮你解决【C语言编程】切比雪夫多项式所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。