系列文章目录

• Delay Line 简介及其 C/C++ 实现
• LFO 低频振荡器简介及其 C/C++ 实现
• 【音效处理】Delay/Echo 算法简介
• 【音效处理】Vibrato 算法简介
• 【音效处理】Reverb 混响算法简介
• 【音效处理】Compressor 压缩器算法简介

1. 卷积

在讨论快速卷积之前，让我们先聊聊「卷积」。卷积的数学定义非常简单，两个离散信号 $x[n]$ 与 $h[n]$ 的卷积为：
$$x[n]\ast h[n]=\sum _{k=-\infty }^{\infty }x[k]h[n-k]=y[n],n\in \mathbb{Z}$$
如何直观的理解这个公式呢？说实话，我看了很多资料，例如：

• 如何通俗易懂地解释卷积？
• “卷积”其实没那么难以理解

在看这些资料的时候，似乎看懂了，但过了几天回头面对着卷积公式我又说不上来它在干什么了。不过没关系，今天的话题只需要对卷积有个笼统的感觉就可以了。

卷积在信号处理中非常重要，在 【音频处理】如何“认识”一个滤波器？ 中我们提到：

信号$x(n)$经过 LTI 滤波器后得到 $y(n)$，这个过程可以表示为冲激响应$h(n)$与$x(n)$的卷积：
$$y(n)=(h\ast x)(n)$$

通俗的来说，假设现在我们有一个信号系统，它是一个黑盒，我们不知道它的功能是什么，只知道输入一个信号，它会吐出另一个信号。现在你有个任务，手上有 1000 条输入信号，你想要得到这个黑盒给出的输出信号，这时候你会怎么做？

方法一，我就辛苦一点，1000 条数据慢慢输入，然后得到输出，非常耗时。
方法二，敏锐地察觉到输入信号 x(n) 经过黑盒处理的过程，其实就是卷积的过程，那么只要我们能够获得黑盒系统的冲击响应 h(n)，那么剩下的工作就是在电脑上将 x(n) 和 h(n) 卷积下就可以了。

很明显，方法二是高效且机智的，无论再多的输入信号，黑盒的冲击响应 h(n) 是不变的，我们要抓住这个不变量。

那么，系统的 h(n) 如何获取呢？很简单，只需要对这个系统输入一个理想的单位冲激信号 $\delta (t)$ 就可以了。当然，在现实世界中，不存在理想的 $\delta (t)$ ，通常可以用短促且高能的信号来替代，例如雷声，枪声，打板声等等。

在音频处理领域中，混响效果也可以通过卷积来实现。例如，我们可以在「浴室」空间下，播放短促且高能的声音，并录制空间的回音音频，这就得到了该空间的 h(n)。接下来，如果你想要「浴室」的混响效果，那么只需要将你的输入音频与 h(n) 做卷积操作即可。

2. 快速卷积

卷积很重要，应用范围很广泛，但它有一个很致命的缺陷：计算复杂度太高了。我们以上面提到的混响实现为例，录制得到的 h(n) 长度为 N，输入信号有 M，那么通过卷积算法得到混响效果需要：

1. 输出的每个采样需要乘法 N 次
2. 输出的每个采样需要加法 N 次
3. 输出长度为 N，所以有乘法 N * M 次，所有有加法 N * M 次，算法复杂度是 O(N*M)

如果音频的采样率为 44100，那么 1s 的 h(n)，去处理 1min 的输入音频，那么共需要 44100 * 60 * 44100 乘法和 44100 * 60 * 44100 加法。这计算量即使高端 PC 电脑也要跑上好久。以我个人的 mac m1 为例，一个 h(n) 为 4s，x(n) 为 25s 的输入，使用 numpy 的 convolve 进行卷积，需要大概 20s 时间。

卷积算法实在是太慢了，为此人们发明了快速卷积（Fast Convolution）算法来提升卷积的速度。接下来将介绍各种快速卷积算法，主要参考下面两篇文章，建议有余力的同学可以去看原文：

• Fast Convolution: FFT-based, Overlap-Add, Overlap-Save, Partitioned
• Partitioned convolution algorithms for real-time auralization

下面所有代码你都可以在 github - fast_convolution 中找到，其中 python 目录包含了 python 实现，C++ 实现则是在 src 目录下，在 example 目录下有不同卷积实现的使用示例。

2.1 FFT 卷积

稍微学习过信号处理的同学，应该都知道「时域上做卷积，就是在频域上做乘积」，利用这个定理，我们将 h(n) 和 x(n) 通过快速傅里叶变换（FFT）得到频域信号 $H(\omega )$ 和 $X(\omega )$，然后相乘得到 $Y(\omega )$，最后将 $Y(\omega )$ 通过 IFFT 从频域变换为时域即可。流程图如下：

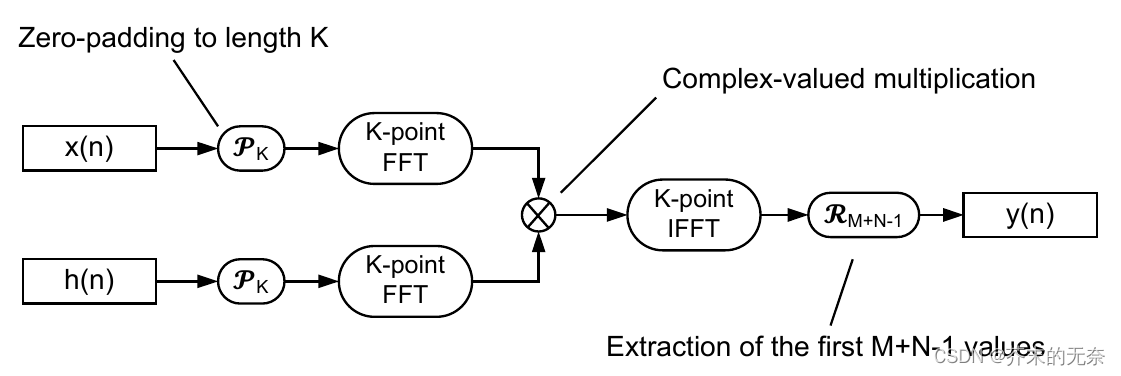
在上述流程中，有几个问题需要进行思考：

1. h(n) 与 x(n) 长度通常是不相同的，但在频域相乘的操作中，我们需要 $H(\omega )$ 和 $X(\omega )$ 是大小相同的。因此需要通过 zero-padding 的形式，将 h(n) 和 x(n) 填充到长度为 K。
2. 那么 K 是多大呢？这篇文章的 2.5.2 小节告诉我们它必须满足 $K\ge M+N-1$
3. 那么输出的 y(n) 长度是多少呢？在我们的实现中长度是 M+N-1，但也有不同的实现，参考 numpy-convolution 中的 mode 参数。

经过上述几个问题的思考后，我们的 fft 卷积算法呼之欲出，python 代码如下：

def pad_zeros_to(x, new_length):
    output = np.zeros((new_length,))
    output[:x.shape[0]] = x
    return output

def next_power_of_2(n):
    return 1 << (int(np.log2(n - 1)) + 1)

def fft_convolution(x, h, K=None):
    Nx = x.shape[0]
    Nh = h.shape[0]
    Ny = Nx + Nh - 1
    
    if K is None:
        K = next_power_of_2(Ny)
        
    X = np.fft.fft(pad_zeros_to(x, K))
    H = np.fft.fft(pad_zeros_to(h, K))
    
    Y = X*H
    
    y = np.real(np.fft.ifft(Y))
    
    return y[:Ny]

代码很简单：

1. 首先计算 K 的大小，满足 K >= M + N -1 的条件。FFT 通常对 2 的次方长度支持较好，因此我们还取了一个 next_power_of_2 来确保 K 是 2 的次方
2. 调用 pad_zeros_to 将 x 和 h 都填充到 K 大小，接着调用 fft 来计算频域结果，然后频域做乘法 Y = X*H
3. 最后用 ifft 从频域转回时域得到最终的卷积结果

2.2 分块卷积

虽然 FFT 卷积已经很快了，但它需要输入 x(n) 全部数据，这样就有两个问题：

1. x(n) 如果很长，那么 FFT 计算将会耗费非常多的内存资源，对于移动端或者算力比较弱的机器非常不友好
2. 在实际的音频、音乐场景中，我们要求实时性，也就是说我们无法得到全部 x(n)。例如直播场景中，音频流可以认为是无限长的。

为此，人们又提出了分块卷积，例如当囤积了 256/64/32 个数据时，就进行一次卷积，这样满足了实时性的要求，且可以将算法延迟控制在较低的水平。

2.2.1 Overlap-Add 分块卷积

首先介绍 overlap-add 分块卷积算法，用基于FFT的卷积法将每个传入的块与完整的滤波器进行卷积，存储适当的许多过去的卷积结果，并在与我们处理的输入信号相同长度的块中输出其后续部分的和。处理的流程图如和代码下：

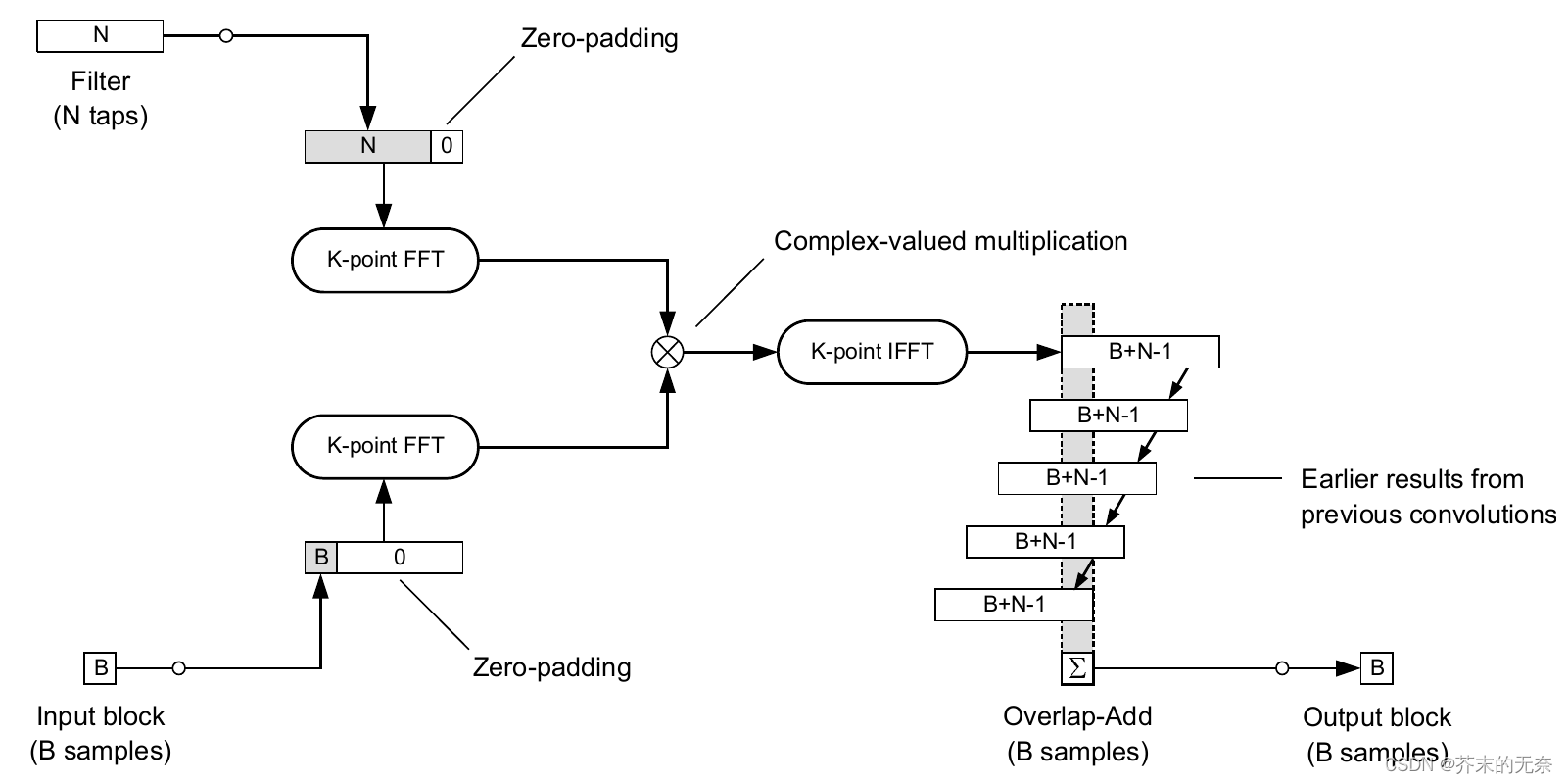
def overlap_add_convlution(x, h, B, K=None):
    M = len(x)
    N = len(h)
    
    num_input_blocks = np.ceil(M/B).astype(int)
        
    output_size = M + N - 1
    y = np.zeros((output_size,))
    
    for n in range(num_input_blocks):
        xb = x[n*B:(n+1)*B]
        
        u = fft_convolution(xb, h, K)
        
        y[n*B:n*B + len(u)] += u
    
    return y

在上述实现中，为了方便起见，我并没有实现实时版本的算法，但你要确信它是可以做到的。Overlap add 块卷积最后得到结果的时候，进行了 overlap add，非常像 STFT 中的 overlap 操作。

2.2.2 Overlap-Save 块卷积

Overlap-Add方案的一个重要缺点是必须存储和汇总计算出的部分卷积。我们有办法可以优化吗？

另一种方法叫做 Overlap-Save。它是基于存储适当数量的输入块而不是输出块，后者比计算出的卷积短。输入数据块以先入先出的方式存储在一个长度为 K 的 buffer 中，也就是说，每个新的输入样本块都会转移缓冲区中所有先前存储的样本，丢弃最古老的 B 个样本。然后，我们用零填充的滤波器系数进行基于 K 点的 FFT 卷积。处理的流程图如和代码下：

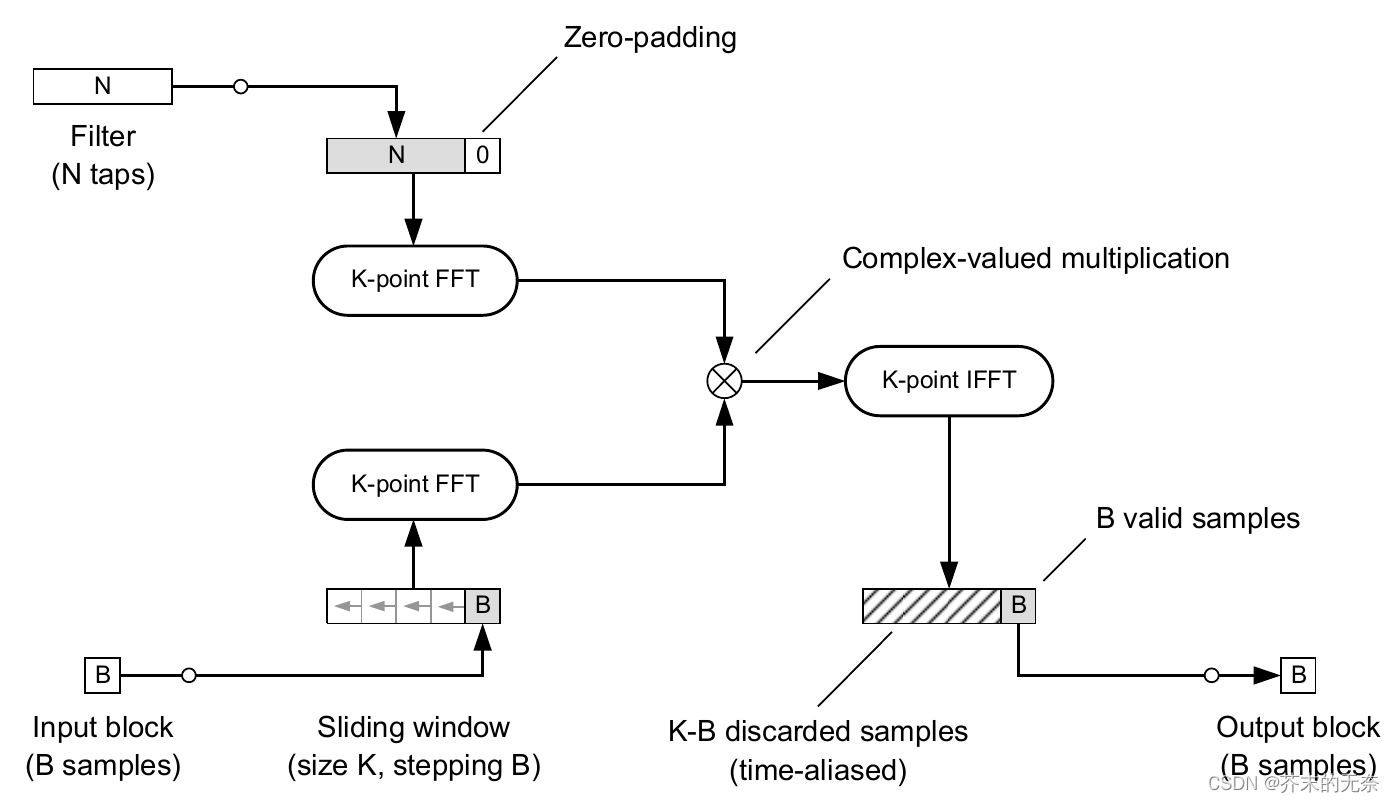
def overlap_save_convolution(x, h, B, K=None):
    M = len(x)
    N = len(h)

    if K is None:
        K = next_power_of_2(B + N - 1)
        
    # Calculate the number of input blocks
    num_input_blocks = np.ceil(M / B).astype(int) 
                     + np.ceil(K / B).astype(int) - 1

    # Pad x to an integer multiple of B
    xp = pad_zeros_to(x, num_input_blocks*B)

    output_size = num_input_blocks * B + N - 1
    y = np.zeros((output_size,))
    
    # Input buffer
    xw = np.zeros((K,))

    # Convolve all blocks
    for n in range(num_input_blocks):
        # Extract the n-th input block
        xb = xp[n*B:n*B+B]

        # Sliding window of the input
        xw = np.roll(xw, -B)
        xw[-B:] = xb

        # Fast convolution
        u = fft_convolution(xw, h, K)

        # Save the valid output samples
        y[n*B:n*B+B] = u[-B:]

    return y[:M+N-1]

Overlap-Save 的方案在实时场景下更容易实现，且比 Overlap-Add 性能更好。但其中的 sliding window 部分实现起来比较复杂。

3. 均匀分割卷积算法

如果我们要与输入进行卷积的滤波器也有相当长的长度（例如，当它代表一个有相当长混响时间的大殿的脉冲响应时），我们可能要同时对x(n)和 h(n) 都进行分区。这里要介绍的是「均匀分割卷积算法」。它的处理的流程图如和代码下：

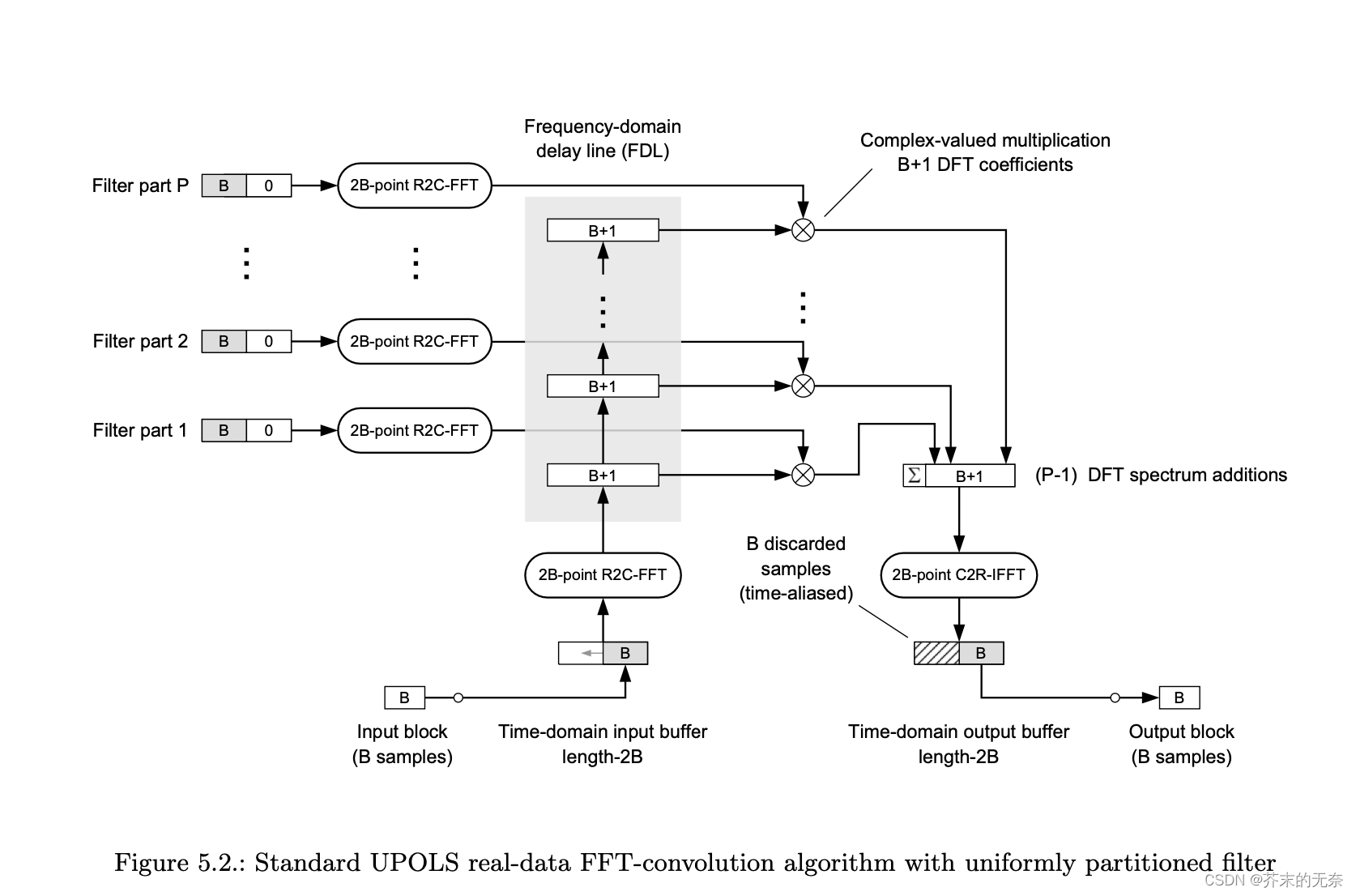
def realtime_uniformly_partitioned_convolution(x, h, B):
    M = len(x)
    N = len(h)
    P = np.ceil(N/B).astype('int')
    num_input_block = M//B
    
    print('num_input_block:',num_input_block)
    
    output = np.zeros(M)
    
    # precalculate sub filters fft
    sub_filters_fft = np.zeros((P, 2*B), dtype=np.complex64)
    for i in range(P):
        sub_filter = h[i*B:i*B + B]
        sub_filter_pad = pad_zeros_to(sub_filter, 2*B)
        sub_filters_fft[i,:] = np.fft.fft(sub_filter_pad)
        
    
    # input blocks
    freq_delay_line = np.zeros_like(sub_filters_fft)
    xw = np.zeros(2*B)
    for i in range(num_input_block):
        block_x = x[i*B:i*B + B]
        xw = np.roll(xw, -B)
        xw[-B:] = block_x
        
        xw_fft = np.fft.fft(xw)
        
        # inser fft into delay line
        freq_delay_line = np.roll(freq_delay_line, 1, axis=0)
        freq_delay_line[0,:] = xw_fft
        print(freq_delay_line)

        # ifft
        s = (freq_delay_line*sub_filters_fft).sum(axis=0)
        # print(s)
        ifft = np.fft.ifft(s).real[-B:]
        # print(o)
        output[i*B:i*B + B] = ifft
        
    return output

以上，所有的代码都可以在 github - fast_convolution 中找到。此外还有 C++ 版本的实现，在 example 目录下有均匀分割卷积的实时播放场景的示例，你只需要修改 input_file 和 impulse_file 的路径即可。关于 impuse_file 你可以在 vtolani95/convolution 找到一些。

3.1 混响实现

下面的视频是利用均匀分割卷积做混响的效果：

具体的实现中，为了控制输出音频的音量大小，还引入了一个 scale 的变量。这个变量可以作为一个算法参数让用户进行调节。

4 总结

这篇文章中我们介绍了卷积在信号系统中的重要意义，卷积算法复杂度为 O(N^2)，为了加速卷积计算，人们提出了快速卷积算法，本文介绍了 FFT 卷积，Overlap-Add 和 Overlap-Save 块卷积，以及均匀分割卷积算法。算法的相关实现都在 github - ast_convolution，包括 python 版本和 C++ 版本。

5 参考

• 如何通俗易懂地解释卷积？
• “卷积”其实没那么难以理解
• 【音频处理】如何“认识”一个滤波器？
• 「珂学原理」- 冲激响应
• Fast Convolution: FFT-based, Overlap-Add, Overlap-Save, Partitioned
• Partitioned convolution algorithms for real-time auralization
• 时域卷积定理和频域卷积定理 - 知乎
• github - fast_convolution

最后

以上就是真实秀发为你收集整理的【音频处理】Fast Convolution 快速卷积算法简介系列文章目录1. 卷积2. 快速卷积3. 均匀分割卷积算法4 总结5 参考的全部内容，希望文章能够帮你解决【音频处理】Fast Convolution 快速卷积算法简介系列文章目录1. 卷积2. 快速卷积3. 均匀分割卷积算法4 总结5 参考所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。