文章的内容整理自网络,仅Matlab代码部分进行了部分修正,具体而言:
理论部分来自:现代通信原理2.5:确定信号的能量谱密度、功率谱密度与自相关函数
估计和代码部分来自: 随机信号功率谱密度估计
PS1 推荐使用周期图法进行功率密度谱估计。
PS2 系统学习一下胡广书老师的书!
目录
A、信号的能量谱密度、功率谱密度与自相关函数的理论
B、功率密度谱估计方法介绍
C、Matlab 代码及结果展示
A、信号的能量谱密度、功率谱密度与自相关函数的理论
内容转自现代通信原理2.5:确定信号的能量谱密度、功率谱密度与自相关函数

B、功率密度谱估计方法介绍
下面内容转自 随机信号功率谱密度估计
一、实验目的
1.深入理解随机信号功率谱密度估计
2.掌握在Matlab平台上进行信号功率谱密度估计的基本方法
二、实验原理
1. 随机信号功率谱密度定义
定义随机信号信号的功率谱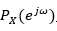 为
为
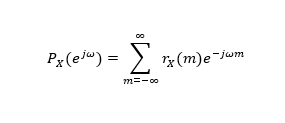
其中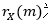 为随机信号的自相关函数。
为随机信号的自相关函数。
功率谱反映了信号的功率在频域随频率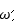 分布,因此
分布,因此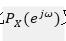 又称为功率谱密度。[1]
又称为功率谱密度。[1]
2. 经典谱估计(非参数谱估计)方法简介
经典谱估计的方法主要包括两种方法:周期图法和自相关法。
周期图法[1](直接法)
周期图法又称为直接法,它是把随机信号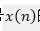 的N点观察数据
的N点观察数据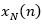 视为一个能量有限信号,直接取
视为一个能量有限信号,直接取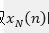 的傅里叶变换,得
的傅里叶变换,得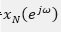 ,然后再取其幅值的平方,并除于N,作为对
,然后再取其幅值的平方,并除于N,作为对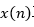 真实功率谱
真实功率谱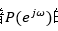 的估计。以
的估计。以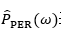 表示用周期图法估计的功率谱,则
表示用周期图法估计的功率谱,则
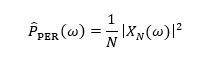
自相关法[1](间接法)
此方法的理论基础是维纳-辛钦定理。1958年Blackman和Tukey 给出了这一种方法的具体实现,即由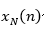 估计出自相关函数
估计出自相关函数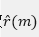 ,然后对
,然后对 的功率谱,记之为
的功率谱,记之为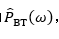 ,并以此作为对
,并以此作为对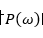 的估计,即
的估计,即
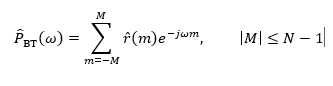
因为这种方法求出的功率谱是通过自相关函数间接得到的,所以称为间接法,又称自相关法或BT法。当M较小时,上式计算量不是很大,因此,该方法是在FFT问世之前(即周期图法被广泛应用之前)常用的谱估计方法。
3. 参数模型谱估计方法简介[1]
参数模型法是现代谱估计的主要内容,参数模型法的思路如下。

三、实验步骤
1. 构造模拟信号
构造模拟信号
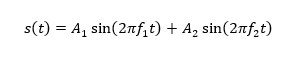

2. 使用经典谱估计方法对信号进行谱估计
1) 周期图法
Matlab中Prierdogram()函数就是运用周期图法进行谱估计。调用格式如下:
[psdestx,Fxx] = periodogram(xn,rectwin(length(xn)),length(xn),Fs);
其中输入参数xn为待估计的离散信号,rectwin(length(xn))表示窗长为xn点的矩形窗(rectangle window),Fs表示采样频率。
输出参数Fxx表示频率,psdestx为对应Fxx频率的功率谱密度。
为了使周期图法得到的功率谱密度更为平滑,提出了许多改进的方法,Welch平均周期图法就是其中一种,在matlab中pwelch()函数就是使用该方法进行功率谱估计,pwelch()函数的调用格式如下:
pwelch(xn,hamming(256),128,1024,Fs)
输入参数xn为输入信号,hamming(256)为窗长为256的汉明窗,Fs为信号采样频率。调用后可绘制得到信号功率谱密度图,如需要观察得到的功率谱密度数值,可以添加相应的输出参数,相应可以参阅matlab帮助文档。
2) 相关函数法
相关函数法是先求信号是自相关函数,再根据维纳辛欣定理,功率谱密度就是自相关函数的傅里叶变换,对自相关函数求傅里叶变换,得到功率谱密度。
需要用到matlab中xcorr()函数,其调用格式如下:
cx=xcorr(xn,'biased');
其中输入参数xn为待求自相关函数的信号,'biased'表示使用有偏差的自相关函数求法。
输出参数cx即为信号xn的自相关函数。
3. 使用现代谱估计方法对信号进行谱估计
伯格(Brug)谱估计是一种AR谱估计方法,可调用matalb中pburg函数,其调用格式如下:
pburg(xn,5,1024,Fs)
输入参数xn为信号,Fs为采样频率。调用后可绘制得到信号功率谱密度图,如需要观察得到的功率谱密度数值,可以添加相应的输出参数,相应可以参阅matlab帮助文档。
四、实验结果与分析
1. 经典谱估计方法和现代谱估计方法比较
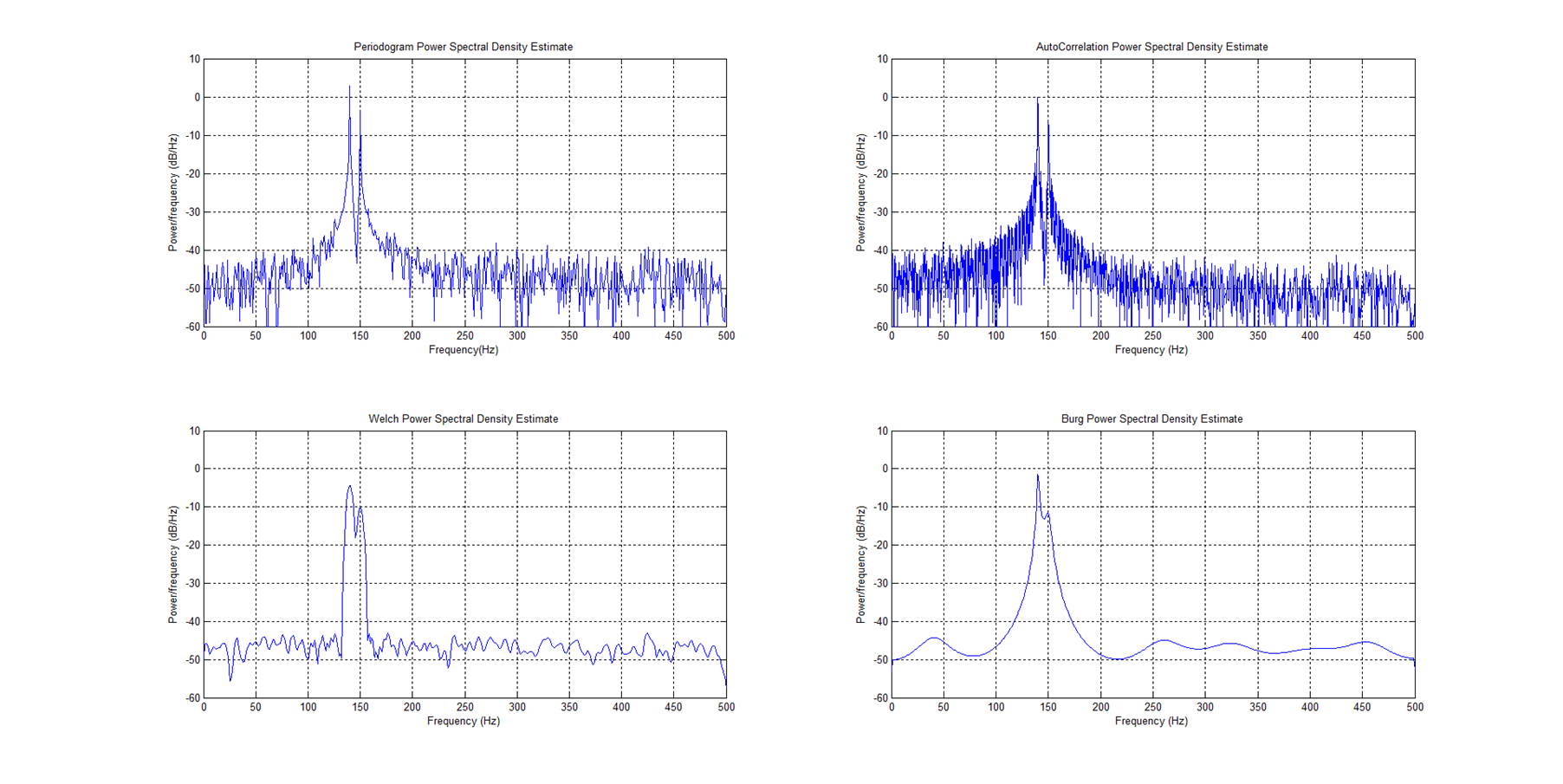
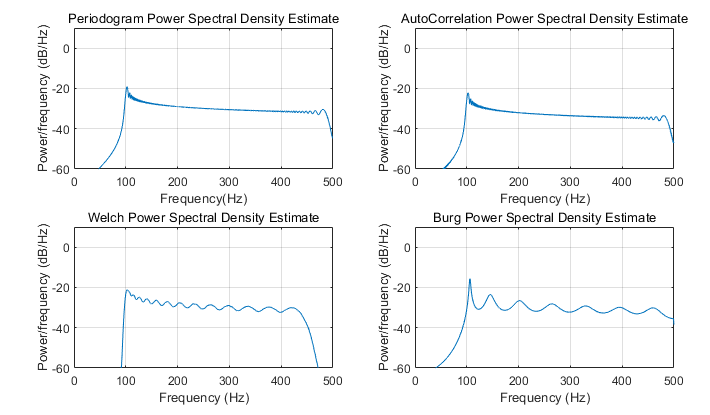
图4.1 不同功率谱估计方法比较
如图4.1所示,对比周期图法(periodogram)和平均周期图法(Welch),验证了Welch法得到的图要比周期图法得到的功率谱密度图光滑。自相关法和周期图法得到的功率谱估计在140Hz和150Hz处锋比较尖锐,频率分辨率要比Welch平均周期图法高。现代AR谱估计Brug方法同样可以在140Hz和150Hz处得到尖锐的谱峰,同时其估计的功率谱密度图也很平滑。
2. AR谱估计中模型阶数对谱估计结果的影响
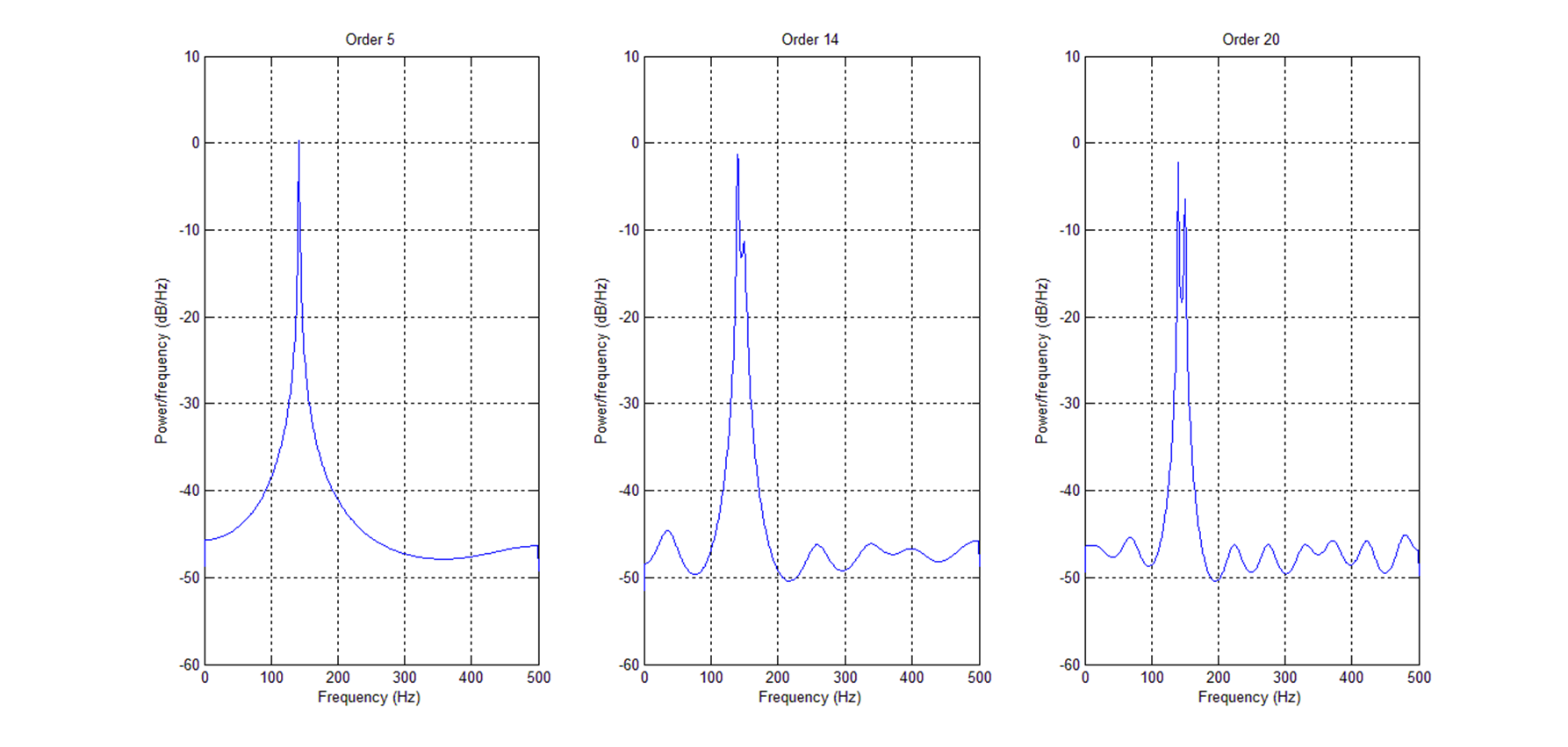 (a) (b) (c)
(a) (b) (c)
图4.2 AR模型阶数对谱估计的影响
(a)5阶 (b)14阶 (c)20阶
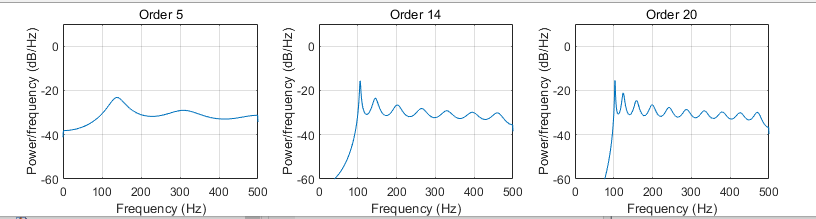
如图4.2,对比不同AR模型阶数对功率谱估计的影响,发现阶数较低时,在140Hz-150Hz频率范围左右,只出现一个谱峰,没有得到实际的两个谱峰,频率分辨率不够,随着模型阶数的增加,到阶数达到14时,可以有效地区分140Hz和150Hz处的两个谱峰,有较好的频率分辨率,随着模型阶数的继续增加,在真峰(140Hz和150Hz)附近的假峰会随着增多。
五、实验结论
通过对比经典和现代不同谱估计方法,可以发现,现代谱估计方法既有较好的频率分辨率,又是能使功率谱密度较为平滑,可以很到的得到信号谱峰。
现代AR谱估计中,模型的阶数选择是一个很重要的问题,选择合适的阶数,可以有效的检查出有效信号的谱峰,如果模型阶数过低,则频率分辨率不够,可能会丢失有效信号谱峰,如果模型阶数过高,则可能出现假峰。
六、参考文献
[1] 胡广书. 数字信号处理:理论、算法与实现(第三 版)[M]. 北京:清华大学出版社,2012.
C、Matlab 代码及结果展示
%% 构造模拟信号
clc
clear
close all
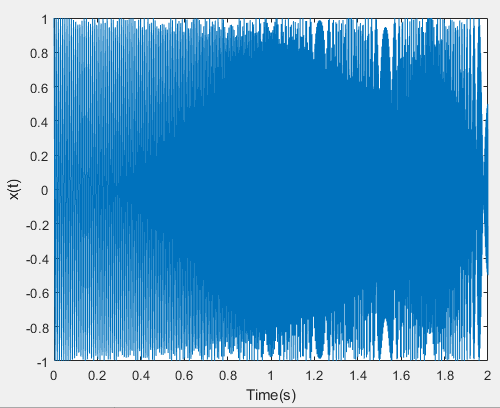
t = 0:0.001:2;
xn = chirp(t,100,1,200,'quadratic');
Fs = 1/0.001;
figure(1)
plot(t,xn);
xlabel('Time(s)')
ylabel('x(t)')
%% 周期图法
figure(2);
subplot(2,2,1)
[psdestx,Fxx] = periodogram(xn,rectwin(length(xn)),length(xn),Fs);
plot(Fxx,10*log10(psdestx)); % 其中10*log10(),是dB和功率之间的转换关系!
grid on;
xlabel('Frequency(Hz)'); ylabel('Power/frequency (dB/Hz)');
title('Periodogram Power Spectral Density Estimate');
axis([0 500 -60 10])
%% 自相关函数法(BT法)
subplot(2,2,2)
cx=xcorr(xn,'biased'); %计算自相关函数
cxdft = fft(cx);
psdx = abs(cxdft)/Fs;
freq = 0:Fs/length(psdx):Fs/2;
plot(freq,10*log10(psdx(1:length(freq)))); grid on;
title('AutoCorrelation Power Spectral Density Estimate');
xlabel('Frequency (Hz)'); ylabel('Power/frequency (dB/Hz)');
axis([0 500 -60 10])
%% Welch 平均周期法
subplot(2,2,3)
pwelch(xn,hamming(256),128,1024,Fs);
axis([0 500 -60 10])
%% Burg法 AR参数谱估计
figure(2)
subplot(2,2,4)
pburg(xn,14,1024,Fs)
axis([0 500 -60 10])
set(gcf,'color',[1 1 1]);
%% 讨论不同的AR阶数对Brug法的影响
figure(3)
subplot(1,3,1)
pburg(xn,5,1024,Fs)
axis([0 500 -60 10])
title('Order 5')
subplot(1,3,2)
pburg(xn,14,1024,Fs)
axis([0 500 -60 10])
title('Order 14')
subplot(1,3,3)
pburg(xn,20,1024,Fs)
axis([0 500 -60 10])
title('Order 20')
set(gcf,'color',[1 1 1]);程序结果
信号图:
各类方法结果对比:
不同的AR阶数对Brug法的影响
最后
以上就是迷路大碗最近收集整理的关于随机信号功率谱密度函数理论、估计方法及MATLAB代码的全部内容,更多相关随机信号功率谱密度函数理论、估计方法及MATLAB代码内容请搜索靠谱客的其他文章。








发表评论 取消回复