信号频谱的几种表示方式及其关系

这里将连续信号和离散信号的频谱的几个式子总结在一起。方便使用时查阅。

一个时域连续信号x(t)，假设其能量有限，并且频域带宽有限，则可以对其进行傅立叶变换求其频谱。

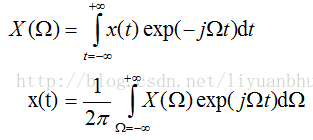
上面的式子中，X(Ω)称为信号的频谱。如果我们在频域用f来作为自变量。则上面的式子改写为：

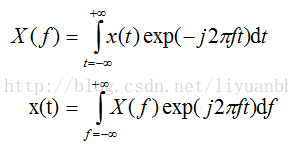
这两种频谱表示间的关系很简单。

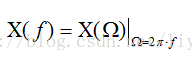
相应的，有所谓的能量等式：

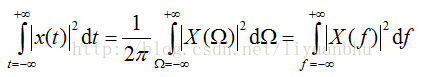
对连续信号进行采样，就得到了离散信号。设采集频率为 fs，采样时间间隔为Δ。那么离散信号x[n] 与连续信号 x(t) 的关系如下：

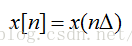
离散信号的频谱通常写为：

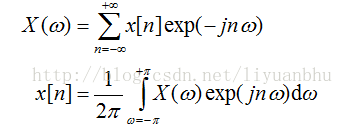
这里的ω与连续信号的Ω之间的关系如下：

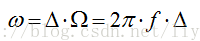
如果用f作为频域自变量，则：

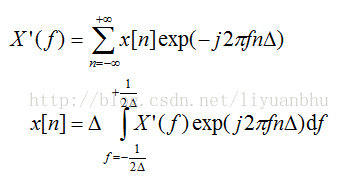
这里用了X’(f) 是为了与连续信号频谱表示相区别。X’(f) 与连续信号频谱X(f) 有什么关系呢？简单的推导可知当信号采样频率满足乃奎斯特采样定律时，X’(f) 与连续信号频谱X(f) 有简单的联系。

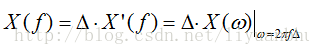
有些教科书上（比如程乾生教授所著的数字信号处理教材），会给出这样的离散信号频谱的定义：

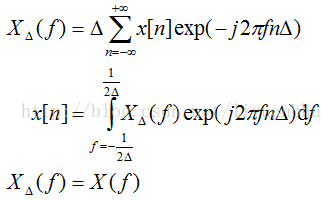
对应的能量等式如下：

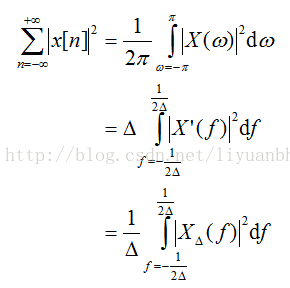
从上面能量等式，还可以得到如下关系：

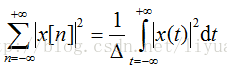
这其实就是积分近似计算中常用的矩形算法。相应的，信号通过一个线性系统（用h(t)表示）后的输出y(t)与x(t) 的关系如下；

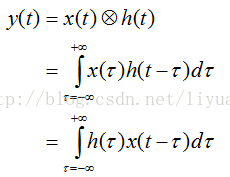
如果我们对x(t)、h(t) 和y(t)都进行采样，得到x[n]、h[n]和y[n]，并且采样过程满足采样定律的要求。那么我们利用 x[n]和h[n] 就应该可以计算出 y[n]。

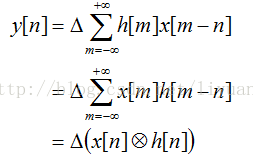
实际应用中，我们不可能采集无限长时间的数据，因此我们用于处理的离散信号通常都限定在一定长度。这时它的频谱为：

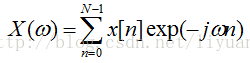
对于N个数据点的序列，我们实际上只需要计算N个频点的值。

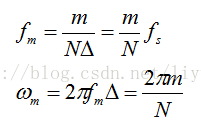
因此，可以得到有限离散频谱公式如下：

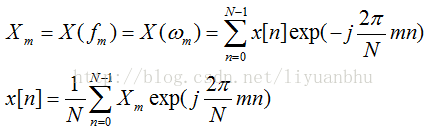
最后

以上就是忧心蓝天为你收集整理的信号频谱的几种表示方式及其关系的全部内容，希望文章能够帮你解决信号频谱的几种表示方式及其关系所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。