【数学建模】【matlab】二维矩形排样代码实现题目来源及衍生背景二维矩形排样的实现

84 阅读 0 评论 56 点赞

我是靠谱客的博主落寞纸鹤，最近开发中收集的这篇文章主要介绍【数学建模】【matlab】二维矩形排样代码实现题目来源及衍生背景二维矩形排样的实现，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目来源及衍生背景

题目来源于2021年mathorcup数学建模比赛D题第一题，最初时间紧迫，采用randchoose()函数随机选取一款订单，有点类似于蚁群算法，只是缺少了“信息素”这个概念，没有一种回溯的效率提升。但是其由于原题中数量过于庞大，第一题采用蚁群算法计算以及调试时间过长，在比赛期间心情紧张可能导致得不偿失，因此最终选择将其简化。

并且在长里为了控制宽度一致，每行上放的都是同一种订单。

如果希望对订单要求比较高，是不规则的排样，并且不能保证每行放置的都是同一种订单，那可以采用“最低水平面”方法，可以关注我，我写的“最低水平面算法”文章。

我在代码中加入了详细的注释，所以原理部分写的不是很详细，大家可以抓住“先排长，再排宽”这句话直接看代码部分。

二维矩形排样的实现

算法原理

简单理解成先长里排到排不下，再对宽进行排件，并且注意每行放置的都是同一种订单，如下图所示：

这个图有点问题，应该吧LSj2和WSj1的位置互换
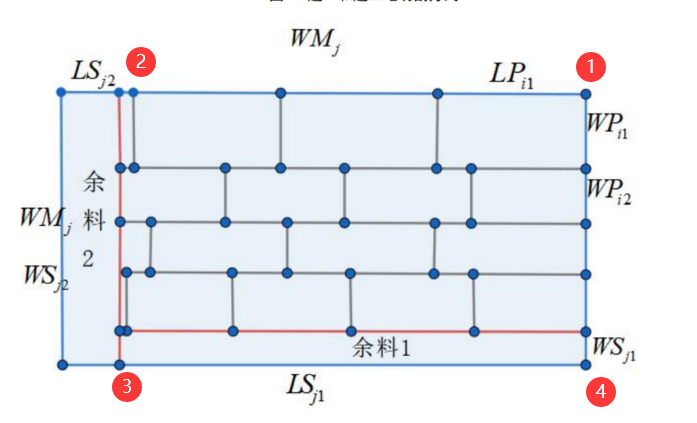
在这里插入图片描述
首先对1 --> 2这个过程进行遍历，在十种原料的条件下，遍历五种订单中放的下该件的情况，放置后再对宽进行排布。

最后计算余料的时候，可以完整的得到左边和下边的两块余料。

重点难点

首先，这个图有点问题，应该吧LSj2和WSj1的位置互换

其中有两个难以快速理解的点，大家可以先记着，看到的时候再回来看。

ws2:在上图中为余料2在长的方向上边的长度

ls1:在上图中为余料在宽的方向上边的长度

其次，47行开始为原题中限制余料规格的要求，大家可以根据自己题目的要求进行更改

算法源码

function mathorcup_1()
%% 数据的导入与预定义
product = xlsread('附件3_4.xlsx', '订单', 'B2 : G16'); % 长度、宽度、需求量、浮动比例、种类
material = xlsread('附件3_4.xlsx', '原料', 'B2 : E11'); % 长度、宽度、库存
PLAN = cell(10, 6); % 存放计划切割方案的元组
plan = zeros(10, 10); %
%% 二维矩形的排样
for j = 1 : 10 % 对十种原料进行遍历
    % 对长进行循环
    if(material(j, 1) > min(product(1 : 5, 1))) % 如果原料的长>卷料订单中长的最小值
        
        i_list = find(product(1 : 5, 1) < material(j, 1)); % 保存满足放置条件的订单的位置
        wsl = material(j, 2); % 原料剩余可用的宽度
        lsl = material(j, 1); % 原料剩余可用的长度
        num_kind_width = zeros(1, 5); % 5种订单宽的切割方案
        num_kind_length = zeros(1, 5); % 5种订单长的切割方案
        % 对宽进行循环
        while(wsl > min(product(1 : 5, 2))) % 当原料剩余可用的宽度 > 卷料订单中宽的最小值
            
            i = randchoose(i_list, 1); % 随机从满足放置条件的订单中选一个
            if(wsl - product(i, 2) < 0) % 如果在放置后，卷料剩余可用的宽度仍大于零则继续
                continue
            end
            % 当某一个节点之后卷料剩余可用宽度小于零执行以下内容
            wsl = wsl - product(i, 2); % 更新原料剩余可用宽度
            num_kind_width(i) = num_kind_width(i) + 1; % 更新原料剩余可用长度
            num_kind_length(i) = fix(material(j, 1) / product(i, 1)); % 计算长上放置的订单数量
            % num_kind_width_length存放格式：1~5:五种订单宽的数量，6~10：五种订单长的数量
            num_kind_width_length = [num_kind_width, num_kind_length]; % 每种原料中长、宽放置的订单数量
        end
        % 将第j种原料的五种订单的各个数量存放进plan数组
        % plan存放格式:第j行:第几种原料，每一行后面的10个数:第几种原料放置各个订单的长和宽的数量
        for k = 1 : 10
            plan(j, k) = num_kind_width_length(k);
        end
        
        ws2 = material(j, 1) - max(plan(j, 6 : 10) .* product(1 : 5, 1)'); % max()求得原料切割订单后与余料的一个切面
        ls2 = material(j, 2); % 原料的宽度
        ls1 = ls1 - ws2;
        
        % 长度余量
        S_Product = 0;
        for n = 1 : 5
            S_Product = S_Product + plan(j, n) * plan(j, n + 5) * product(n, 6);
        end
        
        % 以下为原题中判断余料是否满足标准的条件设置，可以根据题意进行更改
        S_surplus = 0;
        if(wsl > 100 && lsl > 50000)
            S_surplus = S_surplus + wsl * lsl;
        end
        if(ws2 > 2000 && ls2 > 1000)
            S_surplus = Surplus + ws2 * ls2;
        end
        R = (S_surplus + S_Product) / material(j, 4);
        % 数据的输出
        PLAN{j, 6} = R;
        for n = 1 : 5
            PLAN{j, n} = [num_kind_width_length(n), num_kind_width_length(n + 5)];
        end
    end
end
end