

前言回顾
#第三话#介绍了MATLAB内部的绘图命令。比如如何利用函数命令控制数据图的坐标轴、线型、颜色等;如何绘制子图与动图;如何在标题或者坐标轴标签中增加LaTeX公式。
此外,小编说一哈下写本系列推送的目的不是为了让大家对MATLAB的用法有全面的了解或者替代书本,因为本人也做不到。出发点是为大家整理最常用的命令和最容易犯的错误,可以指导大家更高效地自学。更多的自学资料在上方专辑内有。 本文中用到的所有代码和额外资料在 阅读原文 中也有。
请输入标题 abcdefg
本期概述
“
优化算法
首先了解一下什么是函数句柄——优化传参基础;
主体部分介绍MATLAB内两个代表性优化函数的用法:
1、fmincon: 全称是Find minimum of constrained nonlinear multivariable function,即求约束非线性多变量函数的最小值。当然,这个里面包含了求解线性问题、无约束问题等。因此该算法几乎是和问题无关的。
2、particleswarm: 粒子群优化求解函数,用法上与fmincon有很多重叠之处,将较为快速地讲解。这里不涉及粒子群算法的具体流程,有兴趣的可以点击阅读原文自行补充。
——最后会举例比较说明
函数句柄??
在进入本期优化函数之前,必须先理解什么是函数句柄。函数句柄(function handle)是MATLAB中的一类特殊的数据结构,它的地位类似于其它计算机语言里的函数对象(Javascript,Python),函数指针(C++),或者函数引用(Perl)。作用是将一个函数封装成一个变量,使其能够像其它变量一样在程序的不同部分传递。MATLAB中的函数句柄在调用时和普通函数没有任何区别。
函数句柄主要有两种语法:
【A】handle = @functionname
——给已有函数functionname(x)起一个别名,之后应用handle(x)与functionname(x)是完全一样的;
【B】handle = @(x) cos(x)
——创建一个没有名字的函数,用handle引用。
相当于建立了一个函数文件:
function y=anonymous(x)
y=cos(x);
end
这里介绍的比较简单,更详细的内容可以点击阅读原文或者百度。如果完全可以理解,那下面的内容就没有问题;如果不是特别能接受,那可能看起来会有些阻力。
fmincon
[x,fval]=fmincon(fun,x0,A,b,...%换行
Aeq,beq,lb,ub,nonlcon)

上述MATLBA表达式给出的是fmincon的基础用法,更多的参数说明可以参考doc fmincon,但是对于初学者来讲这些已经完全够用了;上述公式给出的是一般的非线性约束优化问题的模型。
下面一一对应进行解释
1、f(x)是目标函数,对应于fun。这里的fun需要是函数句柄而不能是函数表达式:
fmincon(@fun,x0,A,.........)%这里的@fun代表已经写好的函数文件的句柄
function f = fun(x)
f = ...% 具体的函数可以写在内部
end
当然也可以是匿名函数
fun = @(x)sin(x(1))*cos(x(2)) %这是一个函数句柄
但不可以是
syms x
fun=cos(x) %这是符号表达式,不接受!
这里都是求函数的最小值,如果是最大值问题,在目标函数前面加一个负号简单转换即可。
2、x是设计变量集合,也就是所有变量所组成的向量。
比如x=[a b c d];
那么就是x(1)=a;x(2)=b,如此类推,以对应于实际问题。
x0对应初值点,根据已有条件做出设置,无特殊要求,保证在可行域内即可。当然,会影响收敛速度和解的精度。
3、A*x<=b 是线性不等式约束,将所有的约束写成不等式组的形式,即可得到对应的系数矩阵A和右端项b。
4、Aeq*x=beq 是线性等式约束,也就是一个方程组,Aeq,beq的定义与第三点相仿。显然等式约束是可以向不等式约束进行转化的。比如Ax=b,可以拆分成A*x<=b &A*x>=b这两个约束,所以大家其实可以灵活运用。
5、c(x)<=与ceq(x)=0分别是非线性不等式约束和非线性等式约束。由于是非线性的,所以无法用数值矩阵表示,所以通常写成函数来传递,nonlcon就是同时对应了这两个约束,下面看一个例子:
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [];
end%
以上定义了一个函数unitdisk,它返回的是x经过非线性运算得到的值[c,ceq],因为此处unitdisk是函数,和第1点一样,所以传入其函数句柄进行优化。
nonlcon = @unitdisk;
x0 = [0,0];
x= fmincon(fun,...,nonlcon,...);
这个非线性约束的构造稍微抽象一点也更加灵活,需要仔细想一下,但是如果大家的问题都是线性约束,那么就无需考虑这一项。
6、lb和ub分别是变量的下界和上界。
fmincon例子
例子采用的目标函数是非线性函数,约束是二个线性不等式约束和一个非线性不等式约束,二维问题。
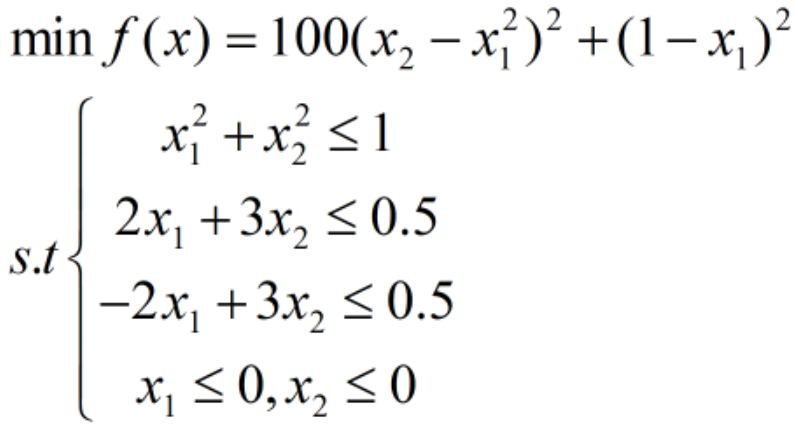
先将目标函数写出来,可以单独保存成一个.m函数文件:
function f = rosenbrock1(x)
f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;
end
再将非线性约束写出来,这里需要注意修改成
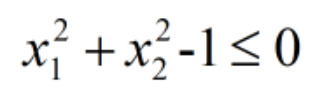
因为在标准模型中对应非线性约束的右端项全部都是0。其次需要将该约束写成函数,也可以保存成一个单独的函数文件。
function [c,ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];
接着处理两个线性约束,写成矩阵形式
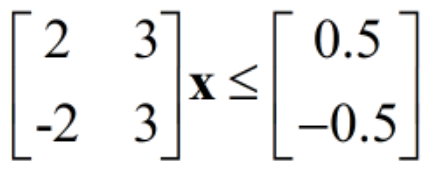
即A=[2 3;-2 3];b=[0.5 -0.5];注意这里的b必须是列向量。最后还有两个很简单的上下界约束,lb=[ ],ub=[0 0]。lb=[ ]的原因是此处没有约束x的下界。
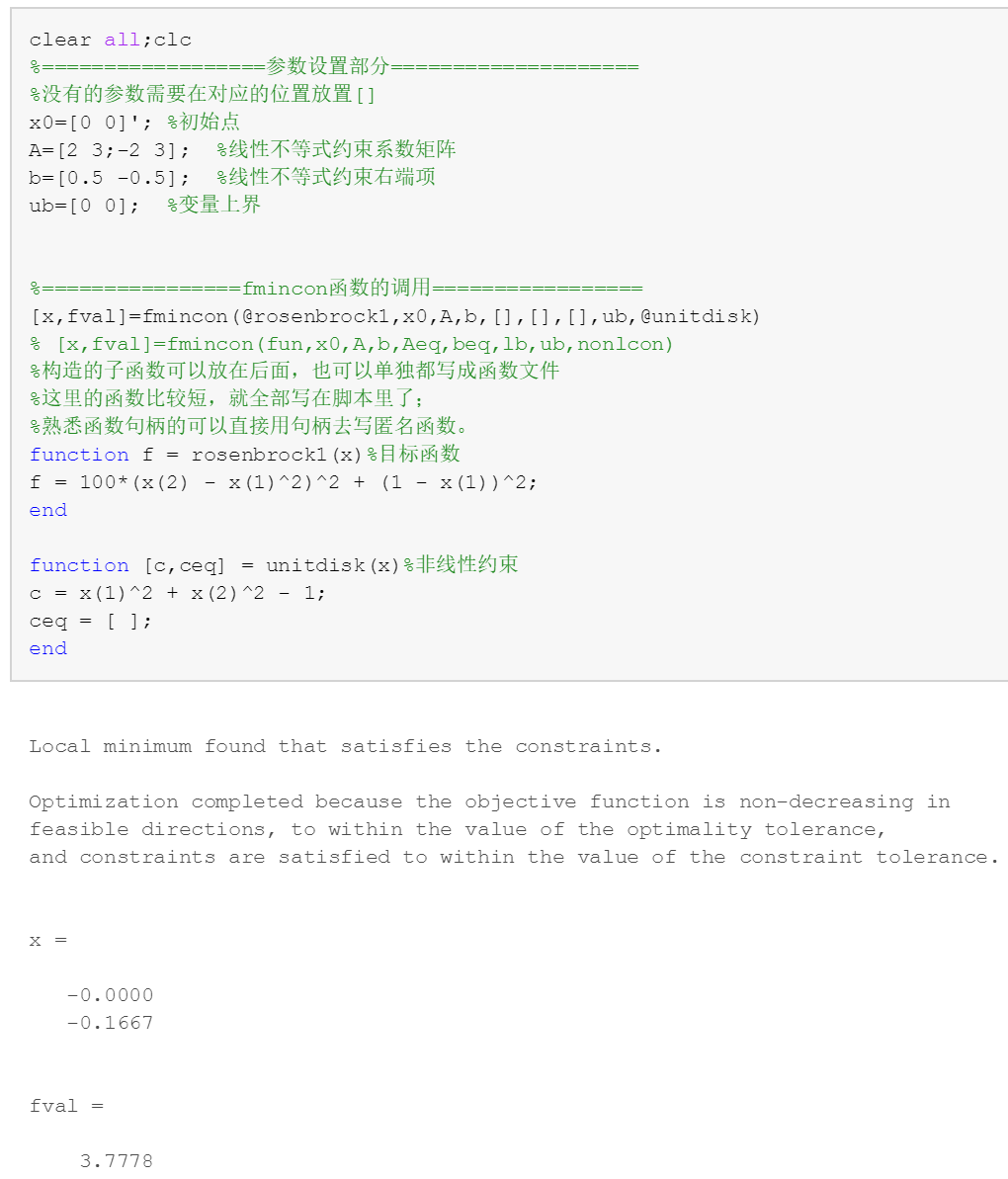
最后完整的代码及结果截图如下(源代码在阅读原文):
fmincon部分最简单的介绍就到此结束了,你学会了吗?

粒子群算法函数
[x, fmin] = particleswarm(fun,nvars,lb,ub)
这个参数看着要少很多,原因是粒子群(PSO)算法是一种启发式算法(具体什么意思自行百度哈)。这里不讲原理,只讲应用。
这里的fun的用法与fmincon中fun完全一致,但是要强调的是此处fun的输入参数必须写成一个行向量,不可以是列向量,也不可以是多个标量,这个要求非常严格的!!!nvars是所传入的列向量的维度,即变量的个数,数一数就知道了。对于上面fmincon中的例子,nvars=2。
(PSO直观示意图,此图来自知乎)
下面看针对fmincon中的例子,采用粒子群算法进行求解的代码怎么写。
首先这里没有地方写约束条件,但是又不可能不考虑约束条件,怎么办?那就把问题转化为无约束问题——具体利用惩罚函数法:
即将几个约束全部纳入目标函数中,构造出新的目标函数g(x),写成如下图形式,其中M是一个非常大的正数(非常大是相对于f(x)而言)。C(x)是一个非负数,当约束条件全部满足时,C(x)=0,否则依赖于不满足的程度而变化,具体的C(x)如下:
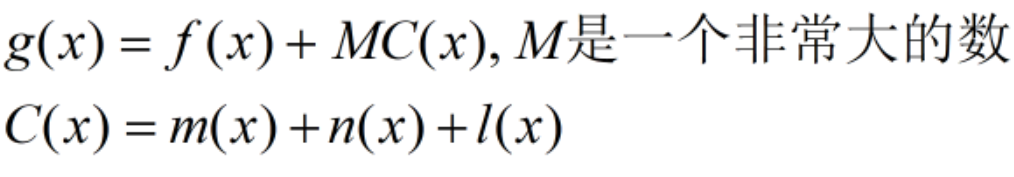
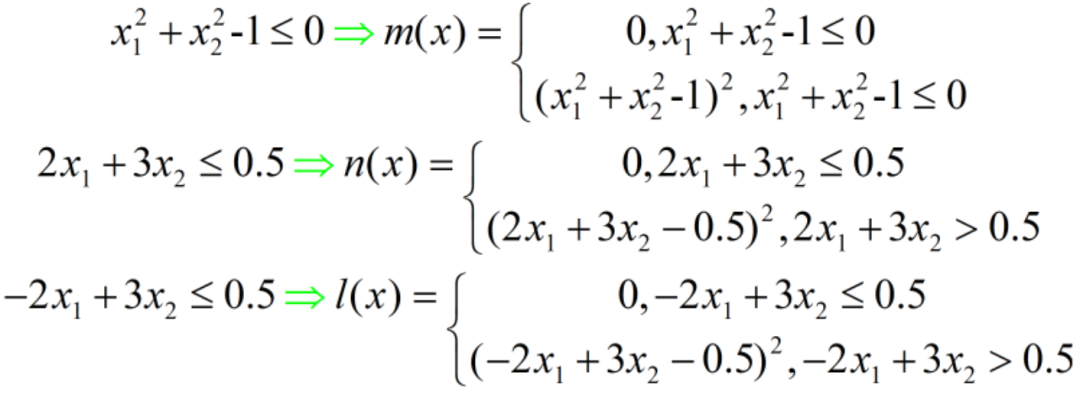
这时就可以尽量保证约束条件的满足,因为当约束条件不满足时(C(x)不等于0),函数值将变得非常大(惩罚),所以优先自动满足约束条件以进行寻优过程。最后来看完整代码:
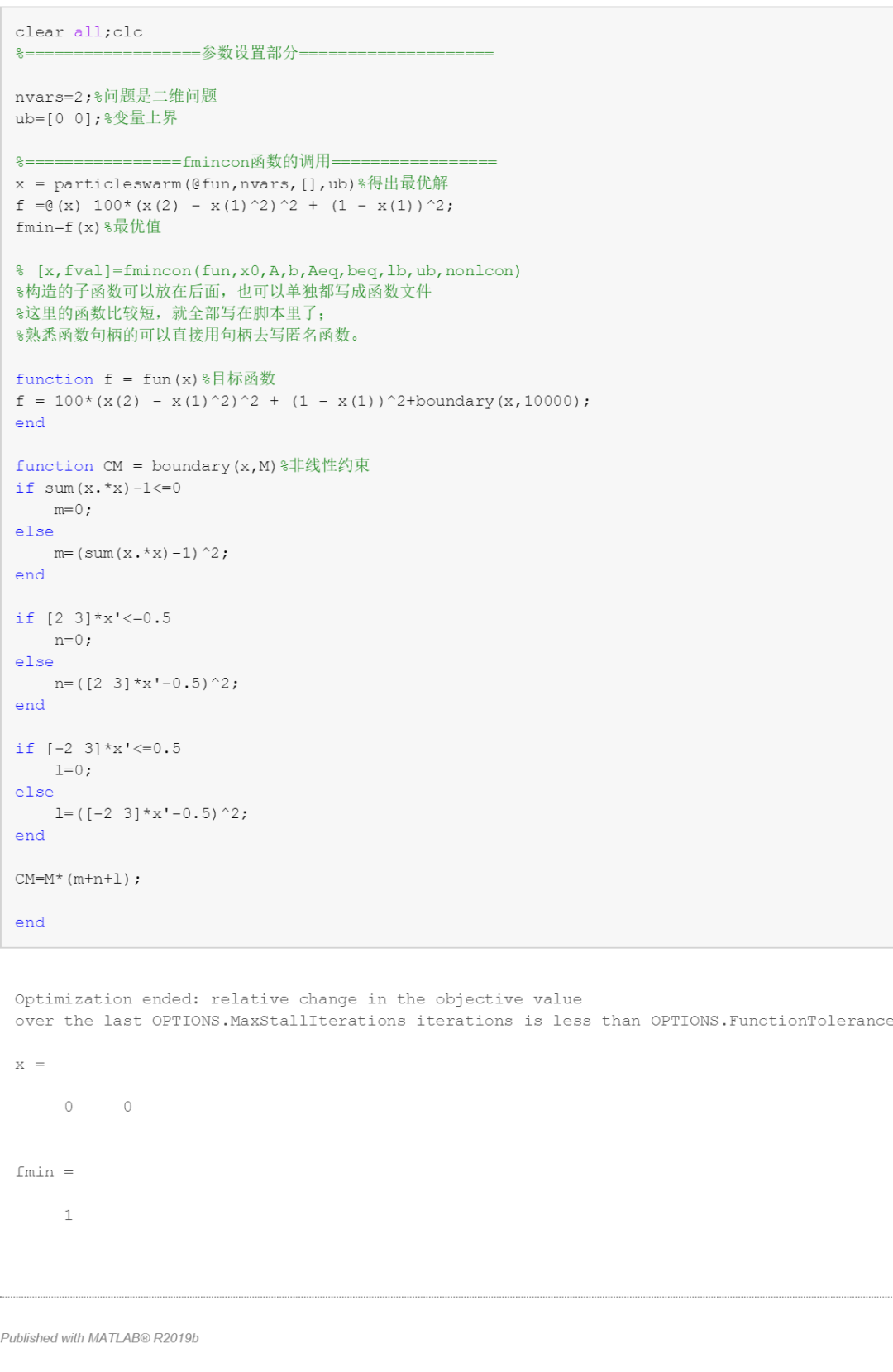
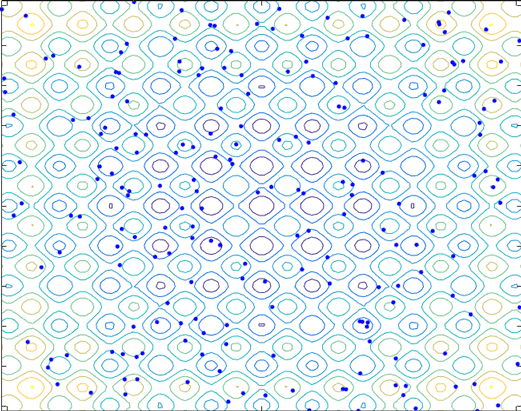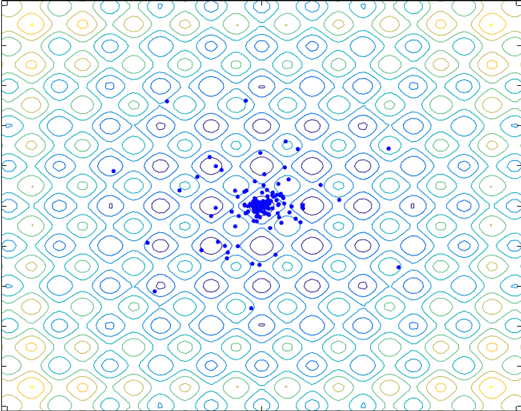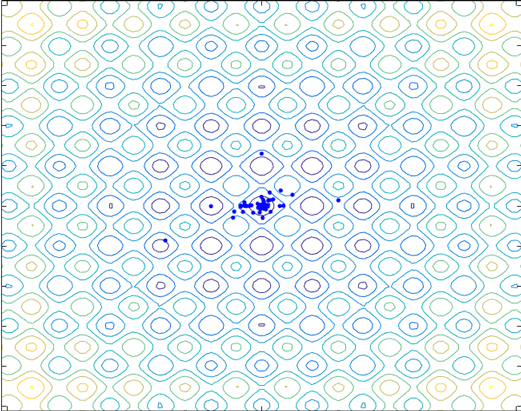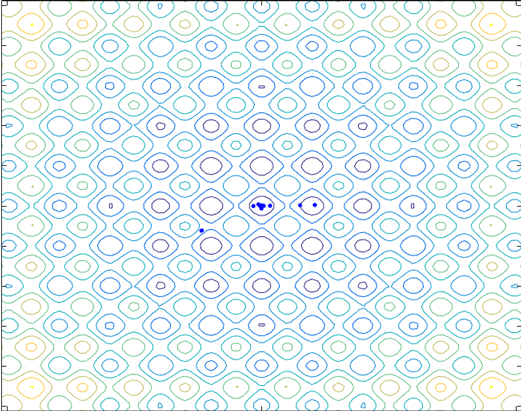
比较两种方法,可以看出,就本问题而言,PSO算法能够找到更好的最优解,但由于其启发式特性,对于复杂问题,每次找到最优解不一定相同。


最后
以上就是沉默铃铛最近收集整理的关于latex不等于_你可能不知道的MATLAB操作#第四话的全部内容,更多相关latex不等于_你可能不知道内容请搜索靠谱客的其他文章。








发表评论 取消回复