作为自学数电的笔记使用
教学视频连接-----清华大学王红–数电教学视频
0.1.数字量和模拟量
数字量:在时间与数量上都是离散的、不连续的。
模拟量:在时间与数量上都是连续的。
数字电子技术基础:所研究的所有对象都是离散的
0.2电子技术的发展历程
电子技术:研究电子器件及电子器件应用的一门学科
电子技术的发展:集成度发展的过程(摩尔定律)
58年 集成电路出现----EDA技术
如何学习:先掌握基本的电路设计方法
采用EDA技术设计电路
电子电路:处理信息,能量转换
模拟电路:用连续的模拟电压/流值来表示信息
数字电路:用一个离散的电压序列来表示信息
课程基本任务
计算机–电路板–芯片–模块–电路单元–逻辑门电路–晶体管
器件+软件 = 完整计算机系统
我们看见什么?
1.结构:分层设计
2.接口:
系统设计原则
- 成本低,功能复杂
- 适应环境
- 对技术升级具有兼容性
课程学习最好结合实践:
- 面包板搭建中小规模电路
- 可编程器件实现大规模电路
- PCB板实现成熟电路
1.1信息和编码
信息:解决不确定性
信息的度量:需要多少位表达事情的发生
log2(M/N)
编码:进行信息表达和处理的开始
例:100084
- 数制: 每一位的构成/从低位到高位的进位规则(位有权值)
例:二进制、八进制、十进制、十六进制
每三位二进制一个八进制
每四位二进制一个六进制
表示小数:权为负 - 码制
1.2二进制数的补码
解决正负相加回0问题
二进制的正、负号也是用0/1表示的
最高位为符号位
补码的表达
- -最高位为符号位 0位正、1为负
- 正数补码与其原码相同
- 负数补码 = 数值位逐位取反 + 1
可表达的范围(共N位)
范围:-2[N-1]~2[N-1]-1
1.3二进制补码表达的符号位
1.清楚知道运算结果位数为多少,运算时对位数即进行扩展
***注意·在电子电路设计之初选择正确的位数大小

1.4二进制的编码
等长编码
常用十进制代码:8421码/余3码/2421码
格雷码:每一位状态循环,按一定顺序
采取合适编码方式编码方式不唯一(二维码)
1.5用电压表示信息
电压表示的优点:
- 易产生,容易测量
- 功耗小
电压表示的缺点: - 易受到环境影响
- 电压信号为直流
- 遇到RC环境,慢
电压表示黑白图像:0-1连续量表示黑-白这样的连续量
拷贝/取反
1.6 电压信号的离散化
我只输出0,1(高质量)
我只接受0,1(可低质量)
数字系统:
(接地)0–非0非1区—1(电源信号)
靠两头高质量
靠中间低质量(区分逻辑上的0和1)
2.1逻辑代数概述
基本内容:
- 逻辑代数
- 基本运算、公式和定理
- 逻辑函数的表示、转换和化简
概述:
逻辑代数:逻辑运算的数学方法
数字电子技术:逻辑代数+二极管
2.2逻辑代数三种基本运算
- 三种基本运算:
与 或 非
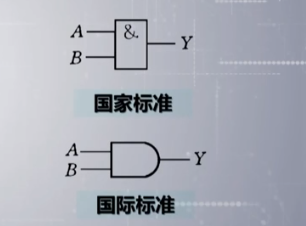
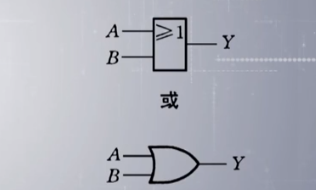
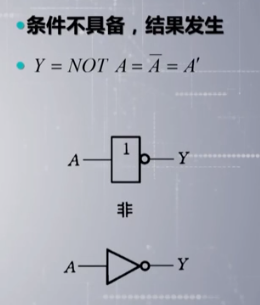
实现非运算的门叫做 非门 或者 叫做 反向器
2.3几种常见的符合逻辑运算
与非/或非/与或非
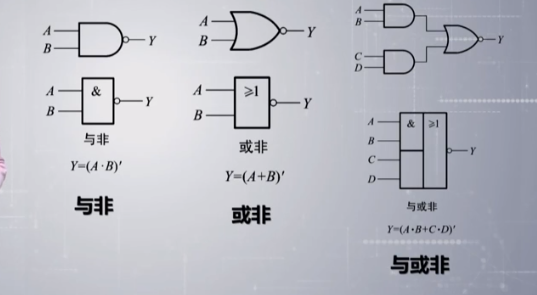
异或:相同则为0,不同则为1
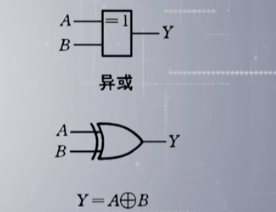
同或: 相同则为1,不同则为0
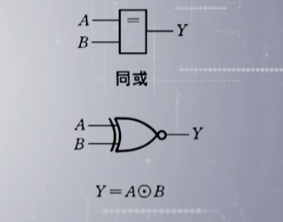
2.4逻辑代数的基本公式和常用公式
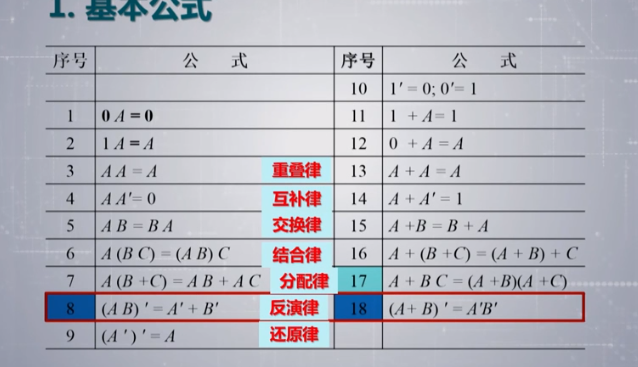
穷举法证明----适用于一切

如何证明5:将BC扩充,扩充为 ABC + A’BC = BC(A+A‘)= BC,再证明
2.5逻辑代数的基本定理
- 代入定理
逻辑电路的互联基础 - 反演定理
Y => Y’
原变量 => 反变量
反变量 => 原变量
与 => 或
或 => 与
0 => 1
1 => 0
注意事项:变换顺序先括号,然后与,最后或
不属于单个变量的上的反号保留不变
3.对偶定理
与 => 或
或 => 与
0 => 1
1 => 0
*若是两式子等价 , 则其对偶式等价
2.6逻辑函数及其表示方法
逻辑函数
表示方法: 1. 真值表
2. 逻辑式
3. 逻辑图(与电路实现相对应)
4. 波形图 (利用示波器等观察输入输出的持续波形)

2.7逻辑函数表示方法之间的转换
1.波形图 -> 真值表
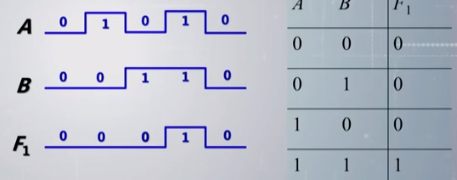
2. 真值表 -> 逻辑式

3. 逻辑式 -> 真值表
4. 逻辑式 -> 逻辑图
5. 逻辑图 -> 逻辑式 (逐级表示)
6. 逻辑式 -> 逻辑式
2.8逻辑函数公式的化简法
- 逻辑式最简形式
1) 包含的与项已经最少
2)每个与项的因子也已经最少 - 公式化简法
化简采用方法不唯一
2.9逻辑函数最小项之和
- 最小项

- 最小项编号
(对应十进制数作为编号) - 最小项性质
- 输入变量任意取值下,有且就有一个最小项的值为1
- 全体最小项之和为1
- 任何两个最小项之积为0
- 两个相邻最小项之和可以合并,消去一对因子
- 与或式 -> 最小项之和(补元)
2.10逻辑函数最大项之积
- 最小项性质
- 输入变量任意取值下,有且就有一个最大项的值为0
- 全体最大项之积为0
- 任何两个最小项之和为1
- 两个相邻最大项之积可以合并,消去一对因子
- 或与式 -> 最大项之积(补元)、
2.11逻辑函数最大项最小项关系
相同编号最小项与最大项互为反函数
最小项之和转换为最大项之积:
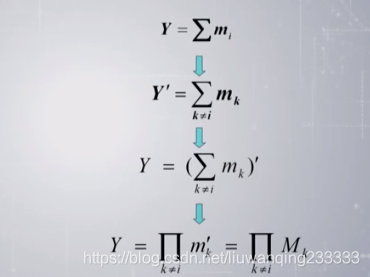
2.12逻辑函数的卡诺图
- 卡诺图定义

- 以五变量卡诺图为例(失去了几何相邻,逻辑相关的特点)
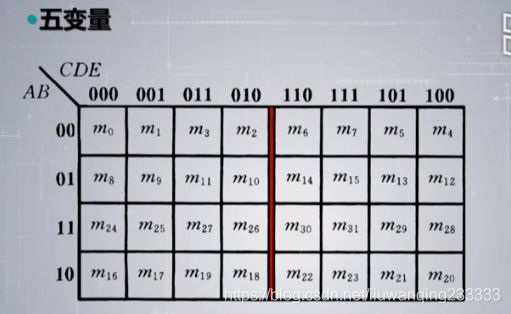
- 用卡诺图表示逻辑函数
将卡诺图表示为最小项之和的形式
在卡诺图使将最小项对应填上1,其余位置填入0 - 简化方案
确定与项为1的所有取值形式,填入即可
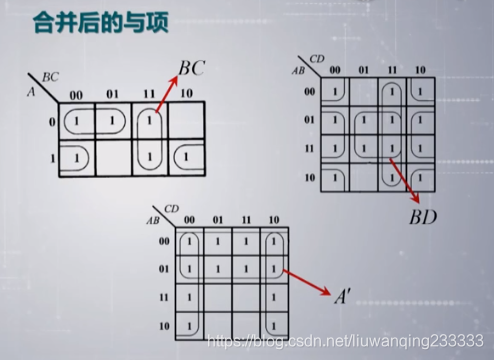
2.13逻辑函数的卡诺图
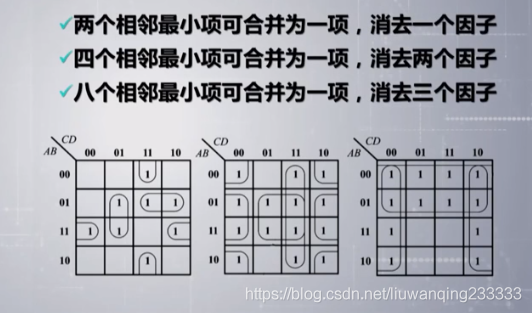
合并后与项例子
跨域的去掉
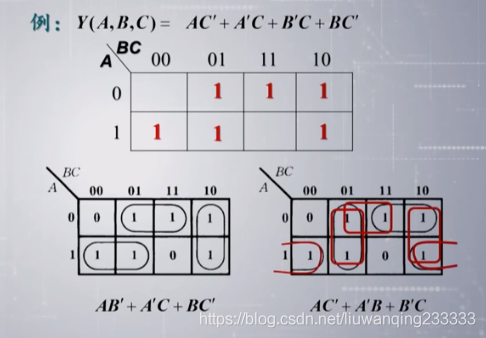
卡诺图化简原则
11. 与项数目最少,即圈成的矩形数最少
12. 保证每个的因子最少,即圈成的矩形最大
13. 每个圈中至少有一个 1, 只被圈过一次, 否则那个圈就是多余的。
例题:
2.14具有无关项的逻辑函数及其化简
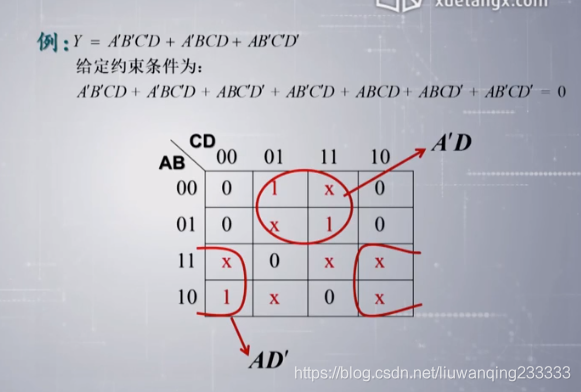
- 无关项(可以写入逻辑式,可以不写入逻辑式):
- 约束项: 逻辑函数中对输入变量的取值有限制,与这些被限制的取值相对应的最小项称为约束项
- 任意项:在输入变量的某项取值下, 函数值为1或0不影响逻辑函数的功能, 这些取值相对应的最小项称为任意项
- 利用无关项进行逻辑函数化简
例子:
最后
以上就是甜蜜睫毛最近收集整理的关于数字电路基础的全部内容,更多相关数字电路基础内容请搜索靠谱客的其他文章。








发表评论 取消回复