概述
文章目录
- 1. 逻辑函数的描述方法
- 1.1 真值表
- 1.2 逻辑函数式
- 1.2.1 逻辑代数的基本公式和常用公式
- 1.3 逻辑图
- 1.4 波形图
- 2. 各种描述之间的转换方法解析
- 一，波形图转化为真值表：
- 二，真值表得到逻辑表达式
- 三，由逻辑表达式得到波形图
1. 逻辑函数的描述方法
1.1 真值表
概念：表征逻辑事件输入和输出之间全部可能状态的表格。列出命题公式真假值的表。通常以1表示真，0 表示假
下面我们来看一张真值表：
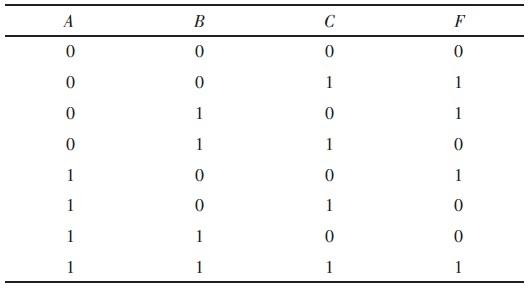
A,B,C表示输入，F表示输出
通常我们在写真值表的时候，最好是按照一定的排列组合顺序把输入变量所有取值写出来，再根据电路或者其他方式看看输出情况。这样可以避免遗漏或者重复
1.2 逻辑函数式
这些概念其实是很好理解的，所谓逻辑函数式，也就是将输入和输出之间的逻辑关系写成与，或，非等运算的组合式，举个例子：Y = A（B + C） ；这就是一个逻辑函数式
1.2.1 逻辑代数的基本公式和常用公式
这里我们可能是已知逻辑函数式，需要通过不同的0或1的输入判断输出的Y是0还是1，这有时候需要我们对逻辑函数式进行一定的化简，下面我们插入逻辑代数的基本公式和常用公式，以便日后复习使用：（博主只是记录了部分较重要的）
| 序号 | 公式 |
|---|---|
| 1 | 0 • A = 0 quadquadquadquad 0•A = 0 quadquadquadquad 0•A=0 |
| 2 | 1 • A = 1 quadquadquadquad 1•A = 1 quadquadquadquad 1•A=1 |
| 3 | A • A = A quadquadquadquad A•A = A quadquadquadquad A•A=A |
| 4 | A ′ • A = 0 quadquadquadquad A'•A = 0 quadquadquadquad A′•A=0 |
| 5 | A • ( B + C ) = A • B + A • C quadquadquadquad A•(B + C) = A • B + A • C quadquad A•(B+C)=A•B+A•C |
| 6 | A • ( B • C ) = ( A • B ) • C quadquadquadquad A • (B•C) = (A•B) • C quadquad A•(B•C)=(A•B)•C |
| 7 | ( A • B ) ′ = A ′ + B ′ quadquadquadquad (A•B)' = A' + B' quadquadquadquad (A•B)′=A′+B′ |
| 8 | ( A ′ ) ′ = A quadquadquadquad (A')' = A quadquadquadquad (A′)′=A |
| 9 | 1 + A = A ; 0 + A = A ; A + A = A ; A + A ′ = 1 quadquadquadquad 1 + A = A; quad0 + A = A; quad A + A = A; quad A + A' = 1quadquadquad 1+A=A;0+A=A;A+A=A;A+A′=1 |
| 10 | ( A + B ) ′ = A ′ • B ′ quadquadquadquad (A+B)' = A' • B' quadquadquadquad (A+B)′=A′•B′ |
| 11 | A + A • B = A quadquadquadquad A + A• B = A quadquadquadquad A+A•B=A |
| 12 | A + A ′ • B = A + B quadquadquadquad A + A'• B = A + B quadquadquadquad A+A′•B=A+B |
| 13 | A • ( A + B ) = A quadquadquadquad A • (A + B) = A quadquadquad A•(A+B)=A |
| 14 | A • B + A • B ′ = A quadquadquadquad A • B + A • B' = A quadquadquad A•B+A•B′=A |
1.3 逻辑图
逻辑图就是将逻辑函数式中各个变量之间与，或，非等逻辑关系用图形表示出来
下面我们来复习一下两套表示与，或，非的符号：
而由与，或，非还能组成另一些复合逻辑：与非，或非，与或非，同或，异或
- 与非：Y = (AB)’ 顾名思义，先将两个输入做“与”运算，在将与运算的结果取反
- 或非：Y = (A+B)’ 类似，先做或运算，在做非运算
- 与或非：Y = (AB + CD)’ 与或非逻辑一般有4个输入，我们将他们两两为一组，先对每组进行与运算，再将两组与运算得到的结果进行或运算，最后再将得到的结果进行取反
- 同或：Y = A ⊕ B 相同为真“1”，不同为假“0”
- 异或：Y = A ⊙ B 相同为假“0”，不同为真“1”
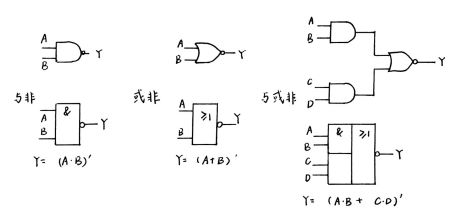
这些逻辑符号的不同组合就能够得到我们的逻辑图啦
1.4 波形图
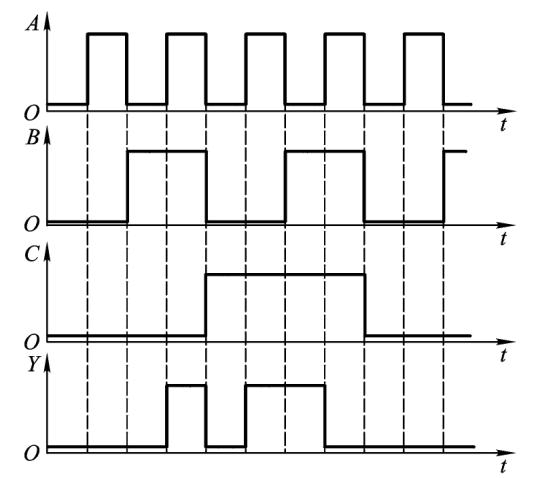
将逻辑函数输入变量每一种可能出现的取值与对应的输出值按时间顺序依次排列起来，就得到了描述该逻辑函数的波形图，也成为“时序图”。我们看看下面的例子：
2. 各种描述之间的转换方法解析
一，波形图转化为真值表：
这个比较简单，首先，我们先把输入的所有排列组合的情况先列出来，然后再根据输入组合的情况依次在波形图中找到对应的Y，并且填入真值表中
以上面的波形图为例：我们先写出输出A,B,C所有的组合情况：
| A | B | C | Y |
|---|---|---|---|
| 0 | 0 | 0 | |
| 0 | 1 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
接下来，就是根据上面不同A,B,C的组合找到对应的Y
| A | B | C | Y |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
二，真值表得到逻辑表达式
这里有一个技巧：首先，我们找到真值表上输出为1的所有组合（以上表为例）
那么，在上表中，Y为1的所有输入组合分别为：（011，101，110）
然后，每一组输入变量取值的组合对应一个乘积项，其中，取值为1的写入原变量，取值为0的写入反变量
最后，将这些乘积项相加，得到逻辑表达式
比如011的组合就写成：A’BC；101的组合写成：AB’C；110的组合写成：ABC’
因此，该真值表对应的逻辑表达式为：Y = A’BC + AB’C + ABC’
这里用到的知识是逻辑函数的标准形式，我们在后面的博文中会对它进行记录
三，由逻辑表达式得到波形图
这个是最简单的，直接将每一个取值画出来就OK
最后
以上就是追寻帽子为你收集整理的【数字电子技术 Digital Electronic Technology 2】—— 逻辑代数基础 之 逻辑函数以其描述方法解析1. 逻辑函数的描述方法1.2 逻辑函数式2. 各种描述之间的转换方法解析的全部内容，希望文章能够帮你解决【数字电子技术 Digital Electronic Technology 2】—— 逻辑代数基础 之 逻辑函数以其描述方法解析1. 逻辑函数的描述方法1.2 逻辑函数式2. 各种描述之间的转换方法解析所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复