TI AWR1642毫米波雷达学习笔记之理论基础（3）

101 阅读 0 评论 67 点赞

我是靠谱客的博主大气秋天，最近开发中收集的这篇文章主要介绍TI AWR1642毫米波雷达学习笔记之理论基础（3），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

背景：在前面两篇对于雷达数学模型的讲解和对原始数据排列格式整理后，本文开始对整理后的雷达原始数据进行1D FFT和2D FFT处理以及讲解该步骤的意义是什么。

首先我们需要理解1D FFT和2D FFT其实就是对快时间维和慢时间维数据进行处理，首先对数据进行加窗，然后进行傅里叶变化。

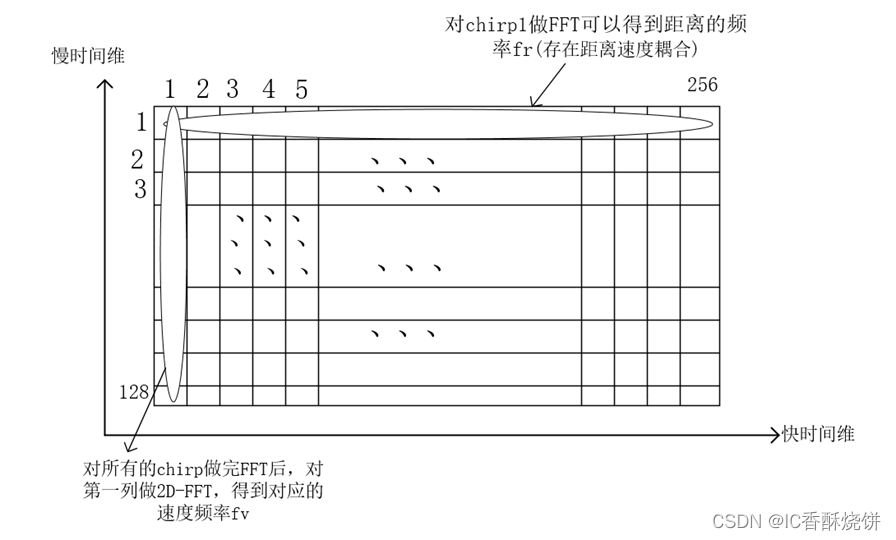
在这里插入图片描述

这里数据格式在前面处理后为天线维X快时间维X慢时间维的三维矩阵，这里天线维为8（发射天线数X接收天线数），快时间维主要与参数 ADC samples 有关，这里本文设置为256，慢时间维与参数中设置的chrip数有关，这里设置的为128。所以综上所述，雷达数据三维矩阵其实为8X256X128的数据矩阵。上图即为将数据从天线维方向横切，剩下快时间维和慢时间维的二维矩阵，雷达信号处理都是基于快时间维X慢时间维的处理。由于1D FFT和2D FFT原理相同，只是处理对象不一样，一个是对快维数据进行处理得到距离信息，一个是对慢时间维处理得到速度信息。MATLAB示例代码如下：

function [frameRange] = rangeFFT(frameSample,isAddWin,isRmClutter)
%对一帧的采样数据进行距离FFT

%frameSample ：输入数据，一个三维数组：天线高维*chirps行维*samples列维
%frameRange ： 输出

[numAnt,chirpsPerFrame,samplesPerChirp] = size(frameSample);
frameRange = zeros(numAnt,chirpsPerFrame,samplesPerChirp);

 winFun = (hann(samplesPerChirp))';
 
for ii=1:numAnt
    oneAntData = squeeze(frameSample(ii,:,:));   %删除单一维度数据，构建一个numChirp*numSample的二维数据并赋值
    if(isAddWin==1)
         oneAntData = oneAntData.*winFun; %加窗
    end      
      
 
    
    rangeData =fft(oneAntData, samplesPerChirp, 2);  %2表示对行做FFT
    rangeData=fftshift(rangeData);
    if(isRmClutter==1)
        sumFFT = sum(rangeData,1)/chirpsPerFrame; %静态杂波滤除    %sum每一行的采样点积累后求平均
        frameRange(ii,:,:) = rangeData - sumFFT;       
    else
        frameRange(ii,:,:) = rangeData;
    end
end

end

在1D FFT 和2D FFT 后的雷达信号图如下：

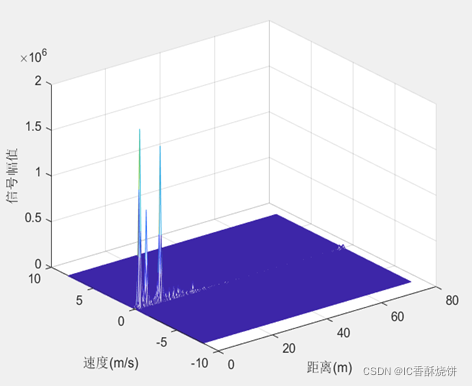
在这里插入图片描述

在进行FFT过程中，需要对数据进行加窗函数。一般来说实际信号是有限长且连续的，当使用快速傅里叶变换时会将连续的信号截取一部分，然后再不断重复成无限长的信号从而方便进行处理，当频谱截取不当时，连续信号的边缘有可能会出现波形不连续的情况，这种情况会导致频谱泄漏的发生，从而导致最后测得的频率跟实际频率有所差别。为了防止这种现象发生可以通过对信号进行加窗使得波形不连续的边缘变得平滑，这样可以降低快速傅里叶变换产生的频谱泄漏。
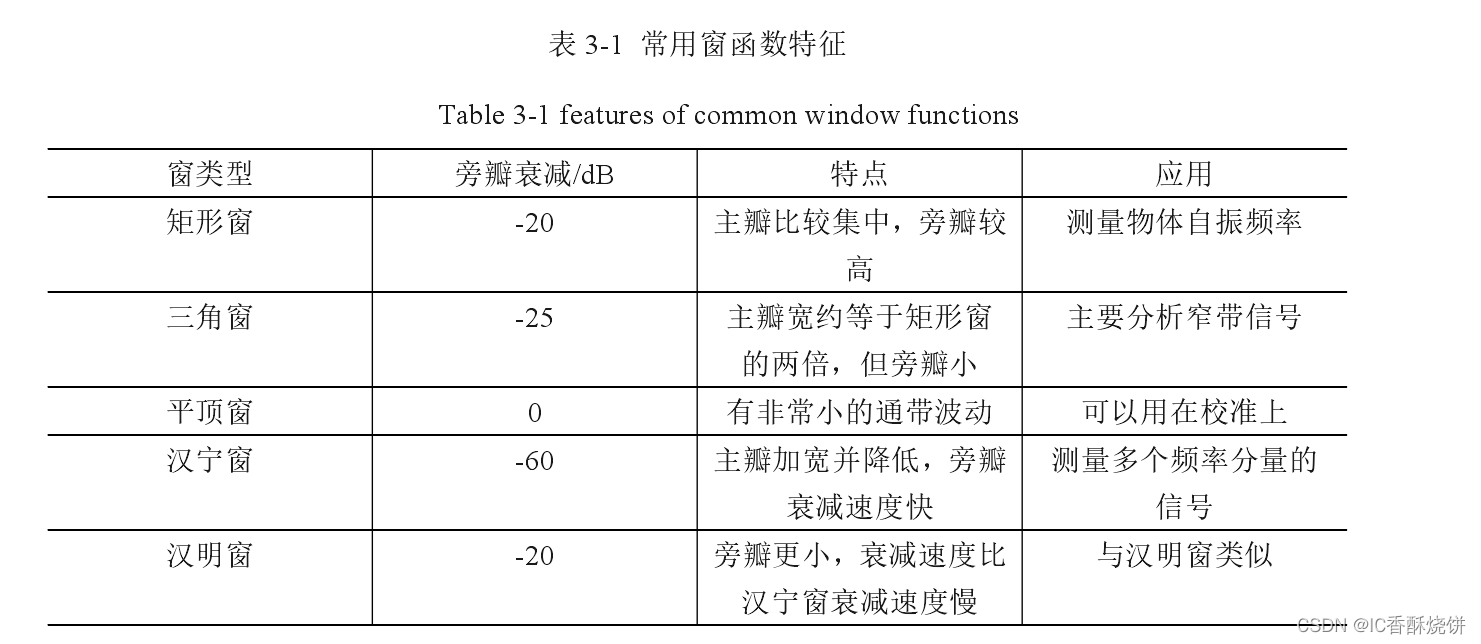
在这里插入图片描述