雷达原理笔记之动目标检测及测速技术
——南京理工大学许志勇老师的《雷达原理课程》浅析
文章目录
- 雷达原理笔记之动目标检测及测速技术
- 1.杂波对消处理
- 1.1任务
- 1.2一次杂波对消器：
- 1.3二次杂波对消器
- 2多普勒滤波器组处理
- 2.1窄带多普勒滤波器组实现
- 3.附录
- 3.1一次相消器图片matlab代码
- 3.2二次相消器图片matlab代码
- 3.3二次相消器图片（静止、运动杂波）matlab代码
- 3.4多普勒滤波器组频响matlab代码
动目标检测技术主要包括MTI杂波对消处理以及MTD窄带多普勒滤波组滤波处理。本文主要介绍这两个方面的实现原理及过程。
1.杂波对消处理
雷达检测目标常常是在强杂波背景中进行，信杂比非常小。这对目标探测很不利。考虑到杂波频谱通常比较稳定，大多在零多普勒附近，由此引出消除固定、低速杂波的滤波器——杂波对消器。
1.1任务
- 抑制固定杂波以及低速杂波，进而提取运动目标信息。
1.2一次杂波对消器：
y [ n ] = x [ n ] − α x [ n − 1 ] y[n]=x[n]-alpha x[n-1] y[n]=x[n]−αx[n−1]
滤波器频率特性：
H
(
z
)
=
1
−
α
z
−
1
H(z)=1-alpha z^{-1}
H(z)=1−αz−1
其中
α
alpha
α通常取接近1但小于1的常数。目的是保证尽可能多地滤除杂波的同时，处在零多普勒点的运动目标不被抑制完全。对比见下图：
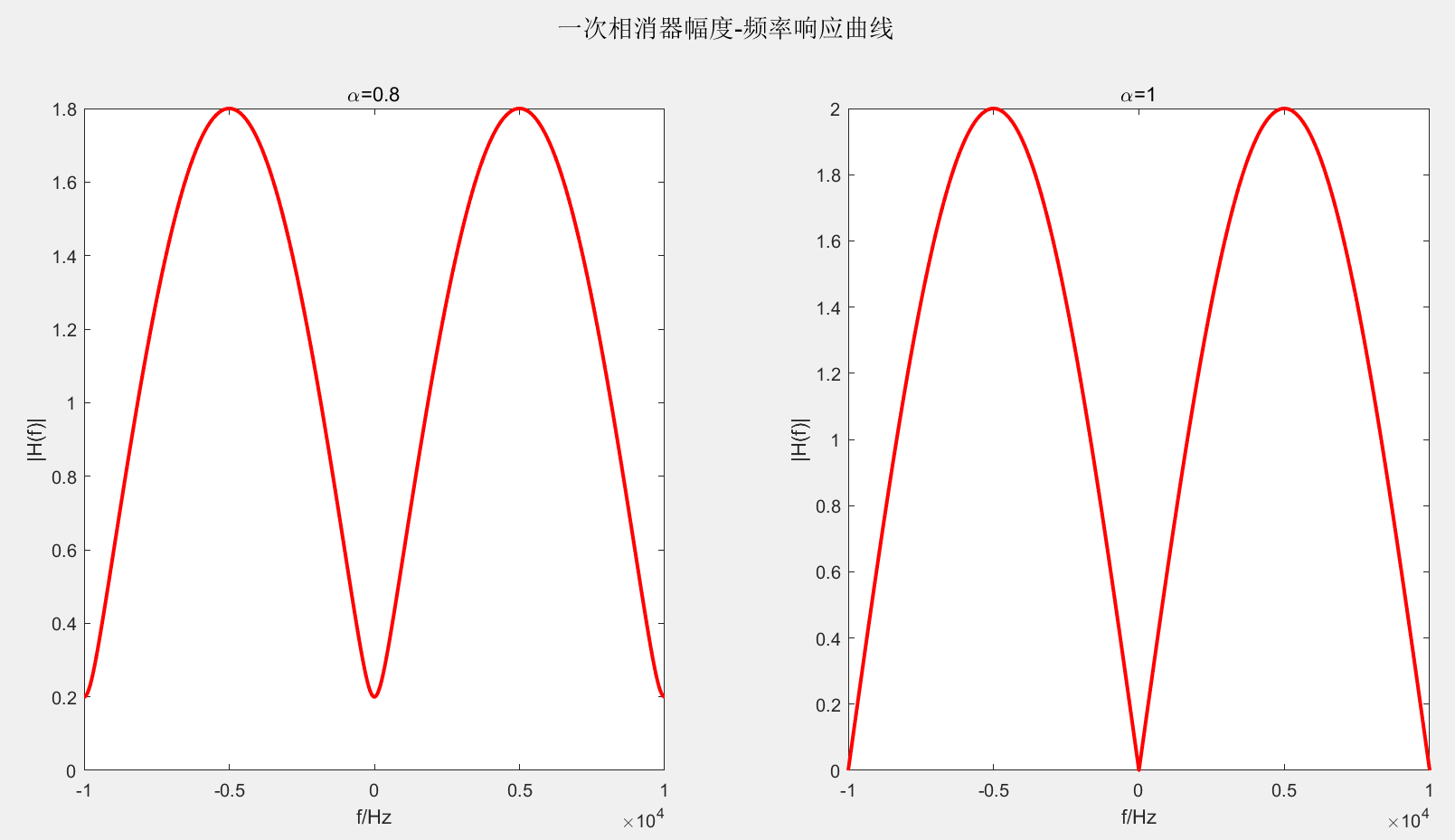
1.3二次杂波对消器
y [ n ] = x [ n ] − α x [ n − 1 ] + x [ n − 2 ] y[n]=x[n]-alpha x[n-1]+x[n-2] y[n]=x[n]−αx[n−1]+x[n−2]
滤波器频率特性：
H
(
z
)
=
1
−
α
z
−
1
+
z
−
2
H(z)=1-alpha z^{-1}+z^{-2}
H(z)=1−αz−1+z−2
其中
α
alpha
α通常取接近2但小于2的常数。目的同样是在保证尽可能多地滤除杂波的同时，处在零多普勒点的运动目标不被抑制完全。对比见下图：
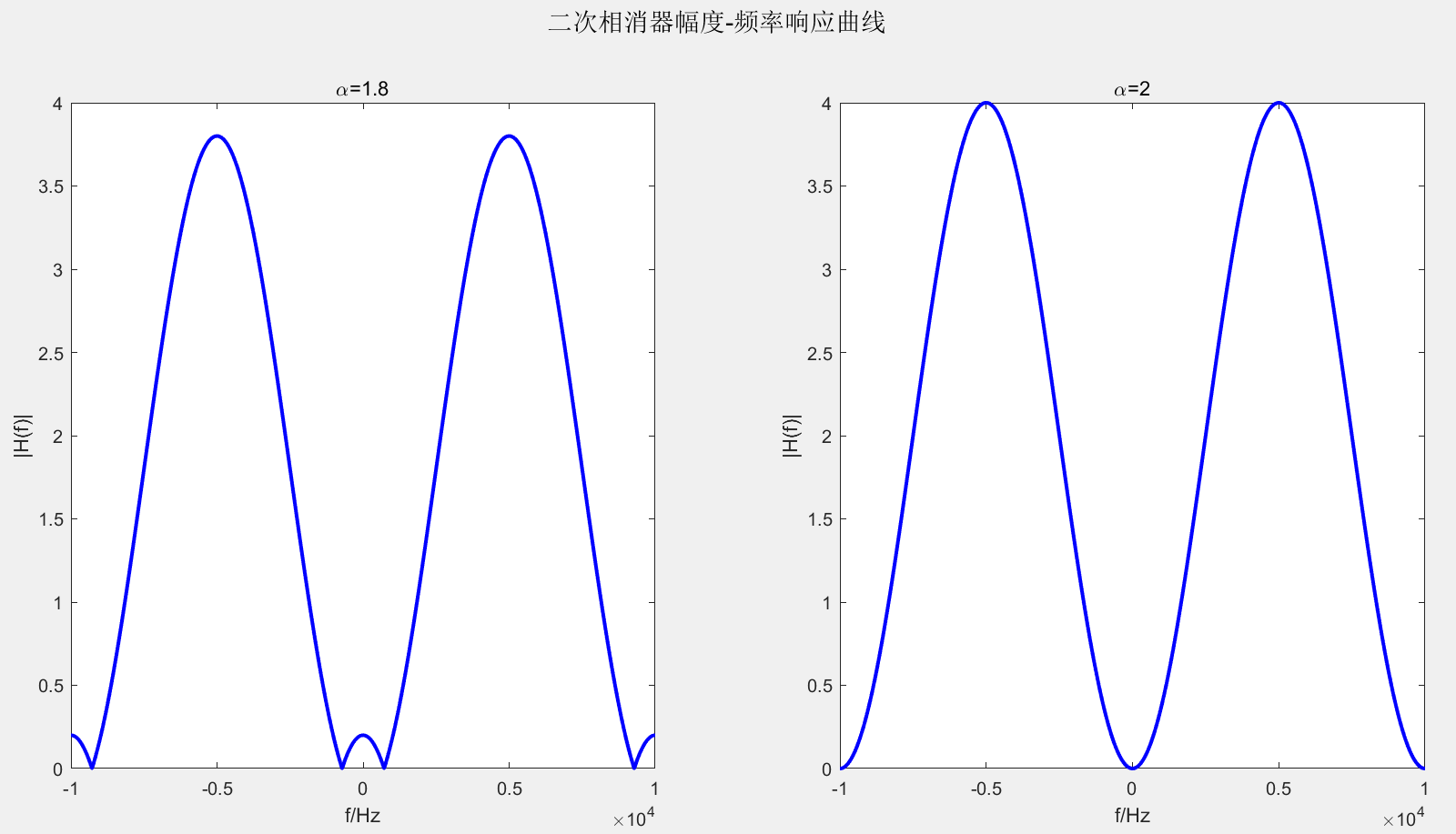
二次杂波对消器是工程中应用最多的杂波处理滤波器。对于低速的杂波消除，频响特性可以向右平移一定的区间，平移的量是杂波运动速度对应的多普勒频移。因此对于低速运动杂波对消的滤波特性为：
H
(
z
)
=
1
−
α
e
j
β
z
−
1
+
e
j
2
β
z
−
2
H(z)=1-alpha e^{jbeta}z^{-1}+e^{j2beta}z^{-2}
H(z)=1−αejβz−1+ej2βz−2
其中
β
beta
β为杂波速度对应的多普勒频移。
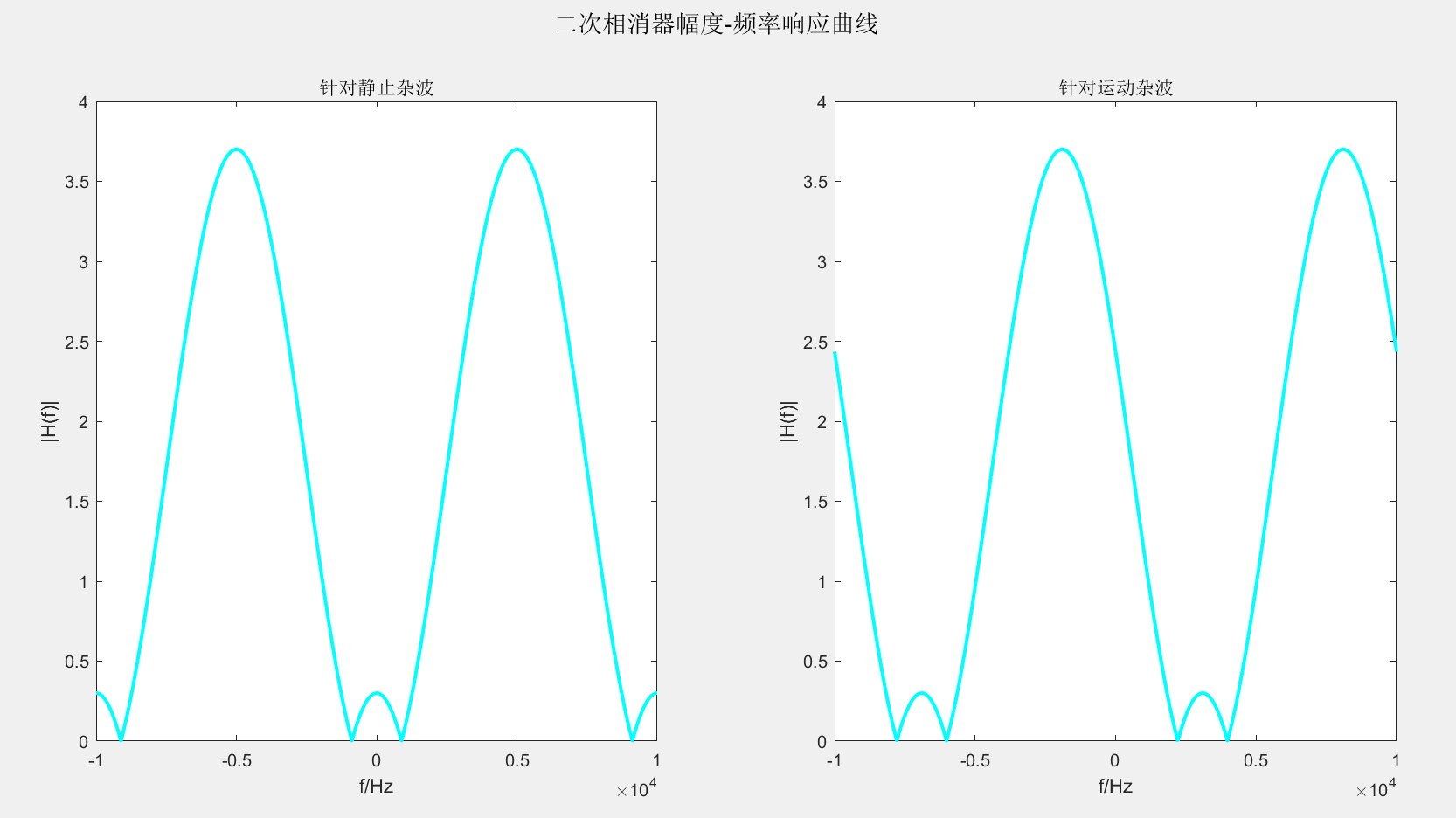
利用二次杂波对消器处理杂波时，选取相参积累脉冲个数为 K = 2 N + 2 K=2^N+2 K=2N+2。
2多普勒滤波器组处理
一般，将MTI处理后输出的信号进行MTD处理，即窄带滤波处理，得到运动目标的速度信息。
2.1窄带多普勒滤波器组实现
利用有N个输出的横向滤波器，经过各脉冲的加权求和实现。
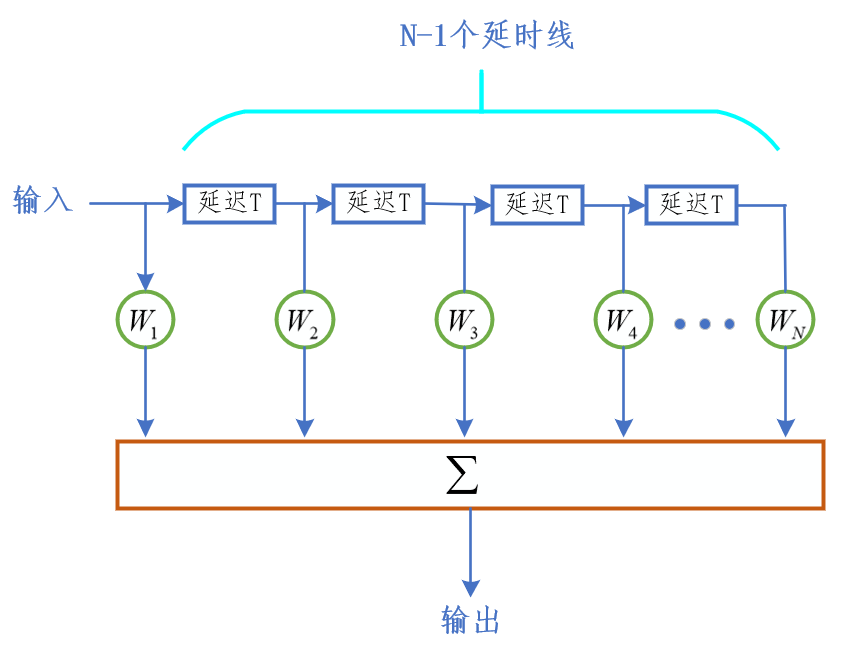
每根延时线延迟时间
T
=
1
/
P
R
F
T=1/PRF
T=1/PRF。每个窄带滤波器输出的频率响应为：
H
k
(
f
)
=
e
−
j
2
π
f
t
∑
i
=
1
N
e
−
j
2
π
(
i
−
1
)
[
f
T
−
k
/
N
]
H_k(f)=e^{-j2pi ft}sum_{i=1}^{N}e^{-j2pi (i-1)[fT-k/N]}
Hk(f)=e−j2πfti=1∑Ne−j2π(i−1)[fT−k/N]
频响幅度为：
∣
H
k
(
f
)
∣
=
s
i
n
[
π
N
(
f
T
−
k
/
N
)
]
s
i
n
[
π
(
f
T
−
k
/
N
)
]
|H_k(f)|=frac{sin[pi N(fT-k/N)]}{sin[pi (fT-k/N)]}
∣Hk(f)∣=sin[π(fT−k/N)]sin[πN(fT−k/N)]
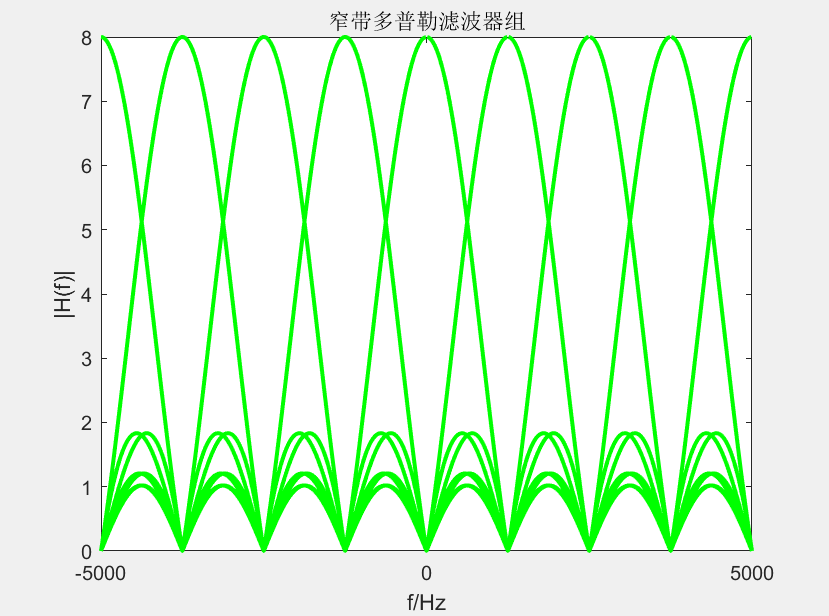
上图所示的多普勒滤波器组，对应的发射信号脉冲重复频率为10kHz。其覆盖整个多普勒频谱周期
[
−
5000
H
z
,
5000
H
z
]
[-5000Hz,5000Hz]
[−5000Hz,5000Hz]。这个周期称作是多普勒滤波器组的主周期。此滤波器组长度N=8。每个窄带滤波器中心频率满足：
f
=
5000
k
/
N
(
H
z
)
(
N
=
8
,
k
=
−
4
,
−
3
,
…
4
)
f=5000k/N(Hz)quad (N=8,k=-4,-3,…4)
f=5000k/N(Hz)(N=8,k=−4,−3,…4)
若某运动目标的频谱出现在其中一个滤波器中，则该滤波器的中心频率对应的频率即为运动目标
f
d
f_d
fd的估值。
当然，N取值越大对应的滤波器组间隔越小，运动目标的 f d f_d fd的估值越接近真实值。
利用多普勒滤波器组实现相参积累，可以将白噪声背景中信号的信噪比提高N倍。
3.附录
3.1一次相消器图片matlab代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24clc close all clearvars a=0.8; T=1e-4;%发射信号周期 f=-1/T:10:1/T;%频率轴 w=2*pi*f;%角频率 z=exp(1j*w*T);%映射到z轴 H=1-a*z.^(-1);%滤波器传输函数表达式（针对静止杂波） figure subplot(1,2,1) plot(f,(abs(H)),'r-','LineWidth',2); title('alpha=0.8') xlabel('f/Hz') ylabel('|H(f)|') subplot(1,2,2) a=1; H=1-a*z.^(-1);%滤波器传输函数表达式（针对运动杂波） plot(f,(abs(H)),'r-','LineWidth',2); title('alpha=1') xlabel('f/Hz') ylabel('|H(f)|') suptitle('一次相消器幅度-频率响应曲线')
3.2二次相消器图片matlab代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24clc close all clearvars a=1.8; T=1e-4;%发射信号周期 f=-1/T:10:1/T;%频率轴 w=2*pi*f;%角频率 z=exp(1j*w*T);%映射到z轴 H=1-a*z.^(-1)+z.^(-2);%滤波器传输函数表达式（针对静止杂波） figure subplot(1,2,1) plot(f,(abs(H)),'b-','LineWidth',2); title('alpha=1.8') xlabel('f/Hz') ylabel('|H(f)|') subplot(1,2,2) a=2; H=1-a*z.^(-1)+z.^(-2);%滤波器传输函数表达式（针对运动杂波） plot(f,(abs(H)),'b-','LineWidth',2); title('alpha=2') xlabel('f/Hz') ylabel('|H(f)|') suptitle('二次相消器幅度-频率响应曲线')
3.3二次相消器图片（静止、运动杂波）matlab代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25clc close all clearvars k=1.7; T=1e-4;%发射信号周期 f=-1/T:10:1/T;%频率轴 w=2*pi*f;%角频率 z=exp(1j*w*T);%映射到z轴 H=1-k*z.^(-1)+z.^(-2);%滤波器传输函数表达式（针对静止杂波） figure subplot(1,2,1) plot(f,(abs(H)),'c-','LineWidth',2); title('针对静止杂波') xlabel('f/Hz') ylabel('|H(f)|') subplot(1,2,2) b=0.2*1/T;%平移量0.2倍的频谱周期 z1=exp(-1j*b)*z;%加上平移 H=1-k*z1.^(-1)+z1.^(-2);%滤波器传输函数表达式（针对运动杂波） plot(f,(abs(H)),'c-','LineWidth',2); title('针对运动杂波') xlabel('f/Hz') ylabel('|H(f)|') suptitle('二次相消器幅度-频率响应曲线')
3.4多普勒滤波器组频响matlab代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15clc close all clearvars N=8; T=1e-4;%发射信号周期 f=-0.5/T:10:0.5/T;%频率轴 for k=0:N-1 H=(sin(pi*N*(f*T-k/N)))./(sin(pi*(f*T-k/N)));%滤波器传输函数表达式（针对静止杂波） plot(f,abs(H),'g-','LineWidth',2); hold on end title('窄带多普勒滤波器组') xlabel('f/Hz') ylabel('|H(f)|')
最后
以上就是土豪银耳汤最近收集整理的关于雷达原理之动目标检测及测速技术雷达原理笔记之动目标检测及测速技术的全部内容，更多相关雷达原理之动目标检测及测速技术雷达原理笔记之动目标检测及测速技术内容请搜索靠谱客的其他文章。
发表评论 取消回复