1. 集合定义
集合没有精确的数学定义
理解:由离散个体构成的整体称为集合,称这些个体为集合的元素
常见的数集:N, Z, Q, R, C 等分别表示自然数、整数、有理数、实数、复数集合
2. 集合表示法
枚举法----通过列出全体元素来表示集合
谓词表示法----通过谓词概括集合元素的性质
实例:枚举法:自然数集合 N={0,1,2,3,…} 谓词法:S={ x | x是实数,x-1=0}
i. 集合的元素具有的性质
无序性:元素列出的顺序无关
相异性:集合的每个元素只计数一次
确定性:对任何元素和集合都能确定这个元素是否为该集合的元素
任意性:集合的元素也可以是集合
ii.元素与集合的关系隶属关系:或者
集合与集合之间的关系:, =, ⊈, , ,
定义6.1 A B x ( xA xB )
定义6.2 A = B A B B A
定义6.3 A B A B A B
A ⊈ B x ( xA xB )
定义6.4 空集 :不含有任何元素的集合 实例: { x | xR x2+1=0 }
定理6.1 空集是任何集合的子集。 推论 是惟一的
定义6.5 幂集:给定集合A,由集合A的所有子集为元素组成的集合,称为集合A的幂集,记为P(A)(或2A)。幂集的符号化表示为P(A)={ x | x A }
实例:P()={}, P({})={,{}}
计数:如果 |A|=n,则 |P(A)|=2n.
定义6.6 全集 E:包含了所有集合的集合
全集具有相对性:与问题有关,不存在绝对的全集
外延公理 两个集合A与B相等当且仅当其元素相同,记作A = B。
平凡子集 任意一个非空集合A至少有两个子集,一个是空集Æ,另一个是它本身A,称为A的平凡子集。
定义 以集合为元素的集合称为集族。
定义3.8 给定集合A,由集合A的子集为元素组成的集合,称为集合A的子集族。A的所有子集族都是其幂集P(A)的子集。
初级运算,集合的基本运算有
定义6.7 并 AB = {x | xA xB}
交 AB = {x | xA xB}
相对补 AB = {x | xA xB}
定义6.8 对称差 AB = (AB)(BA)
定义6.9 绝对补 A = EA
并和交运算可以推广到有穷个集合上,即
A1 A2 … An = { x | xA1xA2 …xAn}
A1 A2 … An = { x | xA1 xA2 … xAn}
定义6.10 广义并 A = { x | z ( zA xz )}
广义交 A= { x | z ( zA xz )}
广义运算的性质
(1) =,无意义
(2) 单元集{x}的广义并和广义交都等于x
(3) 广义运算减少集合的层次(括弧减少一层)
(4) 广义运算的计算:一般情况下可以转变成初级运算
{A1, A2, … , An}=A1A2…An
{A1, A2, … , An}=A1A2…An
运算优先级的确定
1 类运算:初级运算È, , , ,
优先顺序由括号确定
2 类运算:广义运算和运算,
运算由右向左进行
混合运算:2 类运算优先于1 类运算
有穷集合元素的计数
1. 文氏图法
2. 包含排斥原理
定理6.2 设集合S上定义了n条性质,其中具有第 i 条性质的
元素构成子集Ai, 那么集合中不具有任何性质的元素数为
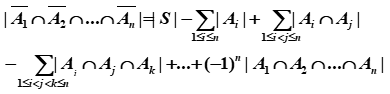
推论 S中至少具有一条性质的元素数为
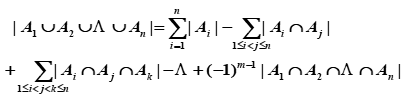
集合恒等式
集合算律
1.只涉及一个运算的算律:
交换律、结合律、幂等律
| | | |
交换 | AB=BA | AB=BA | AB=BA |
结合 | (AB)C =A(BC) | (AB)C= A(BC) | (AB)C =A(BC) |
幂等 | AA=A | AA=A |
|
2.涉及两个不同运算的算律:
分配律、吸收律
| 与 | 与 |
分配 | A(BC)= (AB)(AC) A(BC)= (AB)(AC) | A(BC) =(AB)(AC) |
吸收 | A(AB)=A A(AB)=A |
|
3.涉及补运算的算律:
DM律,双重否定
| | |
D.M律 | A(BC)=(AB)(AC) A(BC)=(AB)(AC) | (BC)=BC (BC)=BC |
双重否定 |
| A=A |
4.涉及全集和空集的算律:
补元律、零律、同一律、否定律
| | E |
补元律 | AA= | AA=E |
零律 | A= | AE=E |
同一律 | A=A | AE=A |
否定 | =E | E= |
定理3.6 设A, B, C为任意的集合,集合运算满足以下所列规律。
(1)双重否定律 ~(~A)=A
(2)幂等律 A∪A=A,A∩A=A
(3)交换律 A∪B=B∪A,A∩B=B∩A
(4)结合律 (A∪B)∪C=A∪(B∪C),(A∩B)∩C=A∩(B∩C)
(5)分配律 A∩(B∪C)=(A∩B)∪(A∩C),A∪(B∩C)=(A∪B)∩(A∪C)
(6)吸收律 A∩(A∪B)=A,A∪(A∩B)=A
(7)德摩根律 A−(B∪C)=(A−B)∩(A−C),A−(B∩C)=(A−B)∪(A−C)
~(A∪B)=~A∩~B,~(A∩B)=~A∪~B
~E=,~=E
(8)同一律 A∩E=A,A∪=A;
(9)零律 A∩=,A∪E=E
(10)排中律 A∪~A=E
(11)矛盾律 A∩~A=
定理3.7 设A, B, C是任意集合,则
(1)A A∪B,B A∪B
(2)A∩B A,A∩B B
(3)A−B=A∩~B
(4)A−B A
(5)(A−B)∪B =A∪B,(A∪B)−B =A−B
(6)若A C,B C,则A∪B C
(7)若A B,A C,则A B∩C
(8)若A B,则 ~B ~A
定理3.8 对于任意集合A,B,C,
(1)AB=(A−B)∪(B−A)=(A∪B)−(A∩B)
(2)AB=BA
(3)AA=
(4)A=A
(5)~A~B=AB
(6)(AB)C=A(BC)
集合证明题
证明方法:命题演算法、等式置换法
命题演算证明法的书写规范 (以下的X和Y代表集合公式)
(1) 证XY
任取x, xX … xY
(2) 证X=Y
方法一 分别证明 XY 和 YX
方法二
任取x,xX … xY
注意:在使用方法二的格式时,必须保证每步推理都是充分必要的

(1) 判断元素a与集合A的隶属关系是否成立基本方法:
把 a 作为整体检查它在A中是否出现,注意这里的 a 可
能是集合表达式.
(2) 判断AB的四种方法
若A,B是用枚举方式定义的,依次检查A的每个元素是否在B中出现.
若A,B是谓词法定义的,且A, B中元素性质分别为P和Q, 那么"若P则Q"意味 AB,"P当且仅当Q"意味A=B.
通过集合运算判断AB,即AB = B, AB = A, AB = 三个等式中有一个为真.
通过文氏图判断集合的包含(注意这里是判断,而不是证明
求解集合等式成立的充分必要条件可能用到集合的算律、不同集合之间的包含关系、以及文氏图等. 具体求解过程说明如下:
(1) 化简给定的集合等式
(2) 求解方法如下:
- 利用已知的算律或者充分必要条件进行判断
- 先求必要条件,然后验证充分性
- 利用文氏图的直观性找出相关的条件,再利用集合论的证明方法加以验证
证明集合恒等式的方法有两种:
(1)根据定义进行证明,在叙述中采用半形式化的方法,证明中大量用到数理逻辑的等价式及推理规则。

(2)恒等演算,利用已有的集合恒等式证明新的恒等式.

最后
以上就是怡然花瓣最近收集整理的关于离散数学-6 集合代数的全部内容,更多相关离散数学-6内容请搜索靠谱客的其他文章。








发表评论 取消回复