本节主要讲凸集的概念以及保凸运算,这对于判断优化问题是否是凸的非常有帮助。这一节有一部分概念比较抽象,需要仔细研读。
凸集(Convex Set)
凸集
通过集合的任意两个点的线段还在集合中,即

仿射集(Affine Set)
通过集合的任意两个点的直线还在集合中

线性方程组的解集是一个仿射集。
凸组合(Convex Combination)
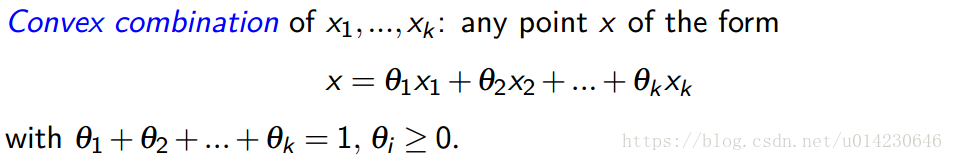
凸包(Convex Hull)
S的凸包是指S中所有点的凸组合组成的集合,凸包是包含S的最小的凸集。
锥(Cones)
锥组合Conic combination
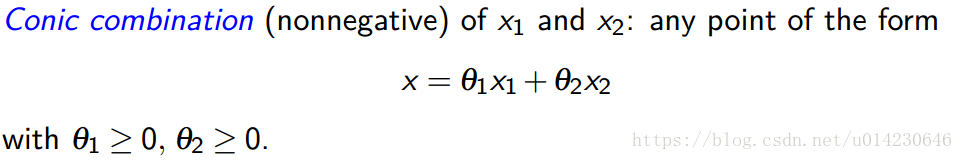
是非负线性组合。
凸锥Convex Conic
任意两个点的锥组合还在集合中。
锥包Conic Hull
集合C的锥包是指C中所有元素的锥组合的集合
保凸运算
通过保凸运算,可以从凸集构造出其他凸集。
如何证明集合C的凸性?
有两种方法:
1.通过定义证明;
2.说明集合C可以通过一些简单的凸集(超平面,半空间,球,椭球,范数球,范数锥,多面体,半正定锥)通过保凸运算导出。
保凸运算包括:
- 取交集
- 仿射函数
- 透视函数
- 线性分式函数
取交集(Intersection)
任意凸集的交集都是凸集
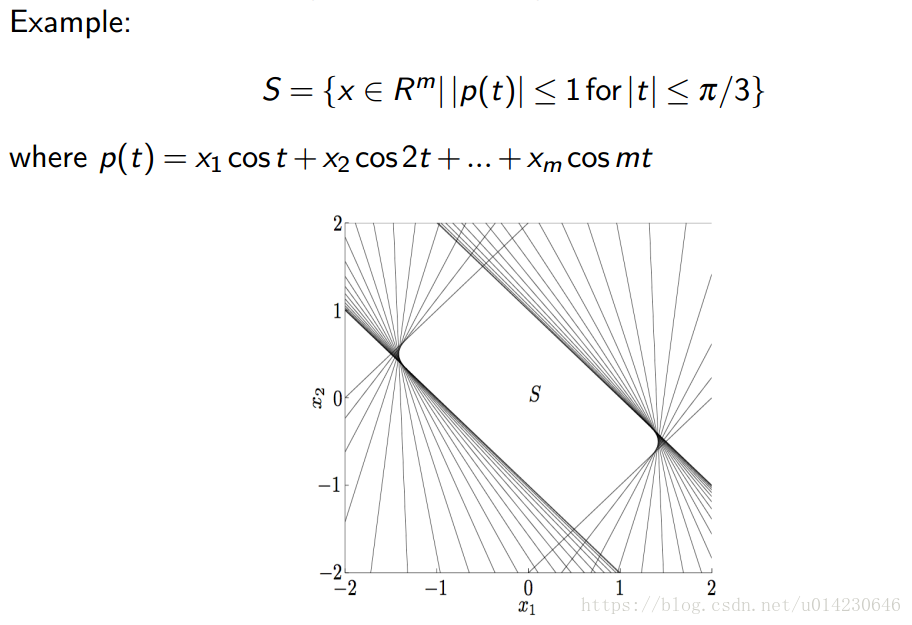
上图的集合是凸集,因为p(t)关于x是线性函数,线性不等式的解集是凸集,要求对不同的t值成立,相当于取交集。所以S是凸集。
仿射函数(Affine Function)
设f是仿射函数,则凸集在f下的像以及原像都是凸的。
仿射函数具有形式: f(x)=Ax+b f ( x ) = A x + b
仿射函数包括:缩放、平移、投影
透视和线性分式函数(Perspective and Linear-fractional Function)
透视函数把向量的最后一维归一化为1,然后丢掉它。形式化地表达如下:
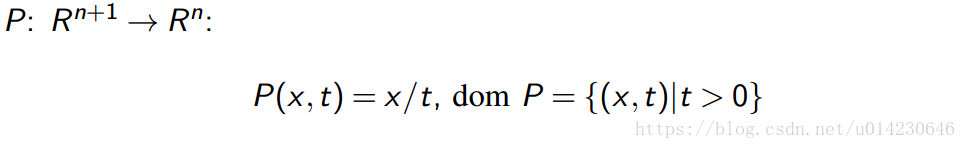
凸集的像和原像在透视变换下都是凸的。
仿射函数和透视函数都属于线性分式函数。线性分式函数可以看成是仿射函数和投射函数的合成。
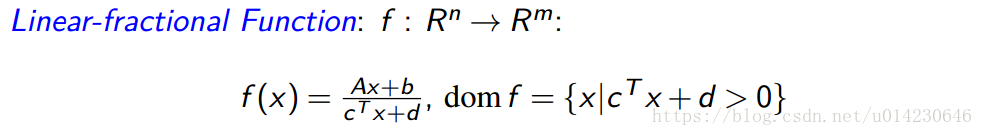
投射解释 线性分式函数可以看成一个矩阵
作用于点(x,1),得到 (Ax+b,cTx+d) ( A x + b , c T x + d ) ,再作归一化使得最后一个分量是1,得到 (f(x),1) ( f ( x ) , 1 )
条件概率
条件概率可以看成是通过线性分式映射得到
广义不等式(Generalized Inequalities)
称锥 K⊆Rn K ⊆ R n 为正常锥(Proper Cones),如果满足:
- K是凸的
- K是闭的
- K是实的,即有非空内部
- K是尖的,即不包含直线
正常锥K可用来定义广义不等式
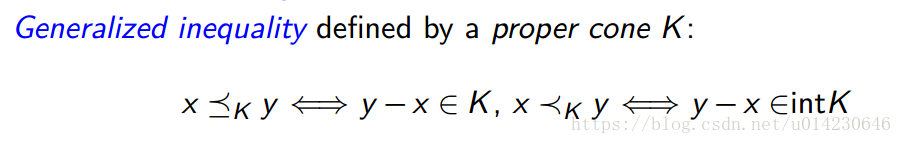
当 K=R+ K = R + 时,偏序关系 ⪯K ⪯ K 即为通常意义上的序 ≤ ≤ 。
非负象限及分量不等式
非负象限是一个正常锥,相应的广义不等式 ⪯K ⪯ K 对应于向量不等式。
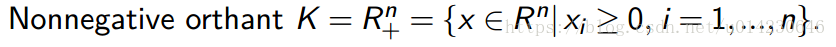
半正定锥和矩阵不等式
半正定锥 Sn S n 是正常锥,相应的广义不等式就是通常的矩阵不等式。即 X⪯KY X ⪯ K Y 等价于 Y−X Y − X 是半正定矩阵。对 Sn+ S + n 有相似结论。
[0,1]上的非负的多项式锥
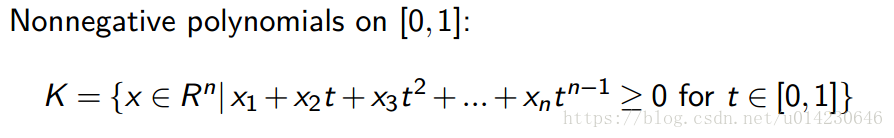
广义不等式的性质
传递性、自反、反对称等,类似于我们常见的不等式。
最小与极小元
广义不等式的一些性质与普通不等式有明显的区别,即对于R上的线性序,任意两点都是可比的,而这个性质对其他广义不等式并不成立。这导致了最大最小的概念在广义不等式下有一些不同。
最小元
可以直观理解成比集合中的每个元素都小( ⪯K ⪯ K )。形式化定义是
极小元
可以直观理解成集合中没有比它更小的元素。形式化定义是
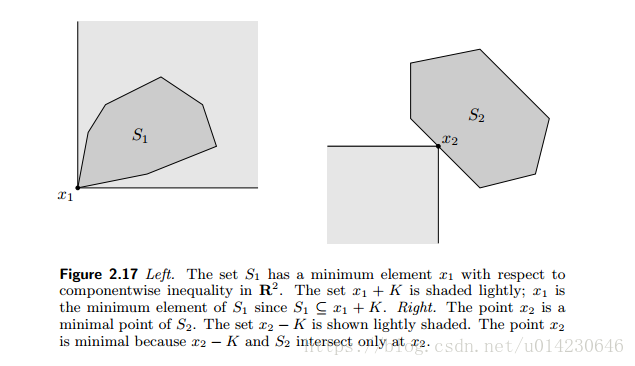
极小元有多个。
分离与支撑超平面
超平面分离定理
两个不想交的凸集C和D,存在一个超平面 aTx≤b a T x ≤ b ,把他们分离开。即对于集合D中所有元素非负,对于集合C中所有元素非正。

严格分离
不相交的凸集并不一定能被超平面严格分离,即使集合是闭集。
点和凸集的严格分离 如果C是闭凸集,而 x0∉C x 0 ∉ C ,那么存在将 x0 x 0 和 C C 严格分离的超平面。
超平面分离定理的逆定理
任何两个凸集,至少一个是开集,当且仅当存在分离超平面时,它们不相交。
支撑超平面定理
若是集合 C⊆Rn C ⊆ R n 的边界 bd C b d C 的一点,即
如果 aTx≤aTx0 a T x ≤ a T x 0 对集合中的任何一点 x x 且,则 {x|aTx=aTx0} { x | a T x = a T x 0 } 是集合C在点 x0 x 0 处的支撑超平面。
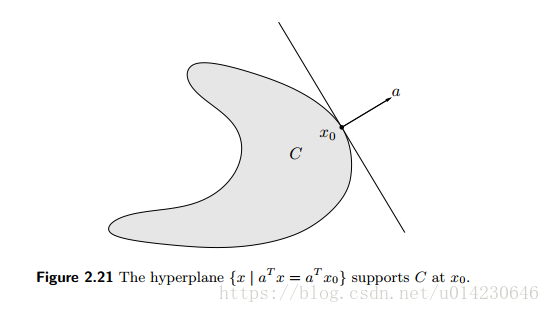
支撑超平面定理:对任意的非空凸集,在边界处存在支撑超平面。
逆定理:集合是闭的,并且有非空的内部,并且其边界上的每个点都存在支撑超平面,那么它是凸的。
对偶锥和广义不等式(Dual Cones and Generalized Inequalities)
对偶锥
令 K K 是一个锥,集合称为 K K 的对偶锥。是一个锥,并且总是凸的,即使 K K 不是凸锥。
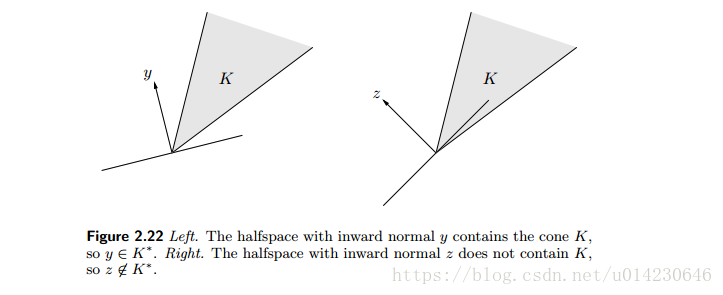
从几何上看,当且仅当是 K K 在原点的一个支撑超平面的法线的反向。
仔细分析,对偶锥是这样的一个区域。区域中的每个点与中的每个点的夹角小于等于90°。 K∗ K ∗ 的边界分别与 K K 的边界垂直。
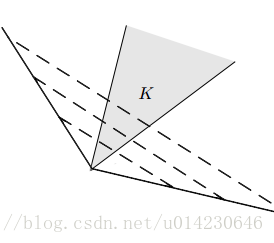
常见对偶锥的例子:
- 非负象限。锥的对偶锥是它本身。称为自对偶。
- 半正定锥。 Sn+ S + n 也是自对偶的
- 范数锥的对偶:
对偶锥满足的性质:
如果 K K 是一个正常锥,那么它的对偶也是正常锥。。
K∗ K ∗ 是指 K K 的凸包和闭包,如果是凸和闭的,那么 K∗∗=K K ∗ ∗ = K 。
广义不等式的对偶(Dual Generalized Inequalities)
因为正常锥的对偶也是正常锥,所以可以从正常锥的对偶导出一个广义不等式。称 ⪯K∗ ⪯ K ∗ 为广义不等式 ⪯K ⪯ K 的对偶。
关于广义不等式及其对偶的一些重要性质:
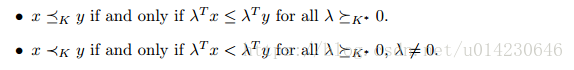
因为 K∗∗=K K ∗ ∗ = K 。
对偶广义不等式的最小元与极小元
待续
参考文献
[1] http://blog.csdn.net/xingce_cs/article/details/73748679
[2]《凸优化》
最后
以上就是羞涩爆米花最近收集整理的关于优化理论(二)凸集、保凸运算、广义不等式与对偶锥凸集(Convex Set)分离与支撑超平面对偶锥和广义不等式(Dual Cones and Generalized Inequalities)参考文献的全部内容,更多相关优化理论(二)凸集、保凸运算、广义不等式与对偶锥凸集(Convex内容请搜索靠谱客的其他文章。








发表评论 取消回复