开环传递函数判断系统类型_第七讲 系统的稳态误差

第七讲 系统的稳态误差

系统的稳态性能反映了系统跟踪控制信号的准确度以及抑制扰动信号的能力，这种能力通常用稳态误差来描述。稳态误差又分为给定值稳态误差（由给定输入引起的稳态误差）和扰动值稳态误差（由扰动输入引起的稳态误差）

7.1 系统的误差及稳态误差的定义

系统的误差e(t)一般定义为被控量的希望值与实际值之差。即

当偏差为零时的实际输出值即为期望值。

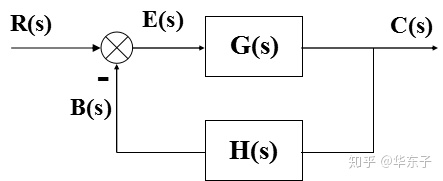
具体来说，对于图所示的反馈控制系统，常用的误差定义有两种

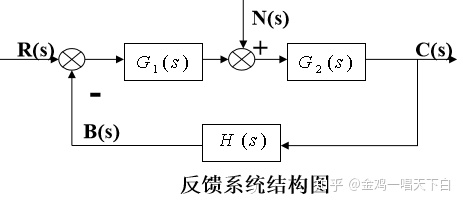
1. 输入端定义

间接定义，参数可测。

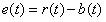
2. 输出端定义

直接定义，参数不可测。

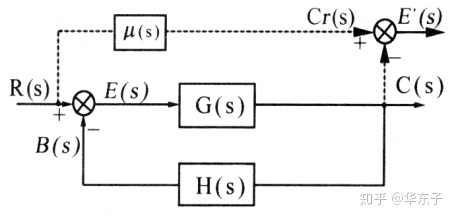
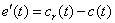
当图中反馈为单位反馈时，即H(s)=1时，上述两种定义可统一为

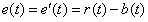
误差响应e(t)与系统输出响应c(t)一样，也包含暂态分量和稳态分量两部分，对于一个稳定系统，暂态分量随着时间的推移逐渐消失，而我们主要关心的是控制系统平稳以后的误差，即系统误差响应的稳态分量——稳态误差记为ess。

定义稳态误差为稳定系统误差响应e(t)的终值。当时间t趋于无穷时，e(t)的极限存在，则稳态误差为

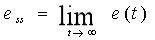
7.2 稳态误差分析

根据误差和稳态误差的定义，系统误差e(t)的象函数

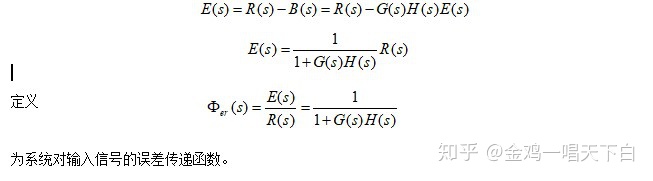
由拉普拉斯变换的终值定理计算稳态误差，则

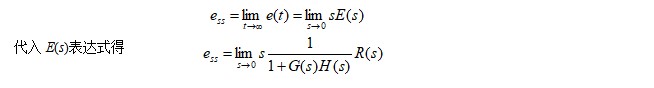
从上式得出两点结论：

1. 稳态误差与系统输入信号r(t)的形式有关；

2. 稳态误差与系统的结构及参数有关。

7.3 稳态误差的计算

对于线性系统，响应具有叠加性，不同输入信号作用于系统产生的误差等于每一个输入信号单独作用时

产生的误差的叠加。

对于图3-7所示系统，输入信号r(t)和扰动信号n(t)同时作用于系统。

1.输入信号r(t)单独作用下， 误差

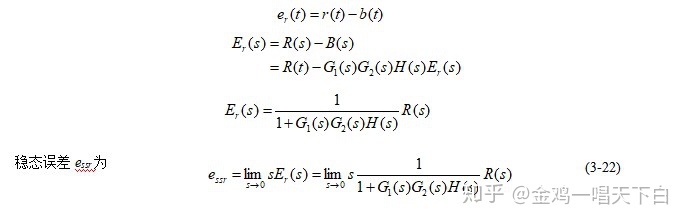
2. 扰动信号单独作用下，误差

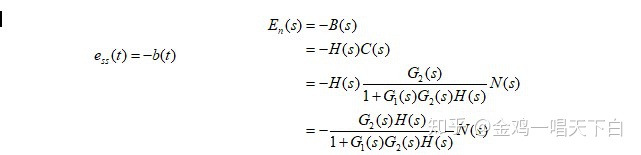
稳态误差

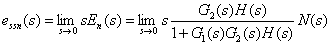
定义

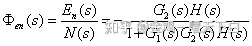
为系统对扰动的误差传递函数。

控制系统在给定信号r(t)和扰动信号n(t)同时作用下的稳态误差ess为

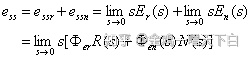
计算表明，稳定误差的大小与系统的放大倍数K有关。即K越大，稳定误差ess越小。要减小稳态误差则应增大倍数K，而稳定性分析却得出，使系统稳定的K只应小于5/4，表明系统的稳态精度和稳态性对放大倍数的要求常是矛盾的。

7.4 应用静态误差系数计算给定信号作用下的稳态误差

7.4.1系统的类型

系统的开环传递函数G(s)H(s)可表示为

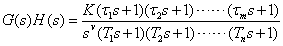
系统常按开环传递函数中所含有的积分环节个数来分类。把

的系统，分别称为0型，Ⅰ型，Ⅱ型，…系统。

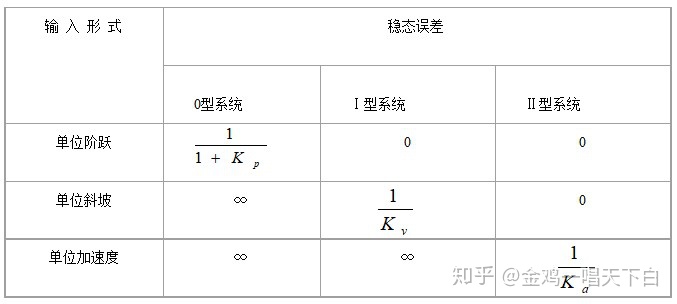
7.4.2 静态位置误差系数Kp

当系统的输入为单位阶跃信号r(t)=1(t)时，由(3-22)式，有

7.4.3 静态速度误差系数Kv

当系统的输入为单位斜坡信号时

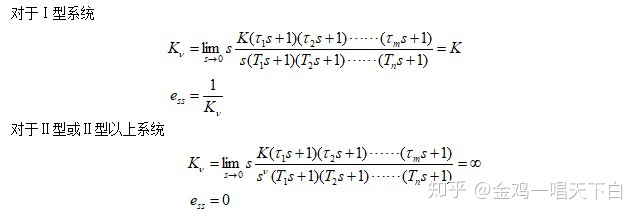
7.4.4静态加速度误差系数Ka

当系统输入为单位加速度信号时，即

其中， ，定义为系统静态加速度误差系数。

对于0型系统，Ka=0，ess=∞；

对于Ⅰ型系统，Ka=0，ess=∞；

对于Ⅱ型系统，Ka=K，；

对于Ⅲ型或Ⅲ型以上系统，

Ka=∞，ess=0 。

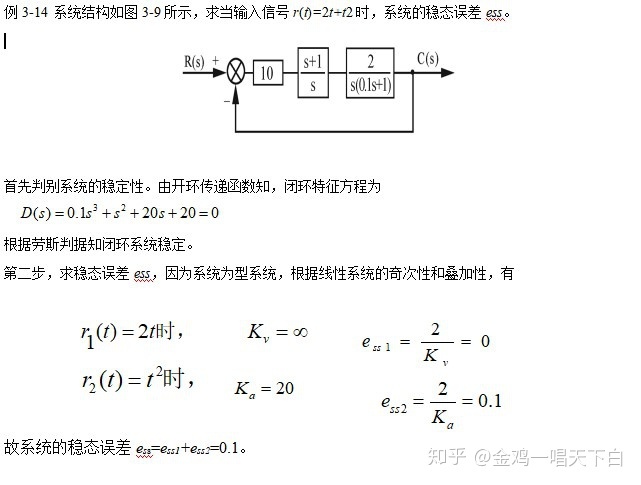
7.5 干扰信号作用下的稳态误差与系统结构的关系

扰动信号n(t)作用下的系统结构图如图

所示

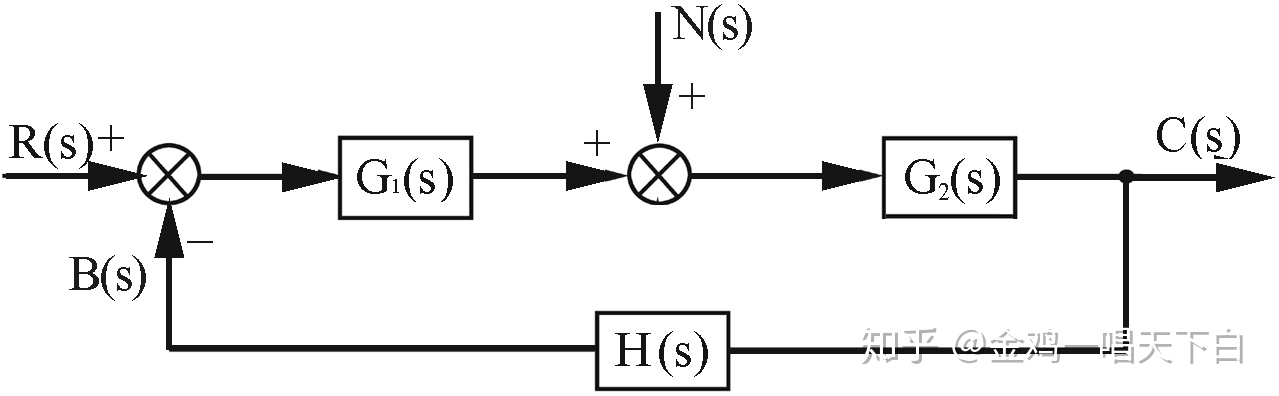
扰动信号n(t)作用下的误差函数为

由上可得，干扰信号作用下产生的稳态误差essn除了与干扰信号的形式有关外，还与干扰作用点之前(干扰点与误差点之间)的传递函数的结构及参数有关，但与干扰作用点之后的传递函数无关。

7.6 改善系统稳态精度的途径

从上面稳态误差分析可知，采用以下途径来改善系统的稳态精度：

＊1. 提高系统的型号或增大系统的开环增益，可以保证系统对给定信号的跟踪能力。但同时带来系统稳定性变差，甚至导致系统不稳定。

＊ 2. 增大误差信号与扰动作用点之间前向通道的开环增益或积分环节的个数，可以降低扰动信号引起的稳态误差。但同样也有稳定性问题。

＊ 3. 采用复合控制，即将反馈控制与扰动信号的前馈或与给定信号的顺馈相结合。

注：版权属笔者所有，如需转载请务必联系！

最后说一句：码字不易，若此文对你有启发，收藏前请点个赞、点点喜欢，是对知乎主莫大的支持！！

参考

1.^文中内容或图片如有侵犯您的权益，请联系作者删除。