• 截止频率是-3dB的频率，两个截止频率之间的频段是带宽
• 0dB处对应的是裕度，是分析稳定性用的。

频率特性和频域稳定判据

频率特性的4种表达形式：

• 频域稳定判据分类：奈氏判据稳定判据和对数频率稳定判据
• 频域稳定判据特点：根据开环系统频率特性曲线判定闭环系统的稳定性。

https://zhuanlan.zhihu.com/p/33007435
https://zhuanlan.zhihu.com/p/400862744

1. 奈氏判据的数学基础

复变函数中的幅角原理是奈氏判据的数学基础，另外，稳定性判定还需选择辅助函数和闭合曲线。

（1） 幅角原理

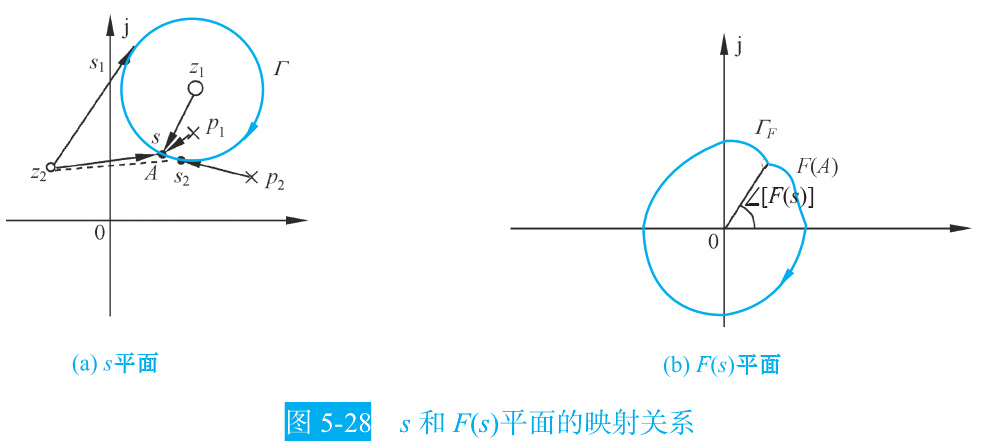
• 幅角原理：设在 s 平面中，闭合曲线 $\Gamma$ 包围函数 F(s)的 Z 个零点和 P 个极点，则 s 沿 $\Gamma$ 顺时针运动一周时，在 F(s)平面上，闭合曲线 ${\Gamma }_F$ 包围原点的圈数 为
  $$R=P-Z$$

• 例子
  

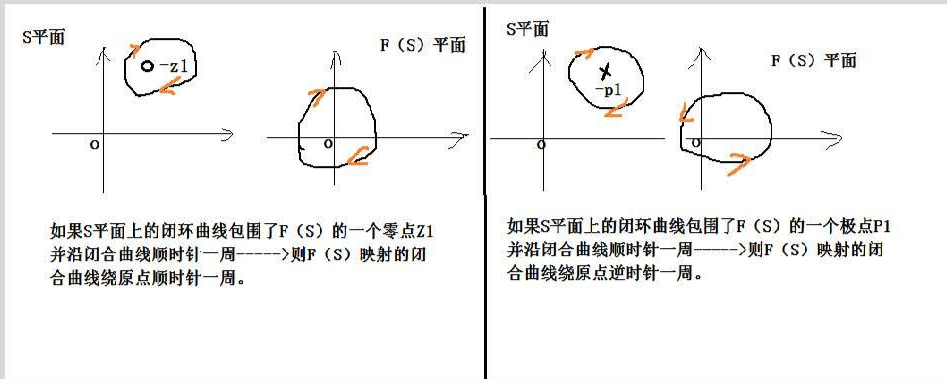
（2） F(s)的选择

F(s)=1+G(s)H(s)

（3） s平面闭合曲线 $\Gamma$ 的选择

系统闭环稳定的条件：系统闭环传函在s的右半平面(图5-28的图(a))无极点 ->
也就是F(s)=1+G(s)H(s)在s的右半平面无零点->
也就是 $\Gamma$ 在右平面无限大时，都不包含零点。->
无限大，就是图5-30(a)，但是需要考虑虚轴上的零极点（为什么书上只考虑了虚轴上的极点了呢？而不考虑虚轴上的零点，难道是因为零点不可能在虚轴上吗？）
为了考虑闭合曲线 $\Gamma$ 应不通过 F(s)的零极点的要求：

1. F(s)无虚轴极点（ F(s)的极点和G(s)H(s)的极点一模一样，因此也可以写为G(s)H(s)无虚轴极点）
2. G(s)H(s)有虚轴极点
   

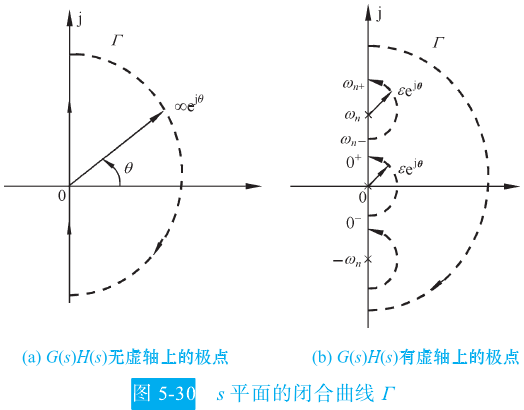
（4）G(s)H(s)闭合曲线的绘制

由上文的(3)可知，s平面中，$\Gamma$ 关于实轴对称。因此，${\Gamma }_{GH}$ 也关于实轴对称。因此，只需要画出${\Gamma }_{GH}$ 虚轴及以上的部分就行。
一下就介绍如何将s平面映射到F(s)平面：

1. G(s)H(s)无虚轴极点

2. G(s)H(s)有虚轴极点

2. 奈氏判据

系统稳定的条件：

1. F(s)=1+G(s)H(s)在s的右半平面(图5-28的图(a))无零点。
   也就是说 $\Gamma$ 需要只包围极点，不包围零点。
2. 那么就是s平面中，$\Gamma$ 包围F(s)的极点数P= F(s)平面的F(s)函数，就是${\Gamma }_F$ 逆时针包围原点的圈数R （R=P）
3. 那么对应开环传函的话：s平面中，$\Gamma$ 包围F(s)的极点数P= F(s)平面的G(s)H(s)函数，就是${\Gamma }_{GH}$ 逆时针包围(-1，j0)的圈数R （R=P）

例5-8的拓展

根据例5-10题目中已知的知识

1. 开环系统稳定，P=0
2. 由开环幅相特性曲线知ν =0，不需补作虚直线。

最后

以上就是饱满书包为你收集整理的【自动控制原理】-奈氏判据频率特性和频域稳定判据的全部内容，希望文章能够帮你解决【自动控制原理】-奈氏判据频率特性和频域稳定判据所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。