概述
系列文章目录
文章目录
- 系列文章目录
- 前言
- 一、特征函数F(s)
- 二、奈奎斯特稳定判据
- 1.映射原理
- 2.应用步骤
- 3.求N的巧妙方法
- 三、系统的相对稳定性
- 1.相角裕量γ
- 2.幅值裕量 K g K_g Kg
前言
Nyquist判据是判断系统稳定性的图解法判据
一、特征函数F(s)
闭环传递函数
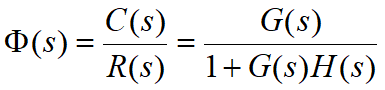
系统特征函数
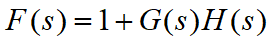
F
(
s
)
F(s)
F(s)的零点就是闭环极点
F
(
s
)
F(s)
F(s)的极点就是开环极点
通过
F
(
s
)
F(s)
F(s) 把开环极点与闭环极点联系起来，由开环极点来判别未知闭环极点
二、奈奎斯特稳定判据
1.映射原理
N
=
P
−
Z
N=P-Z
N=P−Z
N
N
N:
G
H
GH
GH曲线在
G
H
GH
GH平面绕（-1，j0）逆时针转的圈数
P
P
P：开环右极点数
Z
Z
Z：闭环右极点数
2.应用步骤
（1）由开环传递函数确定p,v,n-m
p:开环右极点数
v:开环积分环节数
n-m:分母的次数-分子的次数
（2）绘出
G
(
j
ω
)
H
(
j
ω
)
G(jω)H(jω)
G(jω)H(jω)极坐标图（
ω
=
0
+
−
>
ω
=
∞
ω=0^+->ω=infty
ω=0+−>ω=∞）
(3)按照镜像原则绘出
ω
=
−
∞
−
>
ω
=
0
−
ω=-infty->ω=0^-
ω=−∞−>ω=0−
(4)从
G
H
GH
GH的
ω
=
0
−
ω=0^-
ω=0−起，顺时针增补模为无穷大，角度从
+
v
9
0
0
+v90^0
+v900到
−
v
9
0
0
-v90^0
−v900的圆弧
(5)求
N
,
P
,
Z
N,P,Z
N,P,Z判稳定。若
Z
=
0
Z=0
Z=0,闭环系统稳定
3.求N的巧妙方法
当
G
(
j
ω
)
H
(
j
ω
)
G(jω)H(jω)
G(jω)H(jω)曲线的形状较复杂, N 不易找准时,常利用穿越概念求 N 。
G
(
j
ω
)
H
(
j
ω
)
G(jω)H(jω)
G(jω)H(jω)在 (-1, j0)点以左穿过负实轴时，称穿越
正穿越a：从负实轴上方到下方
负穿越b：从负实轴下方到上方
N
=
a
−
b
N=a-b
N=a−b
三、系统的相对稳定性
1.相角裕量γ
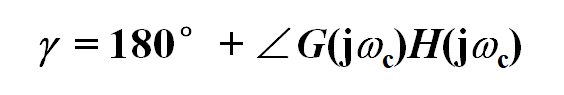
ω
c
ω_c
ωc:幅值穿越频率，此时
G
(
j
ω
)
H
(
j
ω
)
G(jω)H(jω)
G(jω)H(jω)幅值等于1
2.幅值裕量 K g K_g Kg
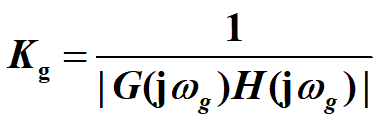
ω g ω_g ωg:相位穿越频率，此时 G ( j ω ) H ( j ω ) G(jω)H(jω) G(jω)H(jω)相角等于-180
最后
以上就是无奈奇异果为你收集整理的自动控制理论（9）——奈奎斯特稳定判据系列文章目录前言一、特征函数F(s)二、奈奎斯特稳定判据三、系统的相对稳定性的全部内容，希望文章能够帮你解决自动控制理论（9）——奈奎斯特稳定判据系列文章目录前言一、特征函数F(s)二、奈奎斯特稳定判据三、系统的相对稳定性所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复