对奈奎斯特稳定判据的理解

设系统的开环传递函数为$G(s)H(s)$,引入辅助函数

$$F(s)=1+G(s)H(s)=1+\frac{M(s)}{N(s)}=\frac{N(s)+M(s)}{N(s)}(1)$$
由（1）式可知，辅助函数$F(s)$的分子与分母多项式的阶次是相同的，$F(s)$的零点就是系统闭环传递函数的极点，$F(s)$的极点就是开环传递函数的极点，我们知道，系统稳定的充分必要条件是系统闭环传递函数的极点全部位于S平面的左半平面，因此判定系统稳定性的问题就可以化为寻找$F(s)$的零点分布问题。前人提出的方案是寻找$F(s)$在右半平面的零点数。
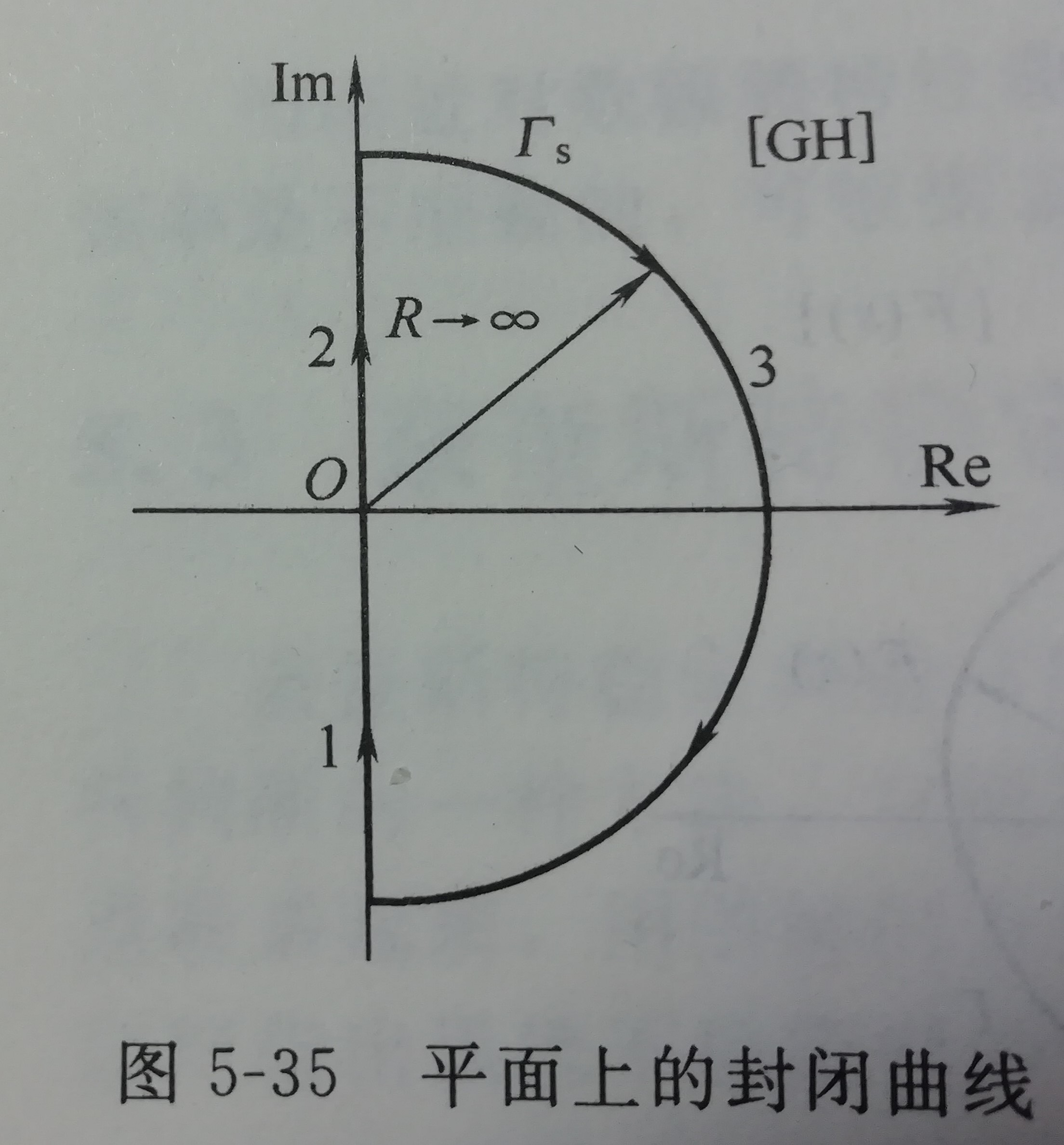
为此我们画出一个半径无穷大的（如图1），直径在虚轴上，圆弧是在右半平面的顺时针方向的圆，该圆足以包含$F(s)$的所有在右半平面的零点(如果有的话)，我们称该顺时针圆为奈奎斯特路径，马上，$F(s)$中的S将绕该路径一圈

设$F(s)$在右半平面的极点数为$N_p$，零点数为$N_z$，

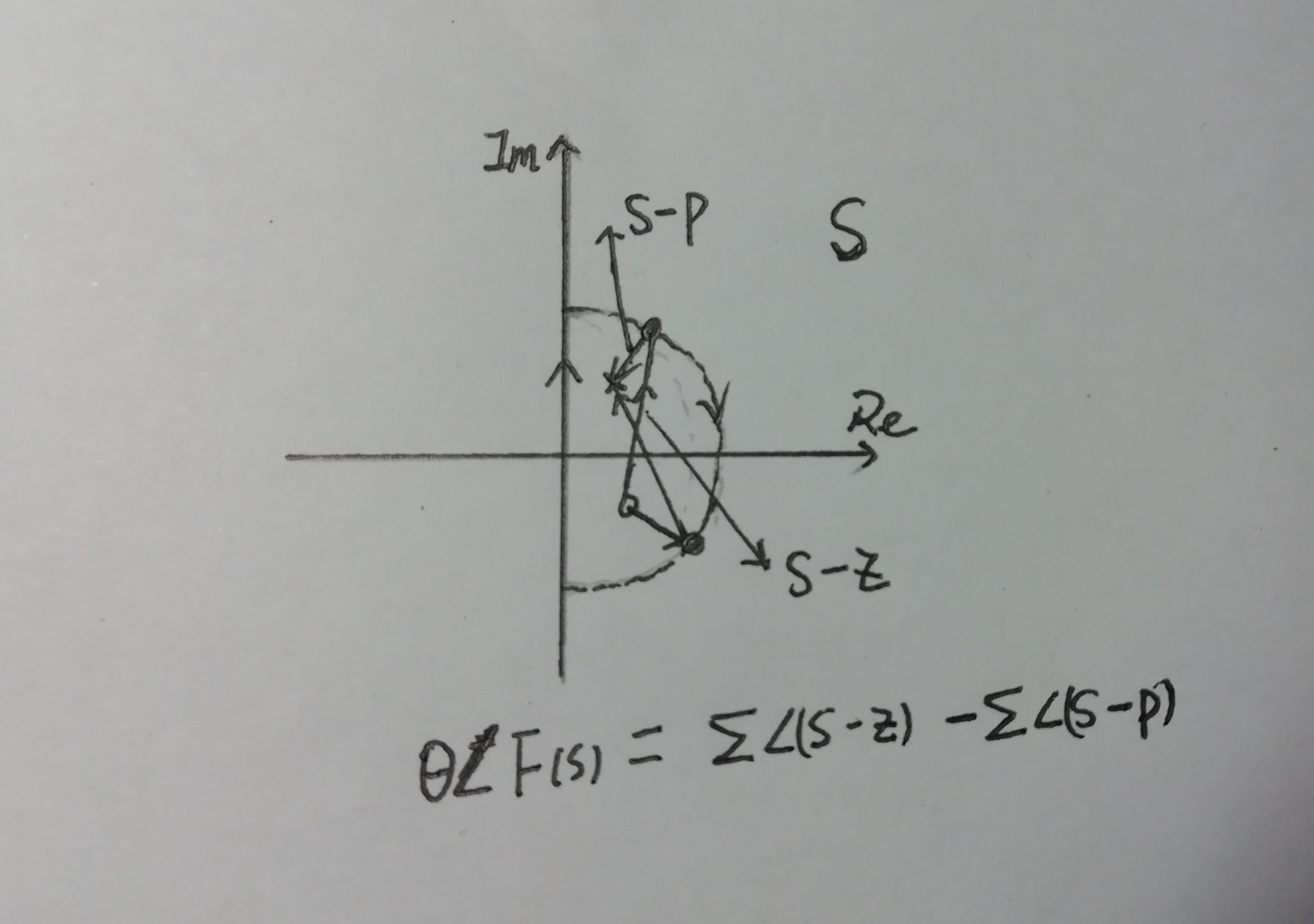
由图2，根据对图2的理解我们看出当S绕奈奎斯特路径一圈时，如果$F(s)$在圆内有一个零点，那么F(s)将会绕着原点逆时针一圈，如果$F(s)$在圆内有一个极点，那么$F(s)$将会绕着原点顺时针一圈，所以$F(s)$绕原点的角度就可以表示为$-2\pi (N_z-N_p)$，我们知道系统稳定的充要条件在现在是$N_z=0$，也就是说$F(s)$逆时针绕原点的圈数要等于$N_p$，系统才会稳定，我们知道$F(s)$逆时针绕原点的圈数也就等价于$G(s)H(s)$绕$(-1,j0)$的圈数。
综上所述，系统稳定的充要条件是：当S绕奈奎斯特路径一圈后，系统开环传递函数绕$(-1,j0)$的圈数要等于该开环传递函数在右半平面的极点数。
感谢阅读，不对之处请指正，通俗的理解，没有严格的数学证明，望见谅。

最后

以上就是粗暴盼望为你收集整理的对奈奎斯特稳定判据的理解的全部内容，希望文章能够帮你解决对奈奎斯特稳定判据的理解所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。