频域分析之对数频率稳定判据

由之前的博客 奈奎斯特稳定性判据的推导 可知，奈奎斯特稳定性判据的关键是根据开环频率特性曲线(奈奎斯特曲线/幅相特性曲线)来确定穿越次数$N$,即$G(jw)H(jw)$曲线逆时针包围$-1+j0$点的次数；而所谓对数频率稳定判据，就是将奈奎斯特稳定性判据由奈奎斯特图推广到波德图上；

奈奎斯特曲线(幅相特性曲线)对$-1+j0$点之左侧实轴的穿越(注意，只有对左侧实轴的穿越能形成对对$-1+j0$点的包线，该点右侧的穿越为无效穿越)等价于：波德图中，相频特性曲线对$\varphi =-180^{\circ }$线的穿越。同样的，定义相角增大的穿越为正穿越，相角减小的穿越为负穿越。

由此引出系统的对数频率稳定判据：系统的闭环右极点数为$Z=P-2N$，$N$是相频特性曲线对$\varphi =-180^{\circ }$线的穿越次数，若$Z=0$系统闭环稳定，否则系统闭环不稳定。

同样的，与奈奎斯特稳定性判据相同，对数频率稳定判据也需要考虑半次穿越和画补线的问题，当系统的开环传递函数型别不为0时，需要画出补线(从零频率对应的相角处，沿相角增大方向，补$v90^{\circ }$的补线即可)

例：

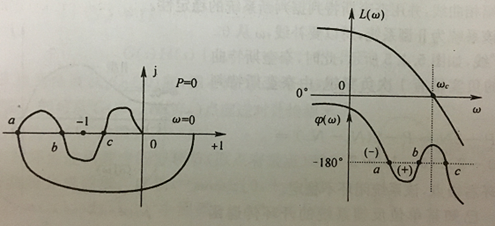
如上图所示，

奈奎斯特曲线对$-1+j0$点之右侧实轴的穿越为无效穿越，对应幅相特性曲线中对穿越频率之右的穿越(穿越频率对应幅值为1的频率值，在奈奎斯特曲线中做圆心在原点，半径为1的单位圆，很容易看出：对$-1+j0$点之右侧实轴的穿越对应的频率要大于穿越频率)，故c点为无效穿越。

$$Z=P-2N=P-2\left(N_{+}-N_{-}\right)=0-2\times (1-1)=0$$

系统闭环稳定。

又如系统：

$$G(s)=\frac{K\left(\frac{1}{3}s+1\right)}{s(s-1)}$$

其波德图(幅相特性曲线)如下：

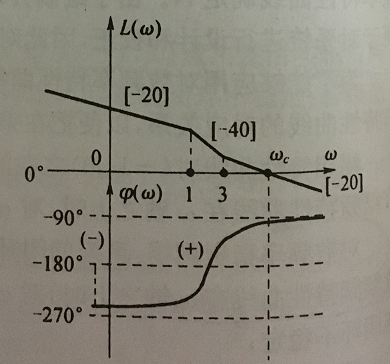
其为1型系统，在零频率对应相角处补$90^{\circ }$的补线(画成实轴的垂线即可)；

其相频特性曲线对应半次负穿越和一次正穿越；则根据对数频率稳定判据：

$$Z=P-2N=1-2\left(N_{+}-N_{-}\right)=1-2\times \left(1-\frac{1}{2}\right)=0$$

系统闭环稳定，可见当系统含有不稳定环节(或非最小相位环节)时，系统也可能闭环稳定

最后

以上就是敏感大门为你收集整理的频域分析之对数频率稳定判据的全部内容，希望文章能够帮你解决频域分析之对数频率稳定判据所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。