超前 、滞后、超前滞后介绍

作者：不足为外人道也
链接：https://www.zhihu.com/question/38726841/answer/495410998
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
 

一、先以超前校正为例：

1、目的

要在改善动态性能的同时，保证静态性能基本不变

2、手段

根轨迹和波特图分别在时域和频域上包含了系统的全部结构信息，因此改善动态/静态性能等于“操纵”根轨迹和波特图

改变开环增益K是最容易的，但是当系统结构确定的时候，K值的能力范围有限：

（1）体现在根轨迹上，K值只能让根落在属于根轨迹的位置，若指标要求在其他位置，K无能为力

（2）体现在波特图上，K值对相频特性没有影响，对幅频特性只能影响它的上下位置，而不能改变它的“形状”（就是它在哪转折怎么转折）

这些都是因为，根轨迹、波特图“形状”都是由系统结构决定的，想改变它们，当然要从系统结构入手，系统结构指的就是方块图上积分装置的数量和反馈深度（这自然是废话……不过刚接触控制理论的时候要意识到这些概念也不太容易）

3、实现：

（1）若用根轨迹（时域法）

那么手段就是改变根轨迹的走向使其路过满足性能要求的区域，具体怎么改变 @花满楼 说的很细致了，我不严谨地总结一下：

先引入新零点把根轨迹往目的区域“拉”，然后加入新极点弥补零点引入带来的问题。

或者换一个角度来讲，超前校正引入的零点和极点，二者的距离不会太远（或者说一定程度上相对来说不太远），这种距离很近的零极点组合，有个很形象的名字：偶极子（偶极子的概念应该有很多学科都在用，比如大物上讲正负点电荷电场分布的时候……）。

偶极子特点是：它们的影响只局限于它们附近的区域，在复平面远区 ，二者的影响被相互抵消了（这个从表达式上很容易看出来），这带来一个好处：

可以相对来说较为精确地对某一范围进行操作而不至于对其他地方产生过大的影响。

观察@花满楼 提供的引入校正前后的根轨迹，可以看到偶极子近区的根轨迹分布有了很大的改变，而离它很远的地方的根轨迹走向变化并不特别明显。（不知道这样说对不对）

超前校正的两个参数T和α，前者决定这对偶极子的位置，后者决定偶极子的距离（也就是对其近区的影响程度），根据需要确定了这两个参数让根轨迹路过满足需要的区域之后，下一步让K取合适的值让闭环极点落在那个区域之内即可收工。

（2）若用波特图（频域法）

那么想做的就是把不合理的部分给“折一折”。

把最上面的目的那句话翻译一遍：想改善动态性能，换成这里的话就是“想把中频曲线段往上折”，同时保证静态性能基本不变，换成这里的话就是“低频段的幅频曲线不折 ”。顺手盗下

Kaixiang Wang

的图，若介意评论一下我会删的…

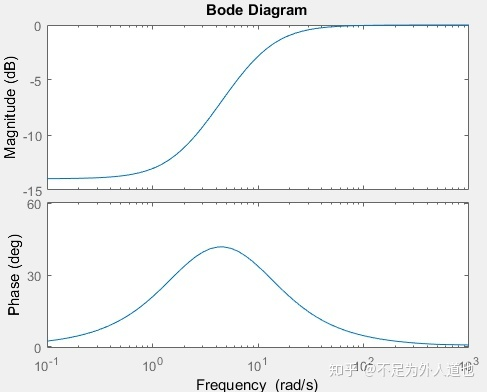
超前校正波特图

正好是把较高的频段往上折，低频段基本保留（注：还是牺牲了更高频段的抗干扰能力），这就是偶极子对幅频曲线分段操作的能力。再看相频特性，由于比例积分和比例微分对相角的影响都是有限的（90度之内），而且二者在远区对相角的影响抵消，所以偶极子能让它附近的相角超前，其他地方的影响不大，这可以算是超前校正在改变动态性能的同时获得的一个“附加的福利”。

相对于K值的调节（即比例调节），能改变幅度不稀奇，稀奇的是既能分段改变幅度又能提高稳定性（相角超前）。

在这里两个参数T和α，前者决定在哪儿分段折高幅频曲线，后者决定折高多少以及同时决定带来多少附加超前角。

二、接着看滞后校正

1、目的

要在改善静态性能的同时，保证动态性能基本不变

2、手段

同样，还是从根轨迹（时域法）和波特图（频域法）两个角度来看。

（1）根轨迹（时域法）

没啥说的，思路和超前校正一样，区别无非是零点和极点谁在左谁在右（偶极子往哪个方向修正根轨迹）而已。同样是确定了T和α之后就确定了根轨迹，然后再调K让极点落在合适的位置。

（2）波特图（频域法）

也是把不符合要求的幅频段“折一折”。

再把目的翻译一遍：想改善静态性能，换成这里的话就是“想把低频段曲线段往上折”，同时保证动态性能基本不变，换成这里的话就是“中高频段的幅频曲线不折 ”。

再盗个图……（罪过罪过）

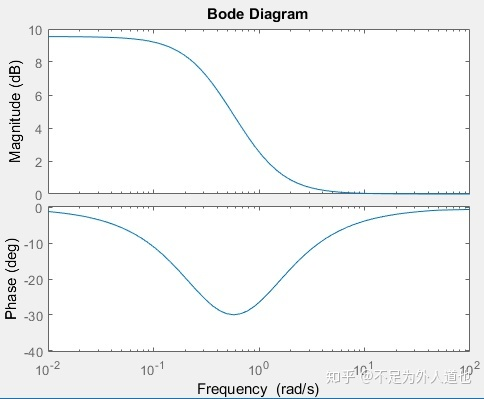
滞后校正波特图

正好是把低频段往上折，中高频段没怎么变，只要两个转折频率（1/T和1/αT）足够小（反正严格上的静态特性（主要是静差）指的是几乎是0的频率分量也就是直流，小点没关系），就可以让对高频区影响很微小。

虽然有副作用——相位引进了滞后角，但没关系，只要转折频率够小，对中高频段的影响就可以控制得很小。

三、滞后-超前校正

1、目的

既改善静态性能，又要改善动态性能。

2、手段

很容易理解，就是把滞后校正和超前校正串联起来，各自在不同频段起作用，优势互补。

3、可能有点多余的东西

（1）比例调节也能既提高静态增益，又提高中频段宽，滞后-超前校正好在哪？

a.比例调节只有一个自由度K，静态性能的改善和动态性能的改善都是同步绑定的，二者很可能相互制约，而滞后-超前校正有3个自由度，可以分别对不同频段进行各自的操作，一个像是“大水漫灌”，另一个是“精耕细作”；

b.比例调节提高增益的同时，是以牺牲系统稳定性为代价的，“稳定压倒一切”，不能随便减小相位裕度，而滞后-超前校正有超前角来补偿相位的滞后，甚至能使系统比以前还要

（2）没图可盗了，只好自己画一个吧：

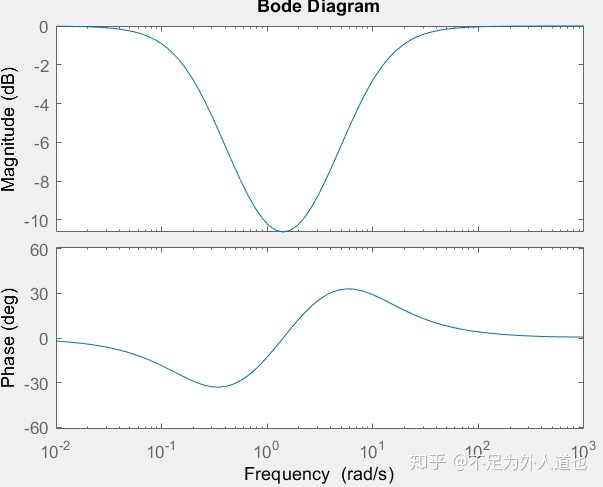
滞后-超前校正波特图

相频曲线上直观地看，像是把低频区不那么重要的相角“挖”了一块“填”到了相角比较重要的中高频段，不赔不赚~

参考资料：

https://blog.csdn.net/weixin_41827761/article/details/90262025

最后

以上就是土豪星星为你收集整理的超前 、滞后、超前滞后介绍的全部内容，希望文章能够帮你解决超前 、滞后、超前滞后介绍所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。